Spring Forces In Parallel, Series And Balance, Illustration, Important Topics For JEE Physics 2024
Shrivastav 11 Mar, 2024
Share
Spring Forces : In mechanics, we come across the system of bodies connected with springs. For this purpose, we need to develop the ideas how exactly a spring responds to an external force applied on it.
First of all, for the sake of simplicity, let us consider a light (massless) spring. Then fix one of its end and pull the other end slowly through a distance x (say). When we go on pulling the end P of the spring towards right, the spring pulls us towards left with a gradually increasing force F . Likewise, when we go on pushing the end P towards left, the spring will push us towards right with a gradually increasing force F .
Spring Forces
The force offered by the spring, that is, "spring force" F points (acts) opposite to the displacement of the force end of the spring. the amount of springs force increase linearly with the deformation (compression or elongation) of the spring; when we plot the variation of F , versus x , we obtain a straight line up to certain (limited) value of x , which is known as elastic limit.
Robert Hooke experimented in seventh century who put forth all the above facts in a single vector formula in scalar form.
Force Stretch (or compression), i.e., F = kx
i.e., restoring force is linear. This force in a spring is not constant and depends on stretch (or compression) x . Greater the stretch (or compression), greater will be the force and vice-versa.
∙ Every spring opposes the attempts to change its length i.e. every spring opposes the phenomenon of compression or extension. This opposing or the resistive force called as the Restoring Force or the spring force F increases with change in length of the spring i.e., Extension or Compression ( x ) . When spring is in its natural length l 0 , spring force ( F sp ) is zero.
Spring force is given by F = – k x , where x is the change in length of the spring (also called as compression or extension) and k is the Spring Constant or Force constant having SI unit Nm –1 and dimensional formula MT –2 . The spring constant k is also known as force constant/spring factor/force factor. The spring constant k depends on geometry of the spring and on the material property. For us, it is important to know that the spring constant is inversely proportional to its natural length l , other things remaining the same i.e.,
{everything else constant}
kl
= constant
Therefore if you cut a spring into two parts whose length are in ratio 1 : 2, their spring constants will be in ratio of 2 : 1. The negative sign in the above relation signifies that the spring force is always directed opposite to the compression or extension in the spring.
As in case of rope, we will usually deal with a massless spring for which the force at each point is the same. Such springs are normally referred to as ideal.
Important Points To Remember Related Spring Forces
(a) For a spring of natural length l , spring constant k , we have, kl = constant
(b) No need to take the negative sign as the direction has already been taken.
(c) The more the value of k , the more the elastic a spring is.
(d) Soft springs have small k in comparison to hard spring e.g., Spring used in a ball pen (soft spring). Spring used in the shocker of the car (hard spring).
(e) The graph showing variation of restoring force F with extension/compression x is shown here.
(h)
If springs of spring constants
k
1
,
k
2
,
k
3
… are connected in parallel, then effective spring constant.
k
eff
=
k
1
+
k
2
+
k
3
+ …
(i)
SI unit of
k
is Nm
–1
and [
k
] =
MT
–2
.
(j)
When a spring is cut, then to calculate the force constant of each divided part we have
Spring Forces Illustration
Spring Forces Illustration : A spring of force constant k and natural length l is cut into two parts of lengths l /3 and 2 l /3. Find the new force constant of the divided parts.
Ans. Since, kl = constant
Forces Constant Of Composite Springs Forces
If a number of springs are connected to a body and we want to produce it to a single spring. Following three cases of common interest are possible.
Springs Forces In Parallel
Springs Forces In Parallel : This situation is shown in figure. If the force F pulls the mass m by y , the stretch in each spring will be y , i.e., y 1 = y 2 = y …(i)
but for equilibrium,
[as
F
=
ky
]
Which in the light of (i) reduces to
k = k 1 + k 2 + …
This is like capacitors in parallel or resistance in series.Springs Forces In Series
Springs Forces In Series : This situation is shown in figure.
But,
or
[as for
y
= (
F
/
k
)]
Which in the light of Eq. (i) reduces to
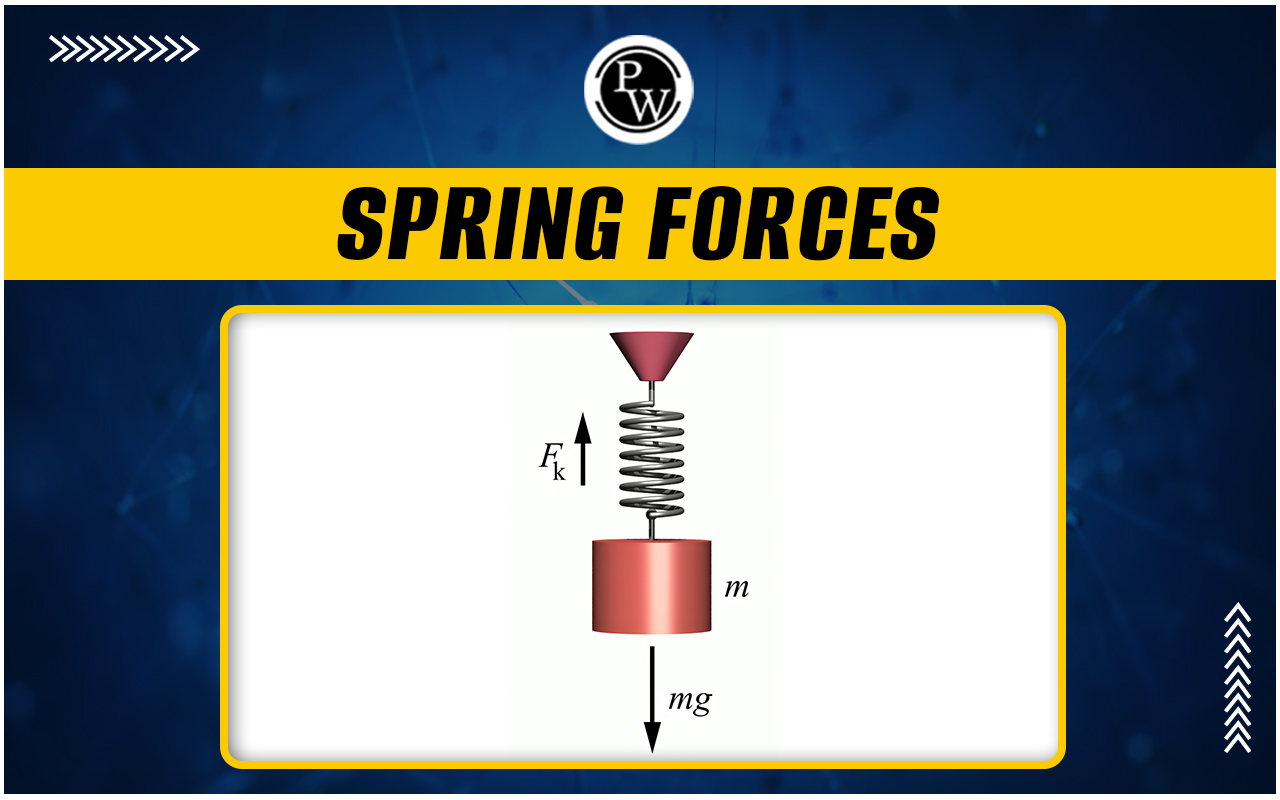
Spring Forces Balance
Spring Forces Balance : A spring balance does not measure the weight. It measures the force exerted by the object at the hook. Symbolically, it is represented as shown in figure. A block of mass m is suspended at hook.
When spring balance is in equilibrium, we draw the F.B.D. of mass m for calculating the reading of balance. Unless and until mentioned, a spring balance is assumed to be light or having negligible mass.
T
=
mg
Magnitude of
T
gives the reading of spring balance.
Spring Forces FAQs
Q. 1: What is Hooke’s law?
Q.2: What is work done by a spring force?
Q.3 : More the value of k, _________ elastic the spring is.
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
