Physics Wallah

Normal Force Formula - Definition, Equation, Examples

Normal Force Formula (N) (F= ma)  is a fundamental concept in physics, representing the force exerted by a surface to support the weight of an object in contact with it, acting perpendicular to the surface.
authorImageMurtaza Mushtaq6 Oct, 2023
Share

Share

Normal Force Formula - Definition, Equation, Examples

What is Normal Force?

In Normal force Formula, often denoted as N, is a fundamental concept in physics that arises when two objects are in contact with each other. It is the force exerted by a surface to support the weight of an object resting on it. The term "normal" refers to direction perpendicular to the surface .

Normal Forces on a Flat Surface

In Normal force Formula,When an object rests on a flat surface, the normal force acts vertically upward, opposing the force of gravity. This ensures that the object remains in a state of equilibrium, neither sinking into the surface nor accelerating upward.

Normal Force Equation

The normal force can be calculated using the following equation: N = mg

Where:

- N is the normal force. - m is the mass of the object. - g is the acceleration due to gravity (approximately 9.81 m/s² on Earth).

Also Check - Gravitation Force Formula

This equation simplifies the understanding of normal force, as it depends solely on the object's mass and the gravitational acceleration.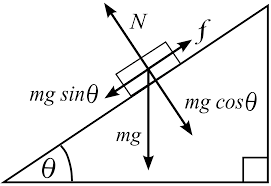

Normal Force Formula Examples

Let's explore some real-world examples to better grasp the concept of normal force: Example 1: A Book on a Table Imagine placing a book on a table. The normal force acts upward, counteracting the book's weight, keeping it from falling through the table. Example 2: A Person Standing When a person stands on the ground, the normal force exerted by the ground prevents them from sinking into the Earth due to gravity. Example 3: Car Tires on the Road In the case of a car, the normal force between the tires and the road surface provides the necessary traction for driving and braking.

Also Check - Work Done by a Constant Force

Solved Examples on Normal Force

Example 1: A Book on a Table You have a book resting on a table, and you want to calculate the normal force acting on the book.

Solution:

Step 1: Gather the data. - Mass of the book (m): Let's assume the mass of the book is 1.5 kilograms (kg). - Acceleration due to gravity (g): Approximately 9.81 m/s² on Earth. Step 2: Use the Normal Force Equation. The normal force (N) can be calculated using the equation N = mg, where N is the normal force, m is the mass of the book, and g is the gravitational acceleration. Step 3: Calculate the normal force. N = (1.5 kg) × (9.81 m/s²) = 14.715 N So, the normal force acting on the book on the table is approximately 14.715 newtons (N).

Also Check - Work Done by a Variable Force

Example 2: A Person Standing Now, let's consider a person standing on the ground and calculate the normal force exerted by the ground on the person.

Solution:

Step 1: Gather the data. - Mass of the person (m): Let's assume the person's mass is 70 kilograms (kg). - Acceleration due to gravity (g): Approximately 9.81 m/s² on Earth. Step 2: Use the Normal Force Equation. N = mg Step 3: Calculate the normal force. N = (70 kg) × (9.81 m/s²) = 686.7 N So, the normal force exerted by the ground on the person is approximately 686.7 newtons (N). Example 3: Car Tires on the Road In this example, we'll consider a car with a mass of 1200 kilograms (kg) and calculate the normal force acting on its tires when it's parked on a flat road.

Solution:

Step 1: Gather the data. - Mass of the car (m): 1200 kg - Acceleration due to gravity (g): Approximately 9.81 m/s² on Earth. Step 2: Use the Normal Force Equation. N = mg Step 3: Calculate the normal force. N = (1200 kg) × (9.81 m/s²) = 11772 N So, the normal force acting on the car's tires when it's parked on the road is approximately 11772 newtons (N). These examples illustrate how to calculate the normal force using the normal force equation (N = mg) in different scenarios.

Normal Force FormulaFAQs

What happens if the normal force is greater than gravity?

 If the normal force exceeds the force of gravity acting on an object, it will experience an upward acceleration.

Can the normal force be negative?

  No, the normal force is always positive or zero.

Does the normal force change when an object is in motion?

The normal force typically remains constant as long as the object doesn't change its contact with the surface.

Is the normal force the same as weight?

 No, weight is the force of gravity acting on an object, while the normal force is the force exerted by a surface to counteract gravity.

Can there be multiple normal forces acting on an object?

Yes, in scenarios involving inclined surfaces or objects in contact with multiple surfaces, there can be multiple normal forces.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.