
RMO 2025 Paper Analysis: The Regional Mathematical Olympiad (RMO) 2025 has just concluded across various centers on November 16, 2025. As students emerge from the examination halls, the initial discussions are already hinting at the nature of this year's paper.
Our Olympiad Wallah team, along with feedback from students who appeared and teachers, brings you a quick, RMO 2025 Paper Analysis.
Also Read:
RMO 2025 Paper Analysis (Exam Structure)
The RMO 2025 Paper Pattern details are provided below.
| RMO 2025 Paper Analysis | |
| Component | Details |
| Total Questions | 6 |
| Total Marks | 102 |
| Duration | 3 hours |
| Format | Proof + Reasoning-based |
RMO 2025 Paper Analysis: Overall Difficulty Level
-
The RMO 2025 paper was moderately tough, particularly due to
-
substitutions
-
maintaining symmetry
-
dealing with cubic forms
-
Compared to previous years, RMO 2025 felt more concept-heavy
Students who have cleared RMO should gear up—INMO Training Camp is next, with low-cost enrollment mentioned during the live session.
RMO 2025 Questions and Solutions


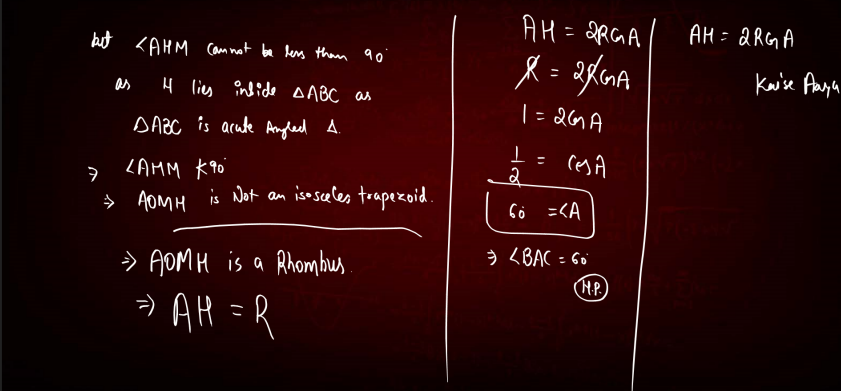
RMO 2025 Paper Analysis: Topic-wise Weightage
1. Number Theory (NT)
Major role through Q3, Q4, Q6.
2. Geometry (G)
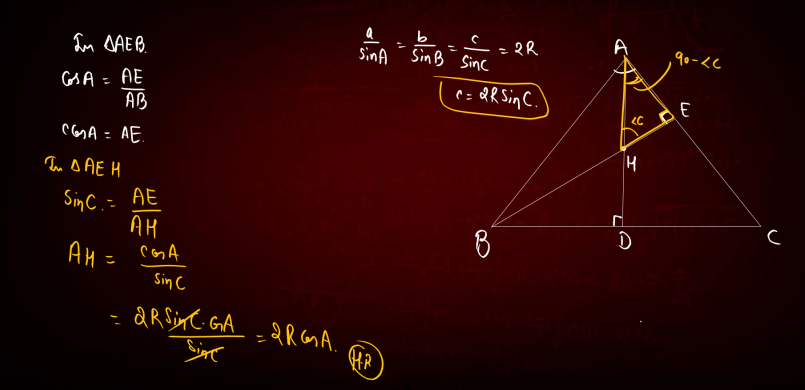
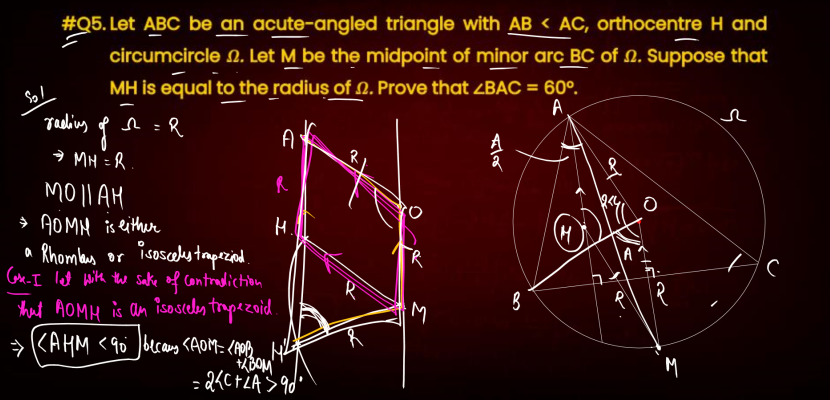
A signature Olympiad geometry problem took center stage in Q5.
3. Algebra (A)
Q2 featured deep algebraic symmetry.
4. Combinatorics (C)
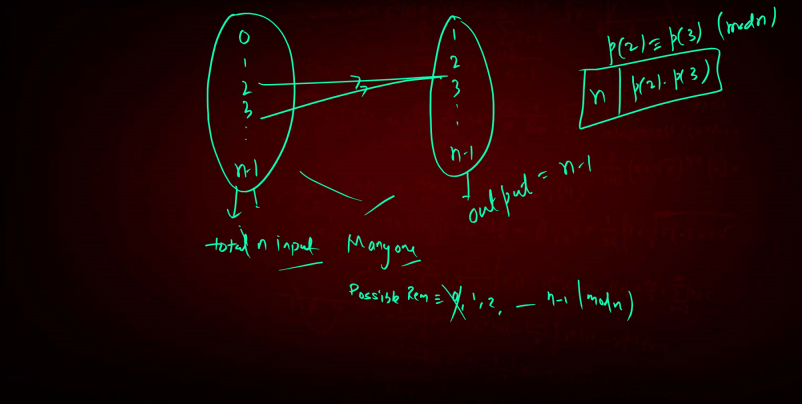
Q1 provided configuration-based combinatorics.
A. Number Theory (NT)
This is usually the highest-scoring area, often featuring 1-2 questions.
-
Focus: Divisibility rules, modular arithmetic (congruences), prime numbers, properties of integers, and Diophantine equations.
-
Tip: RMO questions often involve finding integer solutions or proving divisibility properties using the principle of induction or pigeonhole principle.
B. Geometry (G)
Geometry problems are often considered the most challenging but are essential for a good score.
-
Focus: Properties of triangles (concurrency, orthocenter, circumcenter), circles (cyclic quadrilaterals, tangents), and basic coordinate geometry.
-
Tip: Mastering theorems like Ceva's and Menelaus's, and using techniques like angle chasing and similarity, are crucial.
C. Algebra (A)
Algebra is usually straightforward but requires careful manipulation.
-
Focus: Polynomials (roots and coefficients), functional equations, inequalities (AM-GM, Cauchy-Schwarz), and manipulation of quadratic equations.
-
Tip: Be proficient in manipulating expressions and constructing proofs for inequalities.
D. Combinatorics (C)
This section typically tests logical and systematic counting methods.
-
Focus: Basic counting principles (permutations and combinations), Pigeonhole Principle, and simple graph theory concepts.
-
Tip: Understanding the difference between counting arrangements and counting selections is vital. Problems often require constructing a one-to-one correspondence or proving an exhaustive count.