RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.2 Trigonometric Ratios

RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.2: Chapter 5, Exercise 5.2 in RD Sharma's Class 10 Maths book covers Trigonometric Ratios, focusing on understanding and calculating the ratios of angles in right-angled triangles. Trigonometric ratios—sine, cosine, tangent, cotangent, secant, and cosecant—are introduced based on the triangle’s side lengths (opposite, adjacent, and hypotenuse).

Checkout Class 10th Sample Papers from PW Store

RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.2 Overview

RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.2 PDF

RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.2 Trigonometric Ratios

Evaluate each of the following:

1. sin 45 ^∘ sin 30 ^∘ + cos 45 ^∘ cos 30 ^∘

Solution:

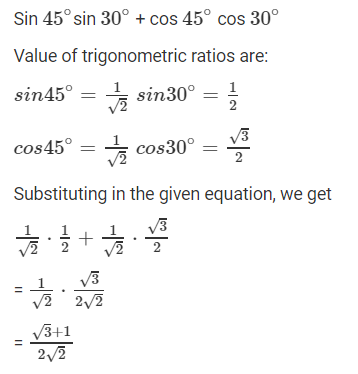
2. sin 60 ^∘ cos 30 ^∘ + cos 60 ^∘ sin 30 ^∘

Solution:

3.  cos 60 ^∘ cos 45 ^∘ – sin 60 ^∘ sin 45 ^∘

Solution:

4. sin ² 30 ^∘ + sin ² 45 ^∘ + sin ² 60 ^∘ + sin ² 90 ^∘

Solution:

5.  cos ² 30 ^∘ + cos ² 45 ^∘ + cos ² 60 ^∘ + cos ² 90 ^∘

Solution:

6. tan ² 30 ^∘ + tan ² 45 ^∘ + tan ² 60 ^∘

Solution:

7. 2sin ² 30 ^∘ − 3cos ² 45 ^∘ + tan ² 60 ^∘

Solution:

8. sin ² 30 ^∘ cos ² 45 ^∘ + 4tan ² 30 ^∘ + (1/2) sin ² 90 ^∘ − 2cos ² 90 ^∘ + (1/24) cos20 ^∘

Solution:

9. 4(sin ⁴ 60 ^∘ + cos ⁴ 30 ^∘ ) − 3(tan ² 60 ^∘ − tan ² 45 ^∘ ) + 5cos ² 45 ^∘

Solution:

10. (cosec ² 45 ^∘ sec ² 30 ^∘ )(sin ² 30 ^∘ + 4cot ² 45 ^∘ − sec ² 60 ^∘ )

Solution:

11.  cosec ³ 30 ^∘ cos60 ^∘ tan ³ 45 ^∘ sin ² 90 ^∘ sec ² 45 ^∘ cot30 ^∘

Solution:

12. cot ² 30 ^∘ − 2cos ² 60 ^∘ − (3/4)sec ² 45 ^∘ – 4sec ² 30 ^∘

Solution:

13. (cos0 ^∘ + sin45 ^∘ + sin30 ^∘ )(sin90 ^∘ − cos45 ^∘ + cos60 ^∘ )

Solution:

15. 4/cot ² 30 ^∘ + 1/sin ² 60 ^∘ − cos ² 45 ^∘

Solution:

16. 4(sin ⁴ 30 ^∘ + cos ² 60 ^∘ ) − 3(cos ² 45 ^∘ − sin ² 90 ^∘ ) − sin ² 60 ^∘

Solution:

17.

Solution:

18.

Solution:

19.

Solution:

Find the value of x in each of the following: (20-25)

20. 2sin 3x = √3

Solution:

Benefits of Solving RD Sharma Solutions Class 10 Maths Chapter 5 Exercise 5.2

Strengthens Conceptual Understanding : Trigonometric ratios are foundational concepts in trigonometry. Solving RD Sharma problems helps reinforce understanding of these ratios (sine, cosine, tangent, etc.) and how they relate to angles in right triangles.

Builds Problem-Solving Skills : RD Sharma exercises provide a variety of problems with different levels of difficulty, encouraging students to apply concepts in multiple ways. This enhances problem-solving abilities and analytical thinking.

Improves Accuracy and Speed : By practicing repeatedly, students become more accurate in their calculations and improve their speed in identifying which trigonometric ratios to use in different scenarios.

Exam-Oriented Practice : RD Sharma solutions are aligned with the CBSE syllabus, making them an excellent resource for exam preparation. Practicing these solutions familiarizes students with question patterns they might encounter in exams.

Boosts Confidence : Solving exercises successfully builds confidence, especially in a subject like trigonometry that students often find challenging. With regular practice, students become more comfortable tackling complex trigonometric problems.