Reflection Of Light
Light of Class 10
REFLECTION OF LIGHT
When a beam of light falls on any surface, a part of that is sent back into the same medium from which it is coming. This phenomenon is known at the reflection of light.
Reflection of light is of two types:

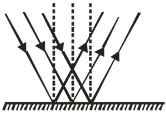
REGULAR REFLECTION
|
When the reflecting surface is smooth and well polished, e.g. mirror, the parallel rays falling on it are reflected parallel to one another i.e. the reflected light goes in one particular direction as shown in the figure. Then it is known as a regular reflection. The laws of reflection are valid only in regular reflection. It is the regular reflection that makes the object visible. |
Regular Reflection |
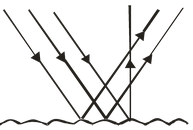
IRREGULAR REFLECTION:
|
When the reflecting surface is rough, the parallel rays falling on it are reflected in different directions as shown in the figure. Such a reflection is known as irregular reflection or diffused reflection or scattering of light. Laws of reflection are not valid in irregular reflection. In this case only the surface is visible and not the image. |
Irregular Reflection |
ANGLE OF REFLECTION:
The angle of reflection is the angle made by the reflected ray with the normal at the point of incidence.
Or
The angle between the reflected ray and normal to the surface is called the angle of reflection. In ∠BON is the angle of reflection.
SOME IMPORTANT TERMS ASSOCIATED WITH SPHERICAL LENSES
OPTICAL CENTRE:
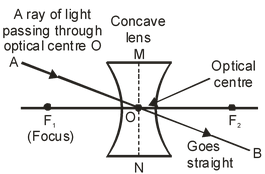
The centre point of a lens is known as its optical centre. It is usually represented by the letter O. A ray of light passing through the optical centre at a lens goes undeviated.
APERTURE:
The effective diameter of the circular outline at a spherical lens is called its aperture. In the figure (a), (b) ‘AB’ is the diameter of the circular outline of the lens which represents aperture of the lens or we can say that aperture is the actual refracting surface of the lens.
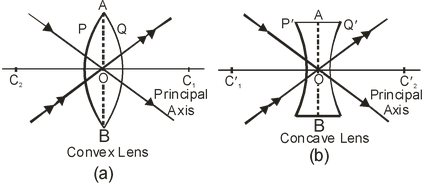
CENTRE OF CURVATURE:
A lens, either a convex lens or concave lens, has two spherical surfaces. Each of these surfaces form a part of a sphere. The centres of these spheres are called centres of curvature of the lens. The centre of curvature of a lens is usually represented by the letter C. Since there are two centres of curvature, we may represent them as C1 and C2.
PRINCIPAL AXIS:
An imaginary straight line passing through the two centres of curvature of a lens is called its principal axis.
PRINCIPAL FOCUS:
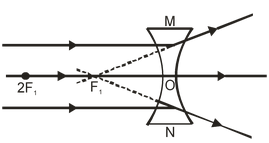
The principal focus of a concave lens is a point on its principal axis from which light rays parallel to the principal axis, appear to diverge after refraction by the lens. It is usually represented by the letter ‘F’. However a concave lens has two spherical surfaces and hence it has two principal foci or two focal points which are usually denoted by the letters ‘F1’ and ‘F2’ and are known as the first principal focus ‘F1’ and the second principal focus ‘F2’. The two foci of a lens are at equal distances from the optical centre, one an either side of the lens.
Since the light rays do not actually pass through the focus (or foci) of a concave lens, therefore, a concave lens has a virtual focus.
(i) First Principal Focus (F1) : The first principal focus (F1) of a concave lens is the virtual position of a point object on the principal axis of the lens, for which the image formed by the concave lens is at infinity. It is usually denoted by the letter ‘F1’, as shown in the figure (a)
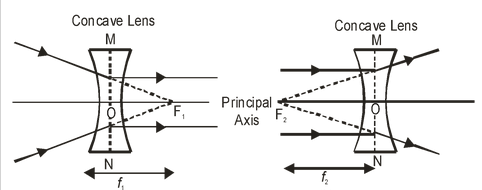
(ii) Second Principal Focus (F2): The second principal focus (F2) of a concave lens is the position of image point on the principal axis of the lens, when the object is situated at infinity. It is generally denoted by the letter (F2), as shown in the figure (b).
FOCAL LENGTH:
The distance of the principal focus (F1 or F2) from the optical centre ‘O’ of a lens is called its focal length. It is usually denoted by the letter ‘f ‘. Since a concave lens has two principal foci, so it has two focal lengths, known as : first focal length (f1) and second focal length (f2).
(i) First Focal Length (f1): The distance of first principal focus (F1) of the lens from optical centre ‘O’ of the lens is called first focal length of concave lens. It is represented by ‘F1’. i.e. OF1 = f 1. [see (a) in above figure].
(ii) Second Focal Length (F2): The distance of second principal focus (F2) of the lens from the optical centre ‘O’ of the lens is called second focal length of concave lens. It is represented by ‘f2’. i.e. OF2 = f2 [see (b) in above figure].
Rules for the formation of images by Convex Lens:
The positions of the image formed by a convex lens can be found by considering two of the following rays (as explained below).
(i) A ray of light coming parallel to principal axis, after refraction through the lens, passes through the principal focus (F) as shown in the figure.
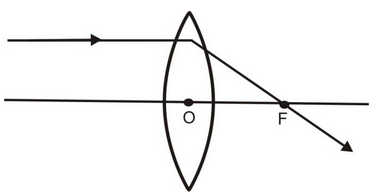
Convex Lens
(ii) A ray of light passing through the optical centre O of the lens goes straight without suffering any deviation as shown in the figure.
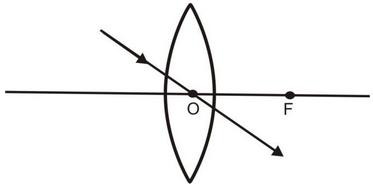
(iii) A ray of light coming from the object and passing through the principal focus of the lens after refraction through the lens, becomes parallel to the principal axis.
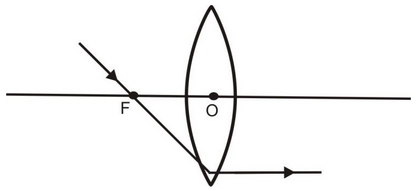
Image formed by Convex Lens:
The position, size and nature of the image formed by a convex lens depends upon the distance of the object from the optical centre of the lens. For a thin convex lens, the various case of image formation are explained below :
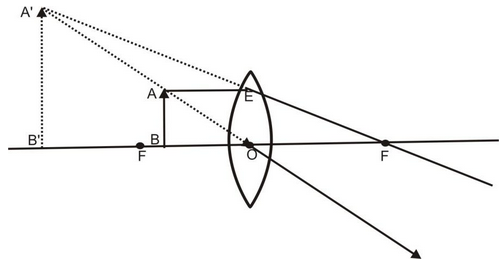
(i) When object at infinity:
When an object lies at infinity, the rays of light coming from the object may be regarded as a parallel beam of light. The ray of light BO passing through the optical centre O goes straight without any deviation. Another parallel ray AE coming from the object, after refraction, goes along EA’ Both the refracted rays meet at A’ in the focal plane of the lens. Hence, a real, inverted and highly diminished image is formed on the other side of the lens in its focal plane.
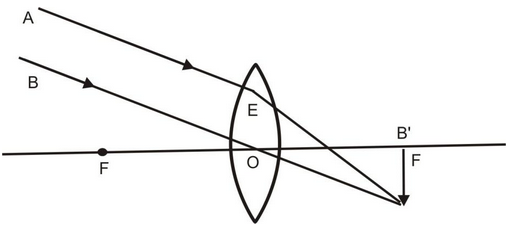
Real, Inverted and highly diminished image
(ii) When object lies beyond 2F:
When the object lies beyond 2F, its real, invert and diminished image is formed between F and 2F on the other side of the lens as explained below:
A ray of light AE coming parallel to the principal axis, after refraction, passes through the principal focus F and goes along EF. Another ray AO passing through the optical centre O goes straight without suffering any deviation. Both the refracted rays meet at A’. Hence, a real, inverted and diminished image is formed between F and 2F on the other side of the convex lens.
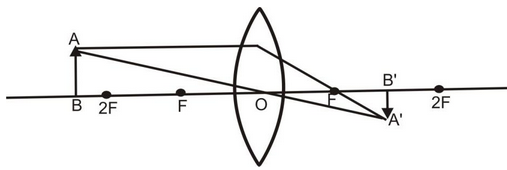
Real, inverted and diminished image
(iii) When object lies at 2F:
When an object lies at 2F, its real & inverted image having same size as that of the object is formed on the other side of the convex lens as explained below :
A ray of light AE coming parallel to the principal axis, after refraction, passes through the principal focus F and goes along EF. Another ray AO passing through the optical centre O goes straight without suffering any deviation. Both the refracted rays meet at A’. Hence a real, inverted image having the same size as the of the object is formed at 2F on the other side of the lens.
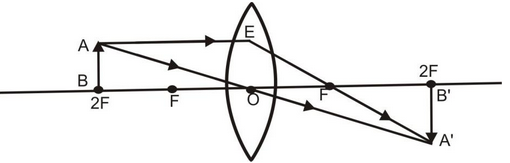
(iv) When object lies between F and 2F.
When an object lies between F and 2F in front of a convex lens, its real, inverted and magnified image is formed beyond 2F on the other side of the lens an explained below:
A ray of light AE coming parallel to the principal axis, after refraction, passes through the principal focus F and goes along EF. Another ray of light AO passing through the optical centre goes straight without any deviation. Both these refracted rays meet at A’. Hence a real, inverted and magnified image is formed beyond 2F on the other side of the lens.
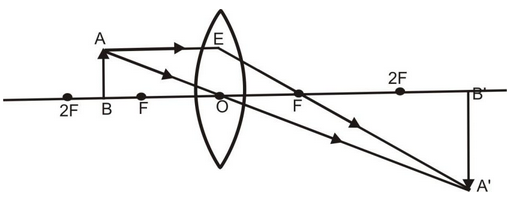
(v) When object lies at F:
When an object lies at the principal focus F of a convex lens, then its real, inverted and highly magnified image is formed at infinity on the other side of the lens as explained below:
A ray of light AE coming parallel to the principal axis, after refraction, passes through the principal focus F and goes along EF. Another ray of light AO passing through the optical centre O goes straight without any deviation. Both these refracted rays are parallel to each other and meet at infinity. Hence, a real, inverted, highly magnified image is formed at infinity on the other side of the lens.
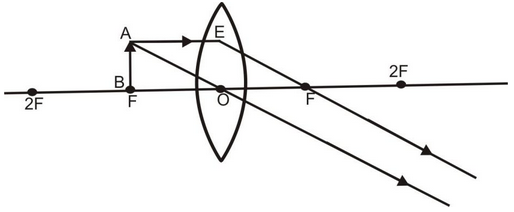
Meet at infinity
(vi) When object lies between O and F:
When an object lies between the optical centre O and the principal focus F of a convex lens, then its virtual, erect and magnified image is formed on the same side as that of the object as explained below :
A ray of light AE coming parallel to the principal axis, after refraction, passes through the principal focus F and goes along EF. Another ray of light AO passing through the optical centre goes straight without any deviation. Both these refracted rays appears to meet at A’. When produced backward. Hence a virtual, erect and enlarged image is obtained on the same side of the lens.
The results of image formation by a convex lens are summarised in the table:
|
Position of the object |
Positon of the image |
Size of the image |
Nature of the image |
|
At infinity |
At the focus F |
Highly diminished |
Real and inverted |
|
Beyond 2F |
Between F and 2F |
Diminished |
Real and inverted |
|
At 2F |
At 2F |
Same size |
Real and inverted |
|
Between F and 2F |
Beyond 2F |
Magnified |
Real and inverted |
|
At F |
At infinity |
Highly magnified |
Real and inverted |
|
Between O and F |
On the side of the object |
Magnified |
Virtual and erect |
HOW TO FIND OUT THE APPROXIMATE FOCAL LENGTH OF A CONVEX LENS:
To find out the approximate focal length of a convex lens, focus a distant object (at infinity) on a screen by using a convex lens whose focal length is to be determined. The sharp and inverted image of this object will be formed at the focus of the convex lens. The distance of the image so formed from the convex lens is equal to the focal length of convex lens. Measure this distance with the help of a scale. It will give us the approximate focal length of the convex lens.
RULES FOR TRACING IMAGES FORMED BY CONCAVE LENS:
When an object is placed in front of a concave lens, its image is formed at a point where at least two refracted light rays appear to meet. To trace the position and nature of the image formed by a concave lens, the three rays of light are commonly used, out of which, we take any two rays of light (starting from the object) whose paths, after refraction from the lens are known to us and are easy to draw. We may call them (the three rays) as rules for tracing images in concave lens. These are as follows:
(i) A ray of light which is parallel to the principal axis of a concave lens, appears to be coming from its focus after refraction through the lens, as shown in the figure below.
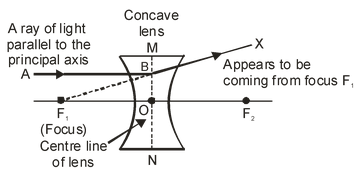
|
(ii) A ray of light passing through the optical centre ‘O’ of a concave lens goes straight (undeviated) after refraction through the lens, as shown in the figure. |
|
|
|
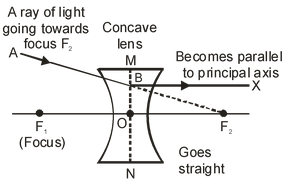
(iii) A ray of light appearing to pass towards the focus of a concave lens, becomes parallel to its principal axis after refraction through the lens, as shown in the figure. |
|
|
FORMATION OF DIFFERENT TYPES OF IMAGES BY A CONCAVE LENS IN DIFFERENT POSITION OF THE OBJECT:
The type of image formed by a concave lens primarily depends upon the position of the object in front of the lens. When the object is moved closer to the lens, starting from infinity, the following two cases arise.
|
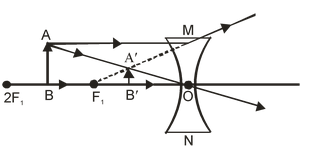
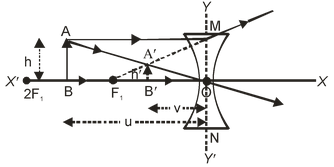
(i) When the object is at infinity: When the object is at infinity all the incident rays of light become parallel to the principal axis of the concave lens and appear to be coming from its focus after refraction through the lens. Hence the image formed is- (a) At focus F1 (on the same side of the lens as the object). (b) Virtual and erect. (c) Highly diminished, point sized. |
|
|
(ii) When the object is placed between infinity and optical centre ‘O’ of the concave lens: When the object is placed anywhere between the infinity and the optical centre ‘O’ of the concave lens, the image formed is- (a) Between focus (F1) and optical centre ‘O’ (on the same side of the lens as the object). (b) Virtual and erect. (c) Diminished (smaller than the object). |
|
Nature, position and size of the image formed by a concave lens for various positions of the object:
|
Position of the Object |
Position of the image |
Size of the image |
Name of the image |
|
At infinity |
At focus F1 |
Highly diminished, point-sized |
Virtual and erect |
|
Between infinity and optical centre O of the lens |
Between focus F1 and optical centre O |
Diminished |
Virtual and erect |
METHOD TO DISTINGUISH BETWEEN A CONVEX LENS AND A CONCAVE LENS WITHOUT TOUCHING THEM:
To distinguish between a convex lens and a concave lens without touching them keep the two lenses close to the page of a book and look for image of the writing on the page through the lens. If the writing (letters) of the book appears enlarged, the lens is convex, and if the writing (letters) appears diminished, then it is a concave lens.
This is because, when an object is within the focus of a convex lens, it produces an enlarged image, whereas a concave lens produces a diminished image for all positions of the object.
IN CASE OF A CONCAVE LENS:
A concave lens always form a virtual and erect image.
(i) For virtual and erect image: According to the new Cartesian sign convention, for the virtual and erect images formed by a concave lens,
Object height (h) is always +ve
Image height (h′) is always +ve
∴ Linear magnification, m = h'/h
or m = +ve/+ve
or m = +ve
|
|
In case of a concave lens, which always forms virtual and erect image, the magnification is always +ve. |
FOR SPHERICAL LENSES:
- If linear magnification, m > 1, then the image is enlarged i.e., bigger than the object.
- If linear magnification, m = 1, then the image is of the same size as the object.
- If linear magnification, m < 1 the image is diminished i.e., the image is smaller than the object.
- If the magnification ‘m’ is +ve the image is virtual and erect. And if the magnification ‘m’ is –ve the image will be real and inverted.
|
|
(i) A concave Lens always forms an image smaller than the object. Therefore linear magnification (m) of a concave lens is less than one. (ii) A convex lens forms an image (i) equal in size to the object (i.e. m = 1) (ii) less than the size of the object (i.e. m<1) (iii) more than the size of the object (i.e. m > 1). Therefore linear magnification of a convex lens can be one, less than one or more than one. |
SOME IMPORTANT CONCLUSIONS
On the basis of the New Cartesian Sign Convention discussed above, we can draw the following conclusions for the spherical lenses (convex as well as concave lenses).
IN CASE OF CONVEX LENS:
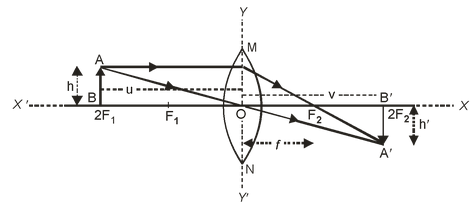
(i) For real and inverted image
Focal length (f ) = +ve
Object distance (u) = –ve
Object height (h) = +ve
Image distance (v) = +ve
Image height (h′) = –ve
Magnification (m) = –ve
|
|
In the case of a convex lens, for real and inverted image, the object distance and image height are – ve and remaining all distances are +ve. |
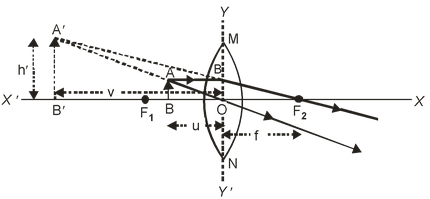
(ii) For virtual and erect image
Focal length (f ) = +ve
Object distance (u) = –ve
Object height (h) = +ve
Image distance (v) = –ve
Image height (h′) = +ve
Magnification (m) = +ve
|
|
In the case of a convex lens, for virtual and erect image, the object distance (u) and image distance (v) are –ve and remaining all distances are +ve. |
IN CASE OF CONCAVE LENS:
Since a concave lens always forms virtual and erect image therefore
For virtual and erect image
Focal length (f ) = –ve
Object distance (u) = –ve
Object height (h) = +ve
Image distance (v) = –ve
Image height (h′) = +ve
Magnification (m) = +ve
|
|
For a concave lens, object height (h) and image height (h′) are always +ve and remaining all distances are –ve. |