Special Types of Matrices

Special Types of Matrices

(i) Square Matrix

An m × n matrix for which m = n(i.e. the number of rows is equal to the number of columns) is called a square matrix of order n. The element aij of a square matrix
A = [aij]n × n for which i = j i.e., the elements a11, a22,…,ann are called the diagonal elements.

The matrix

A = 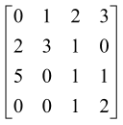is a square matrix of order 4.

The elements 0, 3, 1, 2 are the diagonal elements of A.

(ii) Null Matrix or Zero Matrix

The m × n matrix whose all elements are zero is called a null matrix of order
m × n. It is usually denoted by O.

(iii) Unit Matrix or Identity Matrix

A square matrix each of whose principal diagonal element is '1' and each of whose non−diagonal element is equal to zero is called a unit matrix or an identity matrix and is denoted by I. In will denote a unit matrix of order n

e.g. I3 = & I2 =

(iv) Scalar Matrix

A diagonal matrix whose diagonal elements are all equal is called a scalar matrix

e.g. A =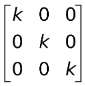

(v) Diagonal Matrix

A square matrix A = [aij]n × n is called a diagonal matrix if aij = 0 for all i ≠ j, i.e.,

A = 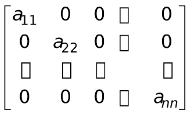(also represented as diag. (a11, a22, … , ann)).

(vi) Upper Triangular Matrix

A square matrix A = [aij]n×n is called an upper triangular matrix if aij = 0 whenever i > j i.e., e.g. A =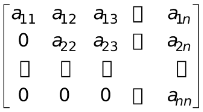

(vii) Lower Triangular Matrix

A square matrix A = [aij] is called a lower triangular matrix if aij = 0 whenever i < j i.e.,

A =

(viii) Row Matrix

Any 1 × n matrix which has only one row & n columns is called a row matrix.

e.g. X = 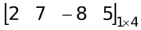is a row matrix.

(ix) Column Matrix

Any m × 1 matrix which has only one column & m rows is called a column matrix.

e.g. Y = is a column matrix.