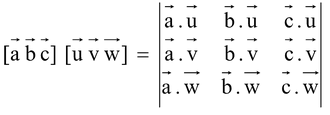Scalar Triple Product
Vector of Class 12
Scalar Triple Product
If  ,
,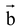 ,
,.png) are three vectors then(
are three vectors then( x
x 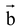 ).
)..png) is called the scalar triple product of these three vectors and is conventionally represented by [
is called the scalar triple product of these three vectors and is conventionally represented by [ 
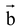
.png) ]. It is also known as box product. Geometrically it denotes the volume of a parallelepiped whose conterminous edges are represented by
]. It is also known as box product. Geometrically it denotes the volume of a parallelepiped whose conterminous edges are represented by 
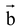
.png)
Properties of Scalar Triple Product
(a) 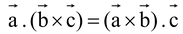
(b) 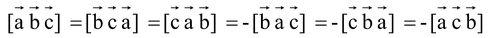
(c) If k is a scalar then; also 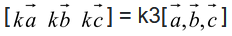
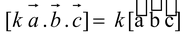
(d) If 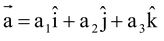
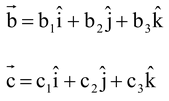
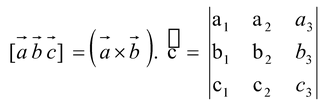
(e) The value of scalar triple product, if two of its vectors are equal is zero
i.e. 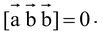 .
.
(f) Also 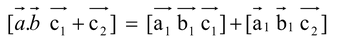
(g) The volume of a tetrahedron whose adjacent sides are represented by the vectors 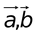 . and
. and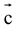 is
is 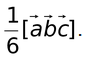 The position vectors of the centroid of a tetrahedron whose vertices are
The position vectors of the centroid of a tetrahedron whose vertices are  ,
,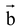 ,
,.png) and
and 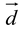 is
is 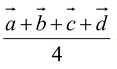 .
.
(h) The volume of a triangular prism whose adjacent sides are represented by 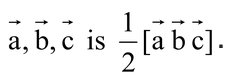 .
.
(i) If 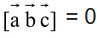 , then
, then  ,
,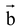 and
and .png) are coplanar
are coplanar
(j) Three vectors form a right handed or left handed system according as
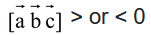
(k)