CO-ORDINATE SYSTEM
Coordinate Geometry of Class 9
Co-ordinate is the branch of Mathematics in which geometrical problems are solved through algebra by using a system known as co-ordinate system. In coordinate system, every point in a two dimensional plane can be represented by a unique ordered pair of real numbers.
ORDERED PAIR:
A pair of real numbers x and y listed in a specific order with ‘x’ at the first place and ‘y’ at the second place is called an ordered pair and written as (x, y). This ordered pair is also known as coordinates of a point in space.
(x, y) and (x, y) represent two different points. Both coordinate points are lying in different position.If x = y then both the points are representing the sameposition.
In two dimensional coordinate geometry, we use generally two types of co-ordinate system.
(i) Cartesian or Rectangular co-ordinate system.
(ii) Polar co-ordinate system.
In Cartesian co-ordinate system we represent any point by ordered pair (x,y) where x and y are called X and Y co-ordinate of that point respectively.
In polar co-ordinate system we represent any point by ordered pair (r,
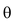 ) where ‘r’ is called radius vector and
) where ‘r’ is called radius vector and
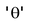 is called vectorial angle of that point. That we will study in higher class.
is called vectorial angle of that point. That we will study in higher class.
COORDINATE AXES:
X-COORDINATE :
The X-coordinate of a point is its perpendicular distance from Y-axis measured along the X-axis. The X-coordinate is also called the abscissa.
Y-COORDINATE :
The Y-coordinate of a point is its perpendicular distance from X-axis. The Y-coordinate is also called ordinate.
Draw two straight lines XOX′ and YOY′ intersecting at right angles at the point O. These lines are called coordinate axes or axes of reference.
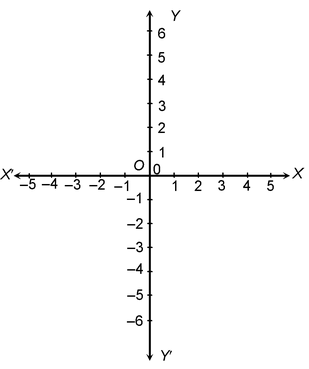
The horizontal line XOX′ is called x-axis.
The vertical line YOY′ is called y-axis.
The point O is called the origin.
OX represents positive x-axis.
OX′ represents negative x-axis.
OY represents positive y-axis.
OY′ represents negative y-axis.
Any convenient unit of length is selected and mark equal distances on both axes taking the origin as zero.
QUADRANTS:
The coordinate axes XOX′ and YOY′ divide the plane of paper into 4 regions. XOY, YOX′, X′OY′, Y′OX. These four regions are called the first, the second, the third and the fourth quadrant respectively.
The distance measured along x-axis is called x-coordinate or abscissa.
The distance measured along y-axis is called y-coordinate or ordinate.
While representing the coordinates of a point, x-coordinate should be written first and y. Coordinate should be written second. The P(x, y) represents the coordinates of a point P in a plane.
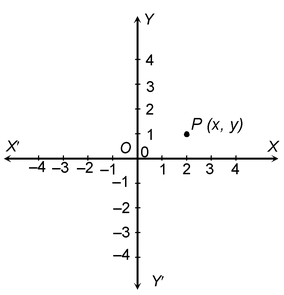
CONVENTION OF SIGNS:
As discussed earlier that regions XOY, X`OY, X`OY` and XOY` are known as the first, second, third and fourth quadrants respectively. The ray OX is taken as positive X-axis, OX` as negative X-axis, OY as positive Y-axis and OY` as negative Y-axis. Thus we have,
In first quadrant : X > 0, Y> 0 (Positive quadrant)
In second quadrant: X < 0, Y > 0
In third quadrant : X < 0, Y < 0 (Negative quadrant)
In fourth quadrant: X > 0, Y < 0
LEARN IT
(i)In quadrant I (+, +) both X-coordinate and Y-coordinate are positive.
(ii)In quadrant II (–, +) X-coordinate is negative where as Y-coordinate is positive.
(iii)In quadrant III (–, –) both X-coordinate and Y-coordinate are negative.
(iv)In quadrant IV (+, –) X-coordinate is positive where as Y-coordinate is negative.
(v)The coordinates of origin are (0, 0) i.e. X-coordinate is zero as well as
Y-coordinate is also zero.
POINTS ON AXIS:
In point P lies on X-axis then clearly its distance from X-axis will be zero, therefore we can say that its coordinate will be zero. In general, if any point lies on X-axis then its y-coordinate will be zero. Similarly if any point Q lies on Y-axis, then its distance from Y-axis will be zero therefore we can say its x-coordinate will be zero. In general, if any point lies on Y-axis then its x-coordinate will be zero.
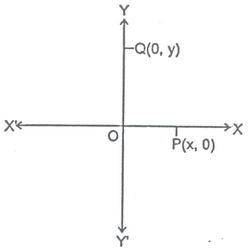
PLOTTING OF POINTS:
In order to plot the points in a plane, we may use the following algorithm.
Step I: Draw two mutually perpendicular lines on the graph paper, one horizontal and other vertical.
Step II: Mark their intersection point as O (origin).
Step III: Choose a suitable scale on X-axis and Y-axis and mark the points on both the axis.
Step IV: Obtain the coordinates of the point which is to be plotted. Let the point be P(a,b). To plot this point start from the origin and |a| units move along OX, OX’ according as ‘a’ is positive or negative respectively. Suppose we arrive at point M. From point M move vertically upward or downward |b| through units according as ‘b’ is positive or negative. The point where we arrive finally is the required point P(a,b).
1. Plot the point (3,4) on a graph paper.
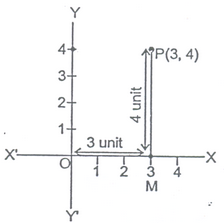
Solution: Let X`IX and Y`OY be the coordinate axis. Here given point is P(3,4), first we move 3 units along OX as 3 is positive then we arrive a point M. Now from M we move vertically upward as 4 is positive. Then we arrive at P(3,4).
2. Write the quadrants for the following points.
(i) A(3, 4) (ii) B(-2, 3) (iii) C(-5, -2) (iv) D(4, -3)
(v) E(-5, -5)
Solution: (i) Here both coordinates are positive therefore point A lies in Ist quadrant.
(ii) Here x is negative and y is positive therefore point B lies in IInd quadrant.
(iii) Here both coordinates are negative therefore point C lines in IIIrd quadrant.
(iv) Here x is positive and y is negative therefore point D lies in IVth quadrant.
(v) Point E lies in III quadrant.
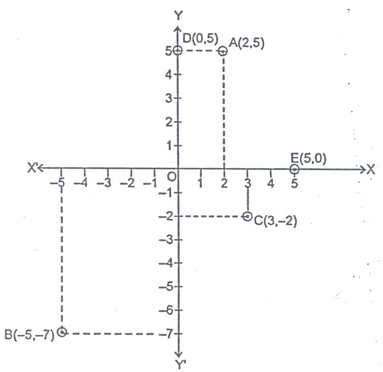
3. Plot the following points on the graph paper.
(i) A(2 ,5) (ii) B(-5,-7) (iii) C(3,-2) (iv) D (0,5)
(v) E(5,0)
Solution: Let XOX` and YOY`be the coordinate axis. Then the given points may be plotted as given below: