Gravitation is the phenomenon of attraction between any two bodies of the universe. Gravity is one particular case of gravitation when one of the two attracting bodies is Earth. Hence, gravity is the phenomenon of attraction between Earth and any other body. The force of attraction exerted by Earth on the body is called force of gravity.
The force of gravity is calculated using Universal Law of Gravitation given by Newton as,
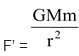
Where m = mass of the body
M = mass of earth
r = distance of the body from the centre of Earth
F = force of gravity exerted by Earth on the body
ACCELERATION DUE TO GRAVITY:
When a body is dropped from a certain height, it falls with a constant acceleration.
This uniform acceleration produced in a freely falling body due to the gravitational pull of the earth is known as acceleration due to gravity and it is denoted by the letter ‘g’.
Although g varies very slightly from place to place but its average value is taken to be 9.8 m/s
2
.
This means that the velocity of a body increases by 9.8 m/s every second. Say, if the body is dropped with zero velocity, its velocity becomes 9.8 m/s after 1s; 19.6 m/s after 2s; 27.4 m/s after 3s and so on. Similarly, if a body is projected upwards, its velocity decreases by 9.8 m/s after every second.
Gravitation and Gravity
Gravitation is the force of attraction between any two bodies whereas gravity is the force of attraction between two bodies when one of the two bodies is earth. Hence gravity is a special case of gravitation.
RELATION BETWEEN ‘g’ AND ‘G’:
The differences between G and g should be clearly understood. They have different values and different units. G is a universal constant whereas g has to be defined separately for the earth, the moon, the sun, Mars, etc. In each case g will have a different value. Also, if one goes above the earth’s surface goes into a deep mine, the value of g changes.
DIFFERENCE BETWEEN ‘g’ AND ‘G’:
|
Acceleration due to gravity (g)
|
Universal gravitational constant (G)
|
|
1. The acceleration produced in a body falling freely under the action of gravitational pull of the earth is known as acceleration due togravity.
|
1. The gravitational force between two bodies of unit masses separated by a unit distance is known as universal gravitational constant.
|
|
2. The value of ‘g’ is different at different points on the earth.
|
2. The value of ‘G’ is same at every point on the earth.
|
|
3. The value of ‘g’ decreases as we go higher from the surface of the earth or as we go deep into the earth.
|
3. The value of ‘G’ does not change with height and depth from the surface of the earth.
|
|
4. The value of ‘g’ at the centre of the earth is zero.
|
4. The value of ‘G’ is not zero at the centre of the earth or anywhere else.
|
|
5. The value of ‘g’ is different on the surface of different heavenly bodies like the sun, moon, and the planets.
|
5. The value of ‘G’ is same throughout the universe.
|
|
6. The value of ‘g’ on the surface of the earth is 9.8 ms
-2
.
|
6. The value of G = 6.673 × 10
-11
Nm
2
kg
-2
throughout the universe.
|
Case I:
If we drop a body (say, a stone) of mass ‘m’ from a distance ‘d’ from the center of the earth of mass M, then the force exerted by the earth on the stone is given by Newton’s law of gravitation as:
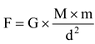… (i)
We also know from the second law of motion that force is the product of mass and acceleration. We already know that there is acceleration involved in falling objects due to the gravitational force and is denoted by g.
Therefore, the magnitude of the gravitational force F will be equal to the product of mass and acceleration due to the gravitational force, that is,
F = m x g …(ii)
From equation (i) and (ii)
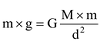
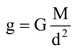
Case-II:
Let an object be on or near the surface of the earth. The distance d will be equal to R, the radius of the earth. Thus, for objects on or near the surface of the earth,
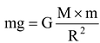
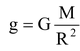
The earth is not a perfect sphere. As the radius of the earth increases from the poles to the equator, the value of ‘g’ becomes greater at the poles than at the equator.
VALUE OF g ON EARTH:
To calculator the value of g, we should put the values of G = 6.7 x 10
-11
Nm
2
/kg
2
; mass of the earth M = 6 x 10
24
kg and radius of the earth (R) = 6.4 x 10
6
m, in the formula :
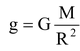
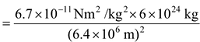
= 9.8 m/s
2
Thus, value of acceleration due to gravity of the earth, g = 9.8 m/s
2
VALUE OF g ON MOON:
Mass of moon
= 7.4 x 10
22
kg
Radius of moon
= 1,740 km
= 1,740,000 m = 1.74 x 10
6
m
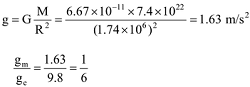
ACCELERATION DUE TO GRAVITY (g) DOES NOT DEPEND UPON MASS OF THE BODY:
The relation between g and G is
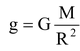
Where, G = gravitational constant,
M = mass of Earth, and
R = radius of Earth.
We observe from this relation that value of g depends on mass of Earth and radius of Earth. Mass of the body (m) is nowhere involved in this relation. It means that the value of acceleration due to gravity does not depend upon mass of the body. Hence, all bodies when free will falls towards the centre of earth with the same acceleration – whatever be their masses. It means that a big stone and a small stone when dropped from a particular height will move with the same acceleration due to gravity. Both will strike the ground at the same time whenever they fall under gravitational pull alone (vacuum).
VARIATION IN ACCELERATION DUE TO GRAVITY (g):
The relation between g and G is
|
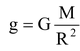
It shows that value of g depends on gravitational constant G, mass of Earth M and radius of the Earth R. Now, G and M both are constants. But radius of earth R is not constant as Earth is not a perfect sphere. Therefore, value of g changes from place to place on the surface of earth. These changes are briefly discussed here.
|
|
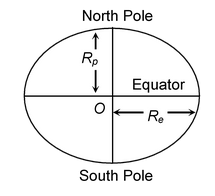
(a) Effect of shape of Earth on 'g'
As is known, Earth is flattened at the poles and bulged out at the equator. Therefore, polar radius of Earth = R
p
is minimum, and equatorial radius of Earth = R
p
is maximum.
Acceleration due to gravity at poles,
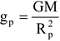= maximum, as R
p
is minimum
Acceleration due to gravity at equator,
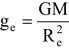= minimum, as R
e
is maximum
(b) Effect of height above the surface of Earth on 'g'
As we move above the surface of the Earth, the distance (r) from the centre of earth increases. As
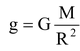, therefore, value of acceleration due to gravity decreases with height above the surface of Earth.
(c) Effect of depth below the surface of Earth on 'g'
Most of you might be thinking that as we go down the surface of Earth, the value of radius of Earth R decreases. Therefore, g must be increasing. But it is not true. You will learn in higher classes that the value of acceleration due to gravity decreases as we go down inside the Earth. So much so that at the centre of Earth, g = 0.
Hence, we conclude that value of acceleration due to gravity is maximum at the surface of Earth. It decreases as we move above the surface of Earth or go inside the surface of Earth.
Important Facts of ‘g’
-
From the expression
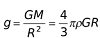it is clear that its value depends upon the mass radius and density of planet and it is independent of mass, shape and density of the body placed on the surface of the planet. i.e. a given planet (reference body) produces same acceleration in a light as well as heavy body.
-
The greater the value of (M/R
2
) or ρR greater will be value of g for that planet.
-
Acceleration due to gravity is a vector quantity and its direction is always towards the centre of the planet.
-
Dimension [g] = [LT
–2
]
-
it’s average value is taken to be 9.8 m/s
2
or 981 cm/sec
2
or 32 feet/sec
2
, on the surface of the earth at mean sea level.
-
The value of acceleration due to gravity vary due to the following factors : (a) Shape of the earth, (b) Height above the earth surface, (c) Depth below the earth surface and (d) Axial rotation of the earth.
EQUATIONS OF MOTION FOR FREELY FALLING OBJECT:
Equation of Motion of Freely Falling Bodies
When the bodies are falling under influence of gravity, they experience acceleration g i.e., 9.8 ms
–2
. However, when these are going up against gravity, they move with retardation of 9.8 ms
–2
. All the equations of motion already read by us are valid for freely falling body with the difference that a is replaced by g. For motions vertically upwards a is replaced by – g.
Thus equation of motion
General equationsof motion forof motionfreely falling bodies
-
v = u + at changes to v = u + gt
-
s = ut +1/2at
2
changes to h = ut + 1/2gt
2
-
v
2
= u
2
+ 2as changes to v
2
= u
2
+ 2gh
We shall use these modified equations to solve numerical problems. Before we do that, we should remember the following important points for the motion of freely falling bodies.
-
When a body is dropped freely from a height, its initial velocity ‘u’ becomes zero.
-
When a body is thrown vertically upwards, its final velocity ‘v’ becomes zero.
-
The time taken by a body to rise to the highest point is equal to the time it takes to fall from the same height.
-
The distance traveled by a freely falling body is directly proportional to the square of time of fall.
Sign Conventions:
-
g is taken as positive when it is acting in the same direction as that of motion and g is taken as negativewhen it is opposing the motion.
-
Distance measured upward from the point of projection is taken as positive, while distance measured downward from the point of projection is taken as negative.
-
Velocity measured away from the surface of earth (i.e. in upward direction) is taken as positive, while velocity measured towards the surface of the earth is taken as negative.
General equationsof motion forof motionfreely falling bodies
-
v = u + at changes to v = u + gt
-
s = ut +1/2at
2
changes to h = ut + 1/2gt
2
-
v
2
= u
2
+ 2as changes to v
2
= u
2
+ 2gh
We shall use these modified equations to solve numerical problems. Before we do that, we should remember the following important points for the motion of freely falling bodies.
-
When a body is dropped freely from a height, its initial velocity ‘u’ becomes zero.
-
When a body is thrown vertically upwards, its final velocity ‘v’ becomes zero.
-
The time taken by a body to rise to the highest point is equal to the time it takes to fall from the same height.
-
The distance traveled by a freely falling body is directly proportional to the square of time of fall.
Sign Conventions:
-
g is taken as positive when it is acting in the same direction as that of motion and g is taken as negativewhen it is opposing the motion.
-
Distance measured upward from the point of projection is taken as positive, while distance measured downward from the point of projection is taken as negative.
-
Velocity measured away from the surface of earth (i.e. in upward direction) is taken as positive, while velocity measured towards the surface of the earth is taken as negative.
