Keplers Laws
Gravitation of Class 11
Keplers Laws
First Law
The planets move around the sun in elliptical orbits with the sun at one focus.
An ellipse with two foci F 1 and F 2 is shown in the figure.
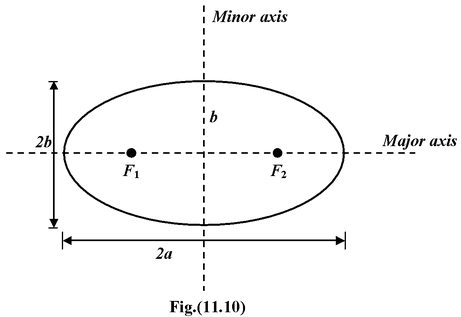
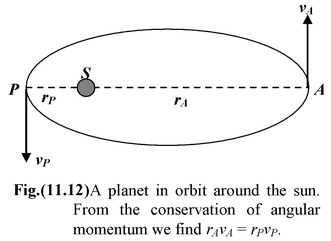
A circle is a special case in which the foci coincide at the center. The short dimension is called the minor axis and has length 2b; the long dimension is called the major axis and has length 2a. The closest point P, in the orbit to the sun is called the perihelion; the farthest point A, is called the aphelion.
Second Law
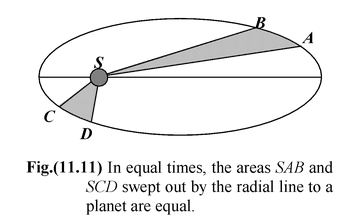
The line joining the sun to a planet sweeps out equal areas in equal time.
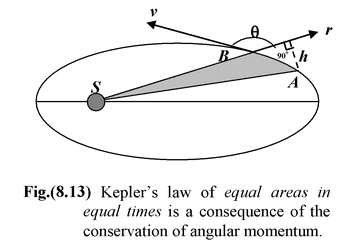
Suppose that in a given time interval a planet moves from A to B as shown in the figure, and from C to D during another time interval. According to the second law the areas SAB and SCD are equal. The speed of the planet, therefore, must vary during its orbit. It is greatest at the perihelion, and least at the aphelion. In example (11.5), this law is shown to be a consequence of the conservation of angular momentum.
|
|
|
Third Law
The square of the period of planet is proportional to the cube of its mean distance from the sun.
The mean distance turns out to be the semi-major axis, a.
Mathematically, T 2 ∝ a 3
orT 2 = κa 3
where κ is a constant that applies to all planets.
Example 11.5
According to Kepler's second law of planetary motion, the line joining the sun to a planet sweeps out equal areas in equal time intervals. Show that this is a consequence of the conservation of angular momentum. The path of the planet is an ellipse.
Solution
|
The gravitational force exerted by the sun on a planet is a central force − it acts along the line joining the two bodies, as shown in Fig(11.13). The torque on the planet is
which means that its angular momentum is constant. The constancy in direction implies that the plane of the orbit does not change. The constancy in magnitude leads to the "law of areas." In a time interval Δt, the planet moves from A to B by a distance AB = vΔt. The height of the triangle SAB is |
|
h = AB sin(180 − θ)° = vΔt sinθ
Thus, its area is
ΔA = 1/2rh = 1/2rvΔt sinθ
so,
ΔA/Δt = 1/2rv sinθ(i)
The angular momentum of the planet is
l = rp sinθ = mrp sinθ(ii)
Combining (i) and (ii) we see that
ΔA/Δt = L/2m = constant
The rate at which the radial line sweeps out area is constant. Or, equivalently, the radial line sweeps out equal areas in equal time intervals.
Example 11.6
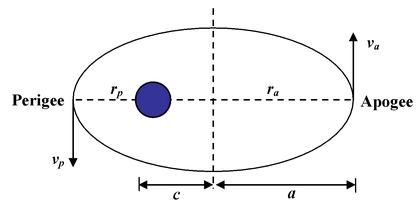
A planet moves around sun in an elliptical orbit of semi-major axis a and eccentricity e. If the mass of sun is M, find the velocity at the perigee and apogee.
|
Solution Let m be the mass of the planet. As it is clear from the figure, rP = a – c ra = a + c Applying the conservation of angular momentum at the perigee and apogee, we get mvprp = mvara
or
|
|
Using conservation of mechanical energy, we get
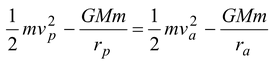
On rearranging, we get
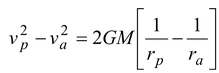 (ii)
(ii)
Substituting the value of vp = va
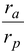 , we get
, we get
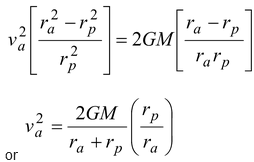
Since rp = a – c and ra = a + c, therefore,
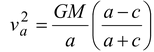
Since e = c/a , then va =
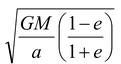
Putting the value in (i), we get
vp =
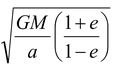
Example 11.7
|
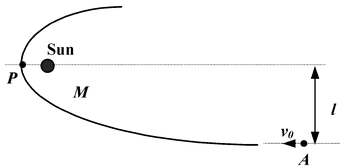
A cosmic body A coming from infinity with a velocity v0 is approaching the Sun of mass M, with its line of motion at a distance l from the Sun, as shown in the figure. When it gets closest to the Sun i.e. at P, what will be its distance from the
|
|
Solution
Applying energy conservation principle at infinity and at P.
Initial (gravitational PE + KE) = final ((gravitational PE + KE)
0 +
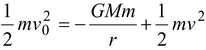 (i)
(i)
where M = mass of the sun
m = mass of the body
and r = distance of closest approach.
v = velocity at P
Since the angular momentum of the body about the sun will remain conserved, therefore,
(mv 0 )l = (mv)r
v 0 l = vr(ii)
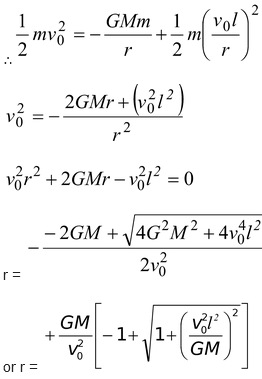
Note: Only +sign is taken for the closest approach. Negative sign is irrelevant.
Example 11.8
An artificial satellite of the earth (radius R and mass M) moves in an orbit whose radius is n times the radius of the earth. Assuming resistance to the motion to be proportional to the square of velocity that is F = av2. Find how long the satellite will take to fall on to the earth.
Solution
Energy of satellite E =
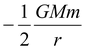
dE =
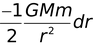
We have
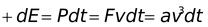
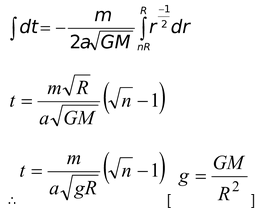
Example 11.9
.A planet moves along an elliptical orbit around the sun. At the moment when its distance from the sun is ro, its velocity is vo at an angle α to ro. Find the maximum and minimum distance of this planet from the sun. Mass of the sun = M.
Solution
From law of conservation of angular momentum
mvoro sin α = mvr
⇒vr = voro sin α
Conservation of energy demands
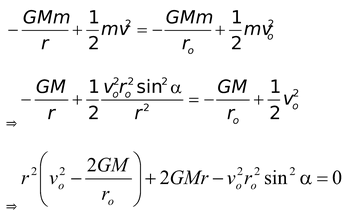
Again we have
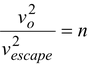 (pure number)
(pure number)
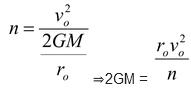 (2)
(2)
From (1) and (2),
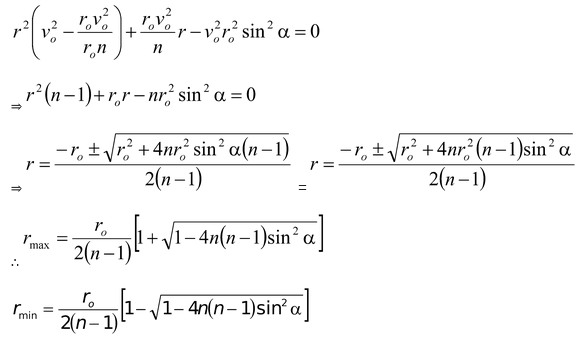
|
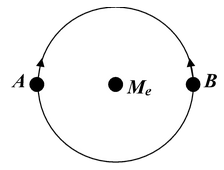
Example 11.10 Consider two satellite A and B of equal mass moving in the same circular orbit of radius r around the earth but in the opposite sense and therefore, on a collision course as shown in the figure. |
|
(a)Find the total mechanical energy EA + EB of the two satellite plus-earth system before collision.
(b)If the collision is completely inelastic find the total mechanical energy immediately after collision. Describe the subsequent motion of the combined satellite.
Solution
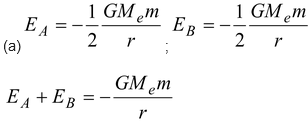
(b)According to conservation of momentum along the tangent
mv + (−mv) = 2mv′ ⇒ v′ = 0
Energy of the system = Gravitational energy
E =
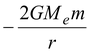
Since velocity = 0, system will fall vertically down.
Example 11.11
A double star is a system of two stars moving around the centre of mass of the system due to gravitation. Find the distance between the components of the double star if the total mass equals M and time period is T.
Solution
Let d = distance between stars
d1 and d2 are the distances of stars from c.m.
Therefore,
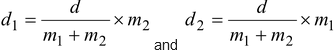
We have,
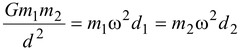
m 1 + m 2 = M (Given)
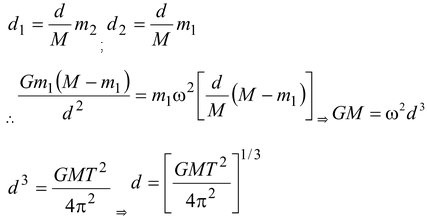

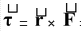 = rF sin 180°
= rF sin 180°
 = 0
= 0
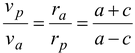 (i)
(i)