Parallelogram theorem

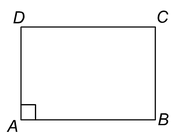
PARALLELOGRAM

A parallelogram is a quadrilateral in which both the pairs of opposite sides are parallel.

THEOREM 1:

A diagonal of a parallelogram divides it into two congruent triangles.

Given :AC is a diagonal of the parallelogram ABCD as shown in figure.

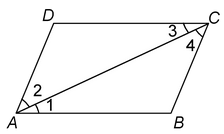
To prove:ΔABC≅ΔCDA.

Proof: We have AB || CD [Opposite sides of parallelogram ABCD]

⇒ ∠1 = ∠3 …(i) [Alternate angles with transversal AC]

Now, BC || AD [Opposite sides of parallelogram ABCD]

⇒ ∠2 = ∠4 …(ii) [Alternate angles with transversal AC]

In ΔABC and ΔCDA, we have

∠1 = ∠3 [From (i)]

∠2 = ∠4 [From (ii)]

and AC = CA [Common]

∴ ΔABC≅ ΔCDA [By ASA Congruence]

Hence Proved.

THEOREM 2:

In a parallelogram, opposite sides are equal.

Given: A parallelogram ABCD in which AB║DC and AD║BC.

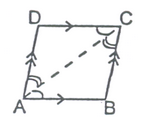
To Prove: Opposite sides are equal i.e., AB = DC and AD = BC

Construction: Join A and C

Proof: In ΔABC and ΔCDA

∠BAC = ∠DCA [Alternate angles]

∠BCA = ∠DAC [Alternate angles]

AC = AC [Common]

∴ ΔABC≅ΔCDA [By ASA]

⇒ AB = DC and AD = BC [By cpctc] Hence Proved.

THEOREM 3:

If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram 

Given: A quadrilateral ABCD in which

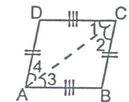
To Prove: ABCD is a parallelogram i.e., AB ║ DC and AD ║ BC

Construction: Join A and C

Proof: In ΔABC and ΔCDA

AB = DC [Given]

AD = BC [Given]

And AC = AC [Common]

∴ ΔABC≅ΔCDA [By SSS]

⇒ ∠1 = ∠3 [By cpctc]

And ∠2 =∠4 [By cpctc]

But these are alternate angles and whenever alternate angles are equal, the lines are parallel.

∴ AB ║ DC and AD ║ BC

⇒ ABCD is a parallelogram. Hence Proved.

Things to remember :

In order to prove that given quadrilateral is parallelogram, we have to prove that :

(i) Opposite angles of the quadrilateral are equal, or

(ii) Diagonals of the quadrilateral bisect each other, or

(iii) A pair of opposite sides is parallel and is of equal length, or

(iv) Opposite sides are equal.

(v) Every diagonal divides the parallelogram into two congruent triangles.

question Show that each angle of a rectangle is right angle.

But, ∠A = 90°

So, ∠B = 180°−∠A = 180°− 90° = 90°

Now, ∠C = ∠A and ∠D = ∠B [Opposite angles of the parallelogram]

So, ∠C = 90° and ∠D = 90°.

Therefore, each of the angles of a rectangle is a right angle.

Proof: Since, PQ ║ BC i.e., PR ║ BC [Given] and CR ║ BA i.e., CR ║ BP [By construction]

∴ Opposite sides of quadrilateral PBCR are parallel.

⇒ PBCR is a parallelogram

⇒ BP = CR

Also,BP = AP [As, P is mid-point of AB]

∴ CR = AP

∴ AB ║ CR and AC is transversal, ∠PAQ = ∠RCQ [Alternate angles]

∴ AB ║ CR and PR is transversal, ∠APQ = ∠CRQ [Alternate angles]

In ΔAPQ and ΔCRQ

CR = AP, ∠PAQ = ∠RCQ and ∠APQ = ∠CRQ

⇒ ΔAPQ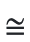ΔCRQ [By ASA]

⇒ AAQ = QC Hence Proved.

question ABCD is a trapezium in which AB ║ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (as shown). Prove that F is the mid-point of BC.

Solution: Given line EF is parallel to AB and AB ║ DC

∴ EF ║ AB ║ DC.

According to the converse of the mid-point theorem, is ΔABD, E is the mid-point of AD.

EP is parallel to AB [As EF ║ AB]

∴ P is mid-point of side BD

[The line through the mid-point of a side of a triangle and parallel to the other side, bisects the third side]

Now, in ΔBCD, P is mid-point of BD [Proved above]

And,PF is parallel to DC [As EF ║ DC]

∴ F is mid-point of BC

[The line through the mid-point of a side of a triangle and parallel to the other side, bisects the third side] Hence Proved

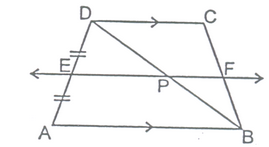
Remark:

In quadrilateral ABCD, if side AD is parallel to side BC; ABCD is a trapezium.

Now, P and Q are the mid-points of the non-parallel sides of the trapezium; then PQ=1/2 (AD + BC). i.e. The length of the line segment joining the mid-points of the two non-parallel sides of a trapezium is always equal to half of the sum of the lengths of its two parallel sides.

THEOREM5:

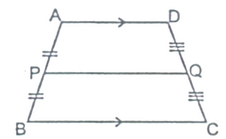
If there are three or more parallel lines and the intercepts made by them on a transversal are equal, then the corresponding intercepts on any other transversal are also equal. 

Given: Three parallel lines I, m and n i.e., I ║ m ║ n. A transversal p meets these parallel lines are points A, B and C respectively such that AB = BC. Another transversal q also meets parallel lines I, m and n at points D, E and F respectively.

To Prove: DE = EF

Construction: Through point A, draw a line parallel to DEF; which meets BE at point P and CF and point Q.

Proof: In ΔACQ, B is mid-point of AC and BP is parallel to CQ and we know that the line through the mid-point of one side of the triangle and parallel to another sides bisects the third side.

∴ AP = PQ ...(i)

When the opposite sides of a quadrilateral are parallel, it is a parallelogram and so its opposite sides are equal.

∴ AP ║ DE and AD ║ PE ⇒ APED is a parallelogram.

⇒ AP = DE ....(ii)

AndPQ ║ EF and PE ║ QF ⇒ PQFE is a parallelogram

⇒ PQ = EF ....(iii)

From above equations, we get

DE = EF Hence Proved.

question In the given figure, E and F are respectively, the mid-points of non-parallel sides of a trapezium ABCD.

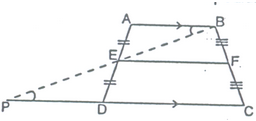
Prove that

(i) EF ║ AB