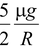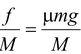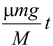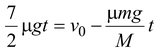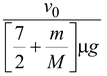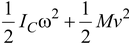Rolling Motion
Rotational Motion of Class 11
In a pure rolling motion a wheel rotates about its center of mass and the center of mass moves linearly so that it covers a distance equal to its circumference in one complete rotation. °
That is, s = 2πR
|
If T be the time period of one revolution, then dividing both the sides by T, we get
orvc = ωR (10.28) where ω is the angular velocity of the wheel about its center of mass, and vc is the linear velocity of the center of mass. |
|
Since rolling is a combination of translation of the center and rotation about the center, therefore, velocity of any point on the rim is the vector sum
v =v c + v' (10.29)
where v c is the velocity of the center of mass, and v′ is the velocity of the particle with respect to center of mass.
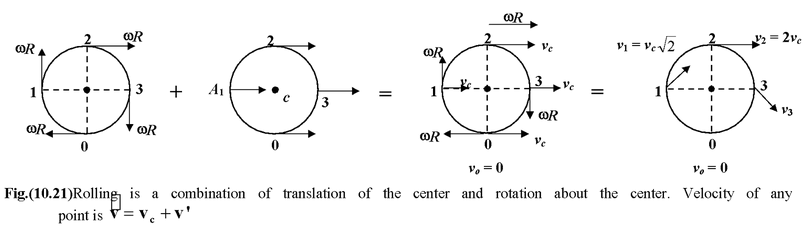
It is obvious from the figure (10.21), at the top point 2 of the wheel these two velocities are in the same direction, so v 2 = 2vc = 2ωR and at the bottom point O, they are in the opposite directions, so vo = 0.
|
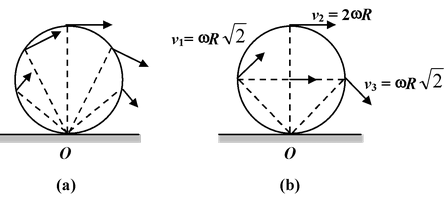
Since the wheel does not slip, the point of contact with the surface is instantaneously at rest and the wheel momentarily rotates about this point. The particle appear to describe circular paths with angular velocity ω about O as the center. The magnitude of the velocity of any point is given by the product of angular velocity ω with the distance of that point from the point of contact. |
Fig.(10.22)(a) When a wheel rolls without slipping the point of contact is instantaneously at rest and acts as the center of rotation. (b) Velocity of points 1, 2 and 3. |
The direction of the velocity vector is perpendicular to the line joining the point and the point of contact. The velocities of the point 1, 2 and 3 are shown in figure (10.22 b).
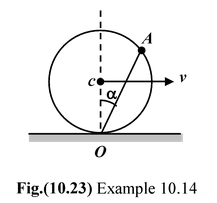
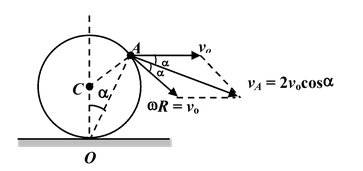
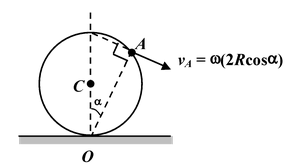
Example 10.14
|
A hoop of radius R rolls over a horizontal plane with a constant velocity vo without slipping. Find the velocity of point A of the loop as shown in figure. |
|
Solution
The velocity of the point A can be obtained in two ways:
|
Method I
|
Method II
|
Kinetic Energy of a Rolling Body
Since the rolling motion is a combination of linear velocity of the center and rotational motion about the center. Therefore, the total kinetic energy of a rolling body is given by
K =
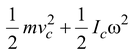 (10.30)
(10.30)
where
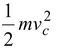 is the translational kinetic energy and
is the translational kinetic energy and
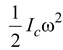 is the rotational kinetic energy about the center of mass
is the rotational kinetic energy about the center of mass
In pure rolling motion, vc = ωR
∴K =
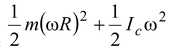
orK = 1/2 (Ic + mR2) ω 2
Using parallel axes theorem, the term Ic + mR 2 gives the moment of inertia about the point of contact, therefore,
Io = Ic + mR 2
and K = 1/2 I o ω 2 (10.31)
Note that equation (10.31) gives the rotational kinetic energy of the wheel about the point of contact.
Example 10.15
A hoop of mass m and radius R rolls without slippage with velocity vo. Find its kinetic energy.
Solution
|
Method I
K =
K =
since vo = ωR
∴K =
or K =
|
Method II K = 1/2I o ω 2 here I o = Ic + mR 2 or Io = mR 2 + mR 2 = 2mR 2 ∴ K = 1/2(2mR 2 ) ω 2
K = mR2ω
2
=
|
Application of Newton's Second Law in Rolling Motion
1.Write
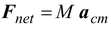 for the object as if it were a point−mass, that is, ignoring rotation.
for the object as if it were a point−mass, that is, ignoring rotation.
2.Write
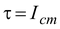 α as if the object were only rotating about the centre of mass, that is ignoring translation.
α as if the object were only rotating about the centre of mass, that is ignoring translation.
3.Use of no−slip condition
4.Solve the resulting equations simultaneously for any unknown.
Caution:
- In general, it is not the case that f = µN
- Be certain that the sign convention for forces and torques are consistent.
Example 10.16
|
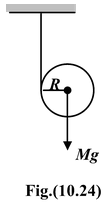
A solid cylinder of mass M has a string wrapped several times around its circumference. The free end of string is attached to the ceiling and the cylinder is released from rest. Find the acceleration of the cylinder and the tension in the string. |
|
Solution
|
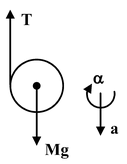
The free body diagram of the cylinder is shown in the figure. Applying Newton's second law Translation:Mg − T = Ma ..(i) Rotationτc = TR Sinceτc = Iα = (1/2 MR 2 )α ∴TR = (1/2 MR 2 )α |
|
or T = (MR/2)α..(ii)
Condition of no slipping, a = αr..(iii)
Solving equation (i), (ii) and (iii) we obtain
a = 2/3g
andT = Mg/3
Example 10.17
Figure shows a sphere of mass M and radius R that rolls without slipping down an incline. Its moment of inertia about a central axis is
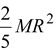 .
.
(a)Find the linear acceleration of the center of mass.
(b)What is the minimum coefficient of friction required for the sphere to roll without slipping?
Solution
|
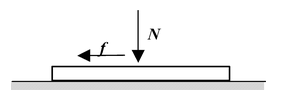
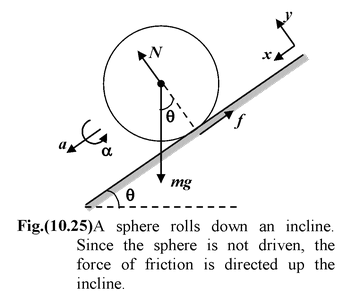
Since the sphere is not driven by a chain or an axle the force of friction must be directed backward, up the slope. If there is no slipping, the point of contact is simultaneously at rest and so the friction is static. The linear acceleration a of the c.m. and the angular acceleration α are assumed as shown in the figure(10.25). Applying Newon’s Second Law |
|
ΣFx = ma Mg sin θ - f = Ma (i)
Στ = IαfR = Iα = 2/5MR2α(ii)
Since the sphere rolls without slipping, the speed of the center is v = ωR.
By differentiating it with respect to time, we get
a = αR.(iii)
Solving equation (i), (ii) & (iii)
we getf = 2/5 Ma(iv)
anda = 5/7 g sin θ (v)
(b)Substituting (v) into (iv) yields
f = 2/7 Mg sin θ(vi)
We use equation (vi) to find the minimum coefficient of friction required for the sphere to roll without slipping.
By definition, f = μN where N = M g cosθ. Combining this with equation (vi) we have
μ = 2/7 tanθ
If the coefficient of static friction is less than this value, the sphere will slip as it rolls down the incline.
Example 10.18
|
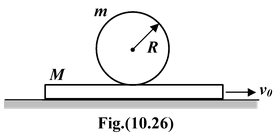
A sphere of mass m and radius R is placed at rest on a plank of mass M which is placed on a smooth horizontal surface as shown in the figure(10.26). The coefficient of friction between the sphere and the plank is μ. At t = 0, a horizontal velocity v0 is given to the plank. Find the time after which the sphere starts rolling. |
|
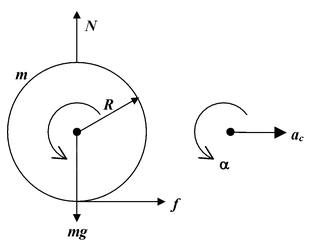
Solution
Sphere :ac = f/m = μg
α =
After time t vc = act = μgt
ω = αt =
The velocity of the point of contact is v = vc + ωR = μgt + μgt = μgt |
|
Planck :
Retardation a =
Instantaneous velocity v = v0 -
Condition of pure rolling
v =
or t =
|
|
Example 10.19
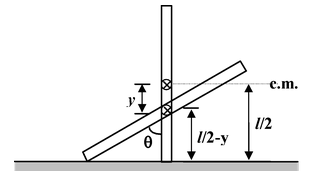
A stick of length l and mass M , initially upright on a frictionless floor, starts falling. Find the velocity of its centre of mass when it touches the floor. Describe the trajectory of the centre of mass.
|
Solution Initial energy of the system E0 = Mg Energy of the system at some later instant E = K + U
K =
|
|
U =
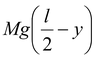
Where ω is the angular velocity of the rod about its centre of mass, and v is the vertical velocity of the centre of mass.
Using conservation of energy ,we get
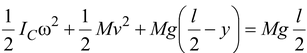 (1)
(1)
Here,Ic =
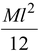
Relation between ω and v
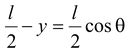
differentiating w.r.t. time , we get

The centre of mass falls vertically downwards.

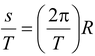
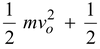 (mR2) ω
2
(mR2) ω
2
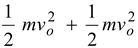
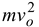
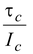 =
=
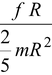 =
=