
Trigonometric Identities
Trignometric functions of Class 11
- Sin nπ = 0 if n∈I
- Cos nπ/2 = 0 if n is an odd integer
- cos (nπ + θ) = (-1)n cos θ, n ∈ I
- sin (nπ + θ) = (-1)n sin θ, n ∈ I
- Cos (nπ/2 +θ) = (−1)(n + 1)/2 Sinθ, if n is odd integer
- Sin (nπ/2 +θ) = (−1)(n-1/2) Cosθ, if n is odd integer
For Any Three Angles A,B,C
(a) sin (A+B+C) = sin A cos B cos C + sin B cos C cos A + sin C cos A cos B − sin A sin B sin C
(b) cos (A+B+C) = cos A cos B cos C – cos A sin B sin C - cos B sin A sin C – cos C sin A sin B
(c) tan (A+B+C) = 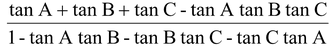
(d) cot (A+B+C) = 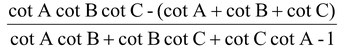
Greatest And Least Values of a cosθ + b sinθ
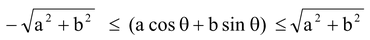
Some Important Identities
If A+B+C = π then
- sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C
- cos 2A + cos 2B + cos 2C = -1 –4 cos A cos B cos C
- sin A + sin B + sin C = 4 CosA/2 cos B/2 cosC/2
- cos A + cos B + cos C = 1 + 4 sin A/2 sin B/2 sin C/2
- tan A + tan B + tan C = tan A tan B tan C
- cot A cot B + cot B cot C + cot C cot A = 1
- tan A/2 tan B/2 + tan B/2 tan C/2 + tan C/2 tan A/2 = 1
- cot A/2 + cot B/2 + cot C/2 = cot A/2. cot B/2. cot C/2
Two Useful Identities
-
cos α + cos β + cos γ + cos (α+β+γ) = 4
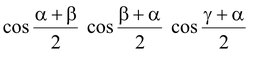
-
sin α + sin β + sin γ - sin (α+β+γ) = 4
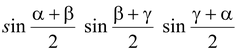
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2026 Physicswallah Limited All rights reserved.