Laws of Exponents Overview, Rules, Examples, Tips
Laws of exponents include product, quotient, power, zero, negative exponents, and distributive properties for multiplying and dividing bases. Check out this article to know all laws of exponents.
Neha Tanna5 Jun, 2025
Share
Laws of Exponents: The laws that are used to simplify expressions using exponents are known as exponent rules. Using the principles of exponents, a variety of arithmetic operations, including addition, subtraction, multiplication, and division, can be easily completed in short stages. These guidelines also aid in the simplification of complex powers of numbers that contain roots, fractions, and decimals.
Now that we have a better understanding of the various exponent rules, let's look at some examples using various base and exponent numbers.What are Laws of Exponents?
Simplifying formulas containing exponents is made easier by exponent rules, commonly referred to as the "laws of exponents" or the "properties of exponents." These rules are useful for simplifying expressions whose exponents are fractions, decimals, irrational numbers, or negative integers. For instance, we can quickly solve 34 × 32 by applying one of the exponent laws, which states that am × a = am + n. By applying this approach, we can obtain the answer by simply adding the exponents, leaving the base unchanged: 34 × 32 = 34 + 2 = 36. Likewise, the exponent rules provide an easy way to solve expressions with larger exponent values. This is the exponent rules list.- a 0 = 1
- a 1 = a
- a m × a n = a m+n
- a m / a n = a m−n
- a −m = 1/a m
- (a m ) n = a mn
- (ab) m = a m b m
- (a/b) m = a m /b m
Also Read-
| Riddles for Kids | Multiplication | Indoor Games for Kids |
| Subtraction | Maths Puzzles | Laws of Exponents |
Laws of Exponents
The laws of exponents, or properties of exponents, are another name for the many exponent rules. In the part before this one, the laws of exponents were already covered. The majority of them go by specific names, like the negative rule of exponents, the quotient rule of exponents, the zero rule of exponents, and so on.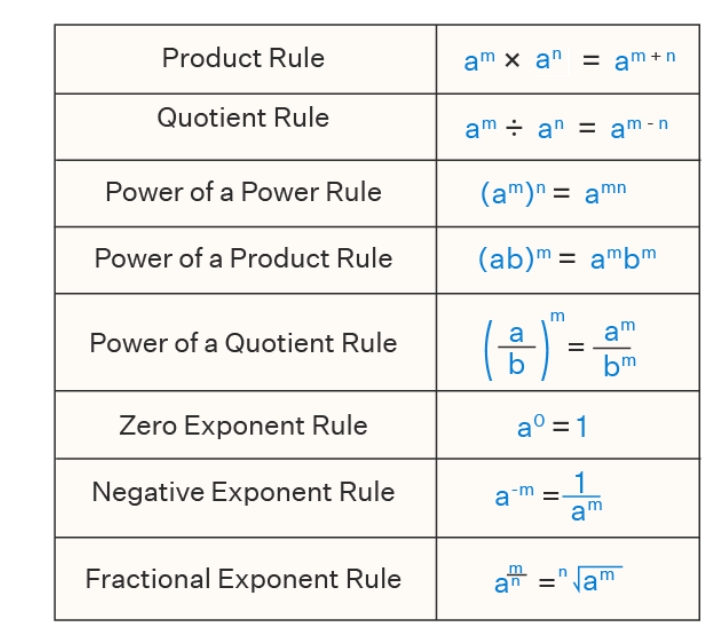
Let us learn each of these in detail now.
Product Law of Exponents
Expressions with identical bases are multiplied using the exponent product rule. The rule reads: "To multiply two expressions with the same base, add the exponents while keeping the base the same." Adding exponents with the same base is required by this rule. In this case, the rule can be applied to simplify two expressions that have a multiplication operation. Observe the following example.| Using the Product Rule of Exponents | Without Using the Rule |
| 2 3 × 2 5 = 2 (3 + 5) = 2 8 | 2 3 × 2 5 = (2 × 2 × 2) × (2 × 2 × 2 × 2 × 2) = 2 8 |
Read More: What is Temperature?
Quotient Law of Exponents
Expressions with the same bases can be divided using the quotient law of exponents. It states, "To divide two expressions with the same base, subtract the exponents while keeping the base same." This helps to solve an equation without having to carry out the division procedure. The two expressions need merely share the same base in order to be considered. Here is an example.| Using the Quotient Law of Exponents | Without Using the law |
| 2 5 /2 3 = 2 5 - 3 = 2 2 | 2 5 /2 3 = (2 × 2 × 2 × 2 × 2)/ (2 × 2 × 2) = 2 2 |
Zero Law of Exponents
When an expression's exponent is zero, the zero law of exponents is applied. It states that "Any number (other than 0) raised to 0 is 1." Keep in mind that 00 is an ambiguous form and is not defined. This will clarify for us that the value of a zero exponent is always equal to one, regardless of the base. Here is an example of zero law of exponents.| Using the Zero Law of Exponents | Without Using the Law |
| 2 0 = 1 | 2 0 = 2 5 - 5 = 2 5 /2 5 = (2 × 2 × 2 × 2 × 2)/(2 × 2 × 2 × 2 × 2) = 1 |
Negative Law of Exponents
When an exponent is a negative number, the negative law of exponents is applied. It states that "To convert any negative exponent into positive exponent, the reciprocal should be taken." With the sign of the exponent values changed, the expression is moved from the numerator to the denominator. Here is an example of negative law of exponents.| Using the Negative Law of Exponents | Without Using the Law |
| 2 -2 = 1/(2 2 ) | 2 -2 = 2 0-2 = 2 0 /2 2 = 1/(2) 2 |
Power of a Power Law of Exponents
Expressions of the form (am)n can be made simpler by applying the 'power of a power law of exponents'. It states, "When we have a single base with two exponents, just multiply the exponents." One exponent is available in preference to the other. It is convenient to multiply these to get a single exponent. Here is an example of power of power law of exponents.| Using the Power of a Power Law of Exponents | Without Using the Law |
| (2 2 ) 3 = 2 6 | (2 2 ) 3 =(2 2 )(2 2 )(2 2 ) =(2 · 2) (2 · 2) (2 · 2) = 2 6 |
Power of Product Rule of Exponents
To find the outcome of a product raised to an exponent, apply the "power of a product rule of exponents." It states, "Distribute the exponent to each multiplicand of the product." Here is an example of power of product rule of exponents.| Using the Power of Product Rule of Exponents | Without Using the Rule |
| (xy) 3 = x 3 .y 3 | (xy) 3 =(xy).(xy).(xy) = (x.x.x).(y.y.y) x 3 .y 3 |
Power of a Quotient Rule of Exponents
To find the outcome of a quotient raised to an exponent, apply the power of a quotient rule of exponents. It states, "Distribute the exponent to both the numerator and the denominator." In this case, the exponents for the two bases are the same but the bases are different. Here is an example of power of a quotient rule of exponents given above.| Using the Power of a Quotient Rule of Exponents | Without Using the Rule |
| (x/y) 3 = x 3 /y 3 | (x/y) 3 = x/y . x/y . x/y = x 3 /y 3 |
Read More: What is Photosynthesis?
Fractional Exponents Rule
According to the rule of fractional exponents, a1/n = n−a. i.e., radicals are the outcome of a fractional exponent. As an instance, a1/2 = √a, a1/3 = ∛a, and so on. When dealing with complex fractional exponents such as am/n, this rule is further expanded. Utilising the power of a power rule of exponents, which we have already covered in a section, a m/n = (a m ) 1/n Now, by using the fractional exponents rule, this fractional power turns into a radical. a m/n = n √(a m ) This is also used as an alternate form of the fractional exponents rule. Thus, this fractional exponents rule is defined in two ways:- a 1/n = n √a
- a m/n = n √(a m )
Exponent Rules Chart
A visual like the one below can be used to summarise the previously discussed exponent rules.| Name of Exponent Rules | Rule |
| Zero Exponent Rule | a 0 = 1 |
| Identity Exponent Rule | a 1 = a |
| Product Rule | a m × a n = a m+n |
| Quotient Rule | a m /a n = a m-n |
| Negative Exponents Rule | a -m = 1/a m ; (a/b) -m = (b/a) m |
| Power of a Power Rule | (a m ) n = a mn |
| Power of a Product Rule | (ab) m = a m b m |
| Power of a Quotient Rule | (a/b) m = a m /b m |
Tips on Exponent Rules:
If the exponent of a fraction is negative, we use its reciprocal to make it positive; for example, (a/b)-m = (b/a)m. This rule can be used to change a radical into an exponent: a1/n = n^aJoin Maths Online Classes for Kids Now!!
Laws of Exponents FAQs
What is 7 as an exponent?
In arithmetic and algebra, the seventh power of a number n is the result of multiplying seven instances of n together. So: n7 = n × n × n × n × n × n × n.
What is the zero exponent rule?
One rule of exponents is the zero-exponent rule. The zero exponent rule simply states that any nonzero number raised to the power of 0 is equal to 1. The Zero Exponent Rule. a 0 = 1, a ≠ 0. 0 0 is considered undefined.
What is 10 the first power?
10 to the power 1.
What is the 5th law of exponents?
The 5th Law of Exponents states that when a polynomial with a power 'a' is raised to a power 'b', then the final power of the exponents is the value of the product of the exponents, i.e., a * b. This video states the 5th Law of Exponents and shows how to solve problems relating to it.
What is 4 called in math?
There are two common prefixes to express the number 4 used in math. They are tetra and quad,
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.