Binding Energy And It's Application

Binding Energy

Binding energy is also known as Separation Energy.

As we know, in the nucleus protons and neutrons are held together by a very strong attractive force called Nuclear force, where protons and neutrons are collectively known as nucleons. Therefore a large amount of energy is required to separate the nucleons from this force.

“Binding Energy is defined as the energy required to break up a nucleus into its constituent nucleons”.

Binding energy can also be understood in terms of Einstein’s mass-energy equivalence.

The mass of a nucleus is always less than the sum of the individual masses of protons and neutrons. When nucleons are brought together to form a nucleus, a certain amount of mass disappears. The difference between the sum of masses of nucleons and the actual mass of a nucleus is called disappearing mass. This mass difference is called a “Mass Defect”. This disappeared mass is now converted into energy, which binds nucleons together in a nucleus.

“ Binding Energy can also be defined as, the energy with which nucleons are bound in a nucleus”.

Types of Binding Energy:

1. Electron Binding Energy - Ionization Energy: Electron Binding Energy commonly known as Ionization Energy , is the energy required to remove an electron from the outermost orbit.
2. Atomic Binding Energy: Atomic Binding Energy is the energy required to break down an atom into free electrons and a nucleus.
3. Nuclear Binding Energy: Nuclear Binding Energy is the energy required to break up a nucleus into free unbound neutrons and protons.

Mathematical Expression for Calculating the Binding Energy:

Consider a Nucleus , X _Z ^A

Let, M = Actual mass of a Nucleus.

Z = Atomic Number.

A = Mass Number.

m _p = Mass of Proton.

m _n = Mass of Neutron.

Sum of masses of Nucleons = Zm _p + (A - Z)m _n

Mass Defect (m) = Sum of masses of Nucleons - Actual mass of a Nucleus

Δ m = [Zm _p + (A - Z)m _n ] - M

Now, mass is converted into Binding Energy:

Binding Energy ( Δ E _b ) = Δ m c ²

c = speed of Light

Expression for Binding Energy:

Δ E _b = {[Zm _p + (A - Z)m _n ] - M} c ²

In MeV, ( Δ E _b ) = m 931.49 MeV

• For the stability of the nucleus let us discuss Binding Energy per Nucleon.
• “Binding Energy per Nucleon is the average energy required to extract one nucleon from the nucleus”.

​ In simple words, “It is the ratio of Binding Energy of Nucleus to the number of Nucleons”.

Expression for Binding Energy per Nucleon:

Δ E _b /A = 1/A {[Zm _p + (A - Z)m _n ] - M} c ²

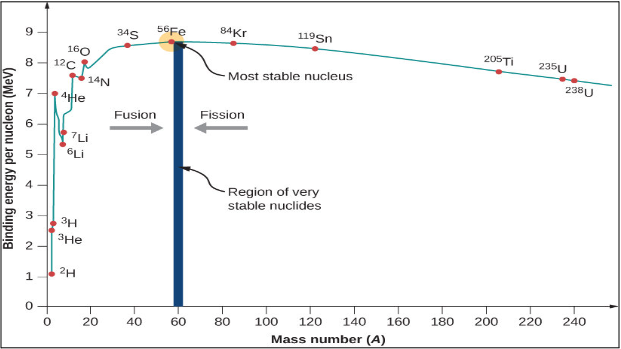
• Binding Energy per Nucleon of a nucleus gives the quantitative measure of its stability.
• For Example we consider the He ₂ ⁴ nuclide which is made up of two protons and two neutrons for which Binding Energy comes out to be 28.3 MeV, we can say that the energy required to break up a He ₂ ⁴ nucleus into its constituent nucleons, about 28 MeV energy must be spent. This Binding Energy per nucleon for He ₂ ⁴ is approximately 7 MeV. Hence stability of a nucleus depends upon its Binding Energy.

• Greater the Binding Energy per Nucleon more stable the Nucleus.

• The Total Binding energy of a nucleus is positive and is not a sufficient condition for its stability. For a nucleus to be stable its mass should be less than that of the sum of masses of any other combinations of its constituent protons or neutrons whether free or bound in small groups.
• For lighter nuclei like H ₁ ¹ , H ₁ ² , and H ₁ ³ Binding energy per Nucleon is less hence, they are least stable.
• Binding energy per nucleon for Fe ₂₆ ⁵⁶ is 8.8 MeV/Nucleon hence, it is most stable.
• From 2<A<20 nuclides like He ₂ ⁴ , Be ₄ ⁸ , C ₆ ¹² , O ₈ ¹⁶ , Ne ₁₀ ^20, and Mg ₁₂ ²⁴ have sharp increases in Binding Energy as compared to their neighbors which indicates that they are more stable than their neighboring nuclei.
• For heavy nuclei the Binding energy per nucleon decreases to 7.6 MeV/Nucleon for U ₉₂ ²³⁵
• The decrease in Binding Energy per Nucleon for heavier nuclides is due to an increase in the force of repulsion among the protons, as their number increases in heavy nuclides.
• The average Binding Energy per nucleon of nuclides heavier than Uranium is still smaller. As they are unstable and hence radio-active.

Applications:

• Binding Energy is used to determine whether Fusion or Fission will occur. For elements lighter than Iron-56 undergo Fusion, whereas elements heavier than Iron-56 undergo Fission.
• Splitting a heavy nucleus into two medium-sized ones, each of the new nuclei will have more Binding energy per nucleon than the original nucleus did. The extra energy will be given off. If Uranium nucleus U ₉₂ ²³⁵ is broken into two smaller nuclei, the Binding energy difference per nucleon is about 0.8 MeV. Splitting a heavy nucleus into smaller nuclei is called Nuclear Fission . The energy released in Fission is several million times more than that is released in chemical changes because the Binding energy of nuclei involved in the process of fission are much more than the Binding energy of electrons involved in the chemical process.
• Joining two light nuclei together to form a single nucleus of medium size, a single new nucleus has more Binding energy per Nucleon than the two light nuclei. If two H ₁ ² deuterium nuclei combine to form a He ₂ ⁴ Helium nucleus, over 23 MeV is released. Such a process is called Nuclear Fusion . Nuclear Fusion is the main energy source of the sun and the other stars.