CBSE Class 10 Maths Notes Chapter 12 Areas Related to Circles
Here, we have provided CBSE Class 10 Maths Notes Chapter 12. Students can view these CBSE Class 10 Maths Notes Chapter 12 Area Related to Circles before exams for better understanding of the chapter.
Neha Tanna22 Apr, 2024
Share
CBSE Class 10 Maths Notes Chapter 12: Get all of the class 10 notes on a topic about circles here. This page contains the following circle-related concepts: area, circumference, segment, sector, angle, length, and area for a circle's sector. Additionally, some plane and solid figure areas' visualisation is covered here.
We will study how to calculate the circumference, and length of an arc in a sector, areas of circles, areas of segments and sectors of circles, and other related concepts in the Class 10 chapter "Areas Related to Circles." A circle is a figure with two dimensions. All of the points on this curving form are equally spaced from the center. Now let's explore how to locate regions connected to the circle in this post.CBSE Class 10 Maths Notes Chapter 12 PDF
The solutions are constructed step-by-step to emphasize the key shortcuts and formulas. These Circles-Related Class 10 Notes are thoughtfully crafted to offer students an exceptional educational experience and accelerate their comprehension of the material. Students can use the free PDF versions of the answers to the key problems in CBSE Class 10 Maths Notes Chapter 12 Areas Related to Circles.CBSE Class 10 Maths Notes Chapter 12 PDF
CBSE Class 10 Maths Notes Chapter 12
Area of a Circle
The area of a circle is πr 2 , where π=22/7 or ≈ 3.14 (can be used interchangeably for problem-solving purposes) and r is the radius of the circle. π is the ratio of the circumference of a circle to its diameter. Example: Find the area of a circle with radius = 7cm. Solution: Given, the radius of the circle = 7cm By the formula we know; Area of circle = πr 2 = π(7) 2 = (22/7) (7) 2 = 154 sq. cm.Circumference of a Circle
The circumference of a circle is the distance covered by going around its boundary once.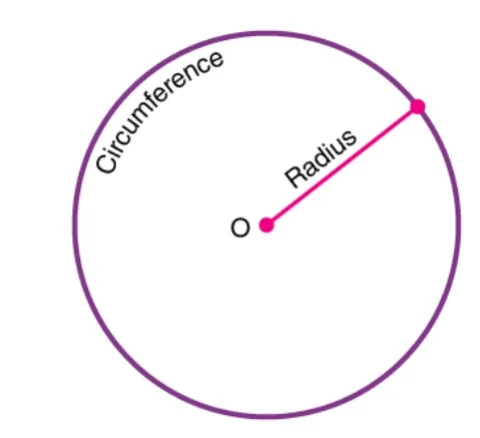
The perimeter of a circle has a special name: Circumference, which is π times the diameter which is given by the formula;
Circumference of a circle = 2πr.
Example: The circumference of a circle whose radius is 21cm is given by;
C = 2πr
= 2 (22/7) (21)
= 132 cm
CBSE Class 10 Syllabus 2024-25
Segment of a Circle
A circular segment is a region of a circle that is “cut off” from the rest of the circle by a secant or a chord.Sector of a Circle
The area of a circle bounded by two radii and an arc is called a sector or circle sector. The term "minor sector" refers to the smaller area and the "major sector" to the bigger region.Angle of a Sector
The angle of a sector is the angle that is enclosed between the two radii of the sector.Area of a Sector of a Circle
The area of a sector is given by( θ/360°) × π r 2where ∠ θ is the angle of this sector(minor sector in the following case) and r is its radius
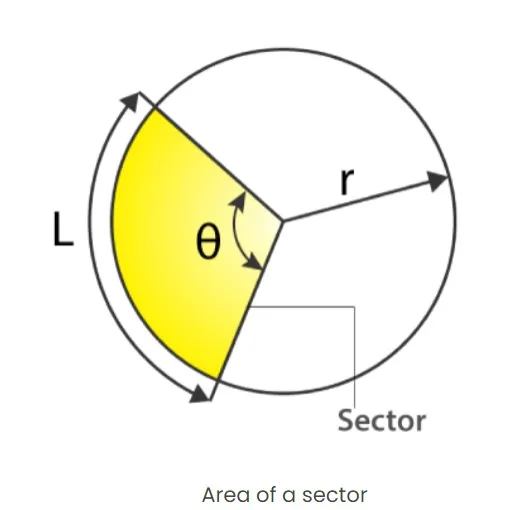Example: Suppose the sector of a circle is 45° and the radius is 4 cm, then the area of the sector will be:
Area = (θ/360°) × πr
2
= (45°/360°) × (22/7) × 4 × 4
= 44/7 sq. cm
The length of the arc of a sector can be found by using the expression for the circumference of a circle and the angle of the sector, using the following formula:
L = ( θ/360°) × 2 π rWhere θ is the angle of the sector and r is the radius of the circle.
Area of a Triangle
The area of a triangle is, A r e a =(1/2) × b a s e × h e i g h t If the triangle is equilateral then, Area (√ 3/4)× a 2 where “ a” is the side length of the triangle.Area of a Segment of a Circle
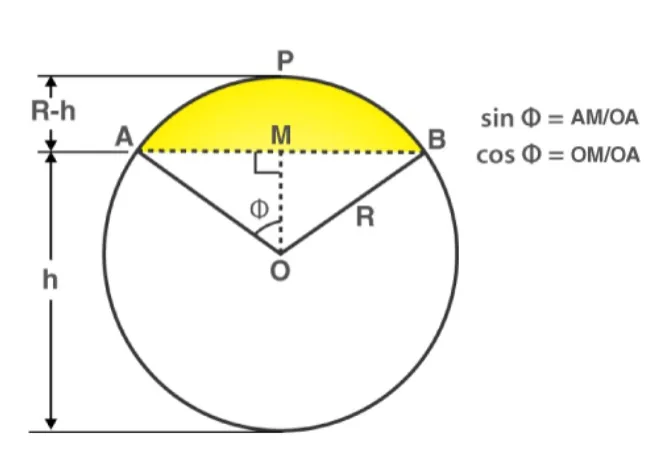Area of segment APB (highlighted in yellow)
= (Area of sector OAPB) – (Area of triangle AOB)
=[(∅/360°) × π r 2 ] – [(1/2) × A B ×OM][To find the area of triangle AOB, use trigonometric ratios to find OM (height) and AB (base)] Also, the area of segment APB can be calculated directly if the angle of the sector is known using the following formula.
= [(θ/360°) × π r 2 ] – [ r 2 ×sin θ/2 × cos θ/2 ]Where θ is the angle of the sector and r is the radius of the circle.
Visualizations
Areas of Different Plane Figures
– Area of a square (side l) = l 2 – Area of a rectangle = l × b , where l and b are the length and breadth of the rectangle – Area of a parallelogram = b × h , where “ b” is the base and “ h” is the perpendicular height.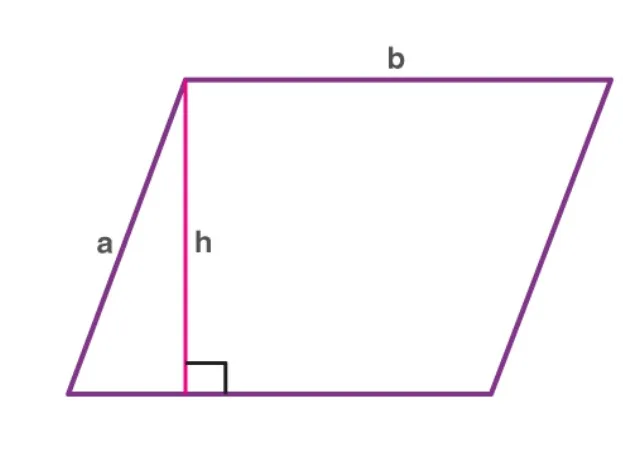
Area of a trapezium
=[
(a+b)×
h]/2
,
where
a
&
b
are the lengths of the parallel sides
h is the trapezium height
The area of a rhombus
=
pq/2,
where
p
&
q
are the diagonals.
Benefits of CBSE Class 10 Maths Notes Chapter 12
- Domains Associated with Circles Your Class 10 Notes can help you anticipate the kinds of questions that might be asked on the test.
- For a better comprehension of the subjects, the solutions are divided into several exam portions.
- With our revision notes, you can grasp the subjects more clearly and simply. Our solutions are well-structured and free of errors.
CBSE Class 10 Maths Notes Chapter 12 FAQs
What is the area related to the circle in maths 10th notes?
A segment of a circle is the region bounded by an arc and a chord, including the arc and the chord.
What is the formula related to the area related to a circle?
Area of circle = πr. Circumference of circle = 2πr. Length of an arc of a sector = L= (θ/360°)×2πr. Area of a sector of circle = (θ/360°)×πr.
Is areas related to circles easy?
Overall, areas related to circles can be considered a moderately difficult chapter in mathematics.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
