Trigonometric Equations Formula: Solve with Ease

Trigonometry , derived from the Greek words "trigonon" (meaning triangle) and "metron" (meaning measure), is a branch of mathematics that explores the relationships between the lengths and angles of the sides of triangles. In trigonometry, equations are often encountered, known as trigonometric equations, which involve one or more unknown angles expressed as ratios of trigonometric functions such as sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (cosec).

For instance, an example of a trigonometric equation is "cos^2(x) + 5sin(x) = 0." The solutions to a trigonometric equation are all the possible values of the unknown angles that satisfy the equation's conditions. These solutions represent specific angle measurements that make the equation true.

Take a look at a right-angled triangle, as illustrated in Figure 1. In this figure, you can see that angle ∠A is formed as an acute angle.

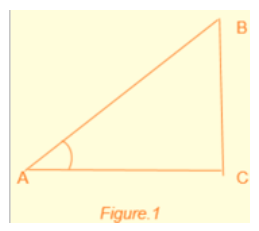
From the figure, the following trigonometric ratios can be deducted.

Each of these trigonometric ratios can be calculated at various angles. Table 1 provides some common reference angles for each of these ratios. By using these standard angles as a foundation, we can extend the evaluation of trigonometric ratios to any angle.

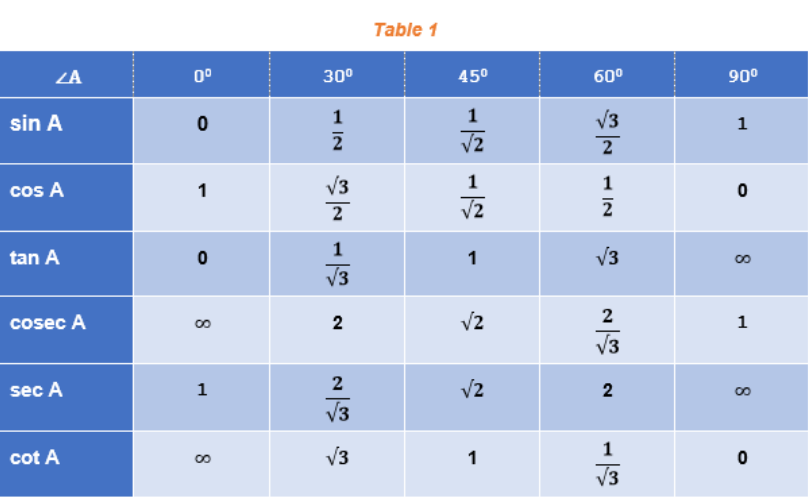
Note: By referring to Table 1 above, it's evident that as angle ∠A increases from 0° to 90°, the value of sin A increases from 0 to 1, while cos A decreases from 1 to 0.

Also check: Trigonometry Formula for Class 10

Trigonometric Ratios of Complementary Angles

As shown in Figure 1, it's evident that ∠A + ∠B = 90° or ∠B = 90° – ∠A. Therefore, let's examine the sine value of ∠B, denoted as sin B = sin (90° – ∠A) = AC/AB. Remarkably, AC/AB is equivalent to cos A.

In summary, we can state that sin (90° – ∠A) = cos A. Similarly, we can define other trigonometric ratios for complementary angles as follows:

1. sin (90° – ∠A) = cos A
2. cos (90° – ∠A) = sin A
3. tan (90° – ∠A) = cot A
4. cot (90° – ∠A) = tan A
5. sec (90° – ∠A) = cosec A
6. cosec (90° – ∠A) = sec A

Identities in Trigonometry

In Figure 1, it's evident that the right triangle ABC exhibits the Pythagorean property, expressed as AB^2 = AC^2 + BC^2.

By dividing both sides of the equation by AB^2, we obtain the equation 1 = cos^2A + sin^2A. This equation represents a fundamental identity in trigonometry. Additionally, we can derive other identities, which are listed below:

sin ² A + cos ² A = 1

sec ² A – tan ² A = 1

cosec ² A – cot ² A = 1

These identities are essential tools in trigonometric calculations and relationships.

Also Check - Cube Root Formula

Trigonometric Formulas

It's crucial to remember several important formulas when tackling various trigonometric problems and scenarios. Here are a few of them:

cos (2nπ + x) = cos x

sin (2nπ + x) = sin x

cos (-x) = cos x

sin (-x) = – sin x

cos (x + y) = cos x cos y – sin x sin y

cox (x – y) = cos x cos y + sin x sin y

sin (x + y) = sin x cos y + cos x sin y

sin (x – y) = sin x cos y – cos x sin y

cos 2x = cos2x – sin2x = 2 cos2x – 1 = 1 – 2 sin2 x

cos x + cos y = 2 cos{(x+y)/2} cos{(x-y)/2}

cos x – cos y = -2 sin{(x+y)/2} sin{(x-y)/2}

sin x + sin y = 2 sin{(x+y)/2} cos{(x-y)/2}

sin x – sin y = 2 cos{(x+y)/2} sin{(x-y)/2}

2 cos x cos y = cos (x + y) + cos (x – y)

-2 sin x sin y = cos (x + y) – cos (x – y)

2 sin x cos y = sin (x + y) + sin (x – y)

2 cos x sin y = sin (x + y) – sin (x – y)

cos(π – x) = -cos x

cos(π + x) = -cos x

sin(π – x) = sin x

sin(π + x) = -sin x

cos(2π – x) = cos x

sin(2π – x) = – sin x

cos (π/2 + x) = – sin x

sin (π/2 + x) = cos x

cos 3x = 4 cos3x – 3 cos x

sin 3x = 3 sin x – 4 sin3x

Radian measure = degree measure x π/180

Degree measure = radian measure x 180/π

Also Check - Probability Formula

Trigonometric Equations and Its Solutions

Trigonometric equations refer to mathematical equations that involve trigonometric functions such as sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). These equations typically contain one or more unknown angles, and the goal is to find the values of these angles that satisfy the equation.

The solutions to trigonometric equations are the specific angle measurements that make the equation true. These solutions are often expressed in degrees or radians, depending on the context. Solving trigonometric equations is a fundamental part of trigonometry and is used in various fields such as physics, engineering, and geometry to analyze and model real-world problems involving angles and periodic phenomena.

Trigonometric equations can vary in complexity, and there are different techniques and methods to solve them, including algebraic manipulations, identities, and graphical approaches. The solutions to these equations play a significant role in understanding and predicting periodic behavior, waveforms, and oscillatory systems.