The concept of center of gravity (COG), center of mass (COM), and centroid are fundamental in engineering mechanics and play a crucial role in understanding the stability, equilibrium and motion of rigid bodies.
Center of Gravity (COG)
-
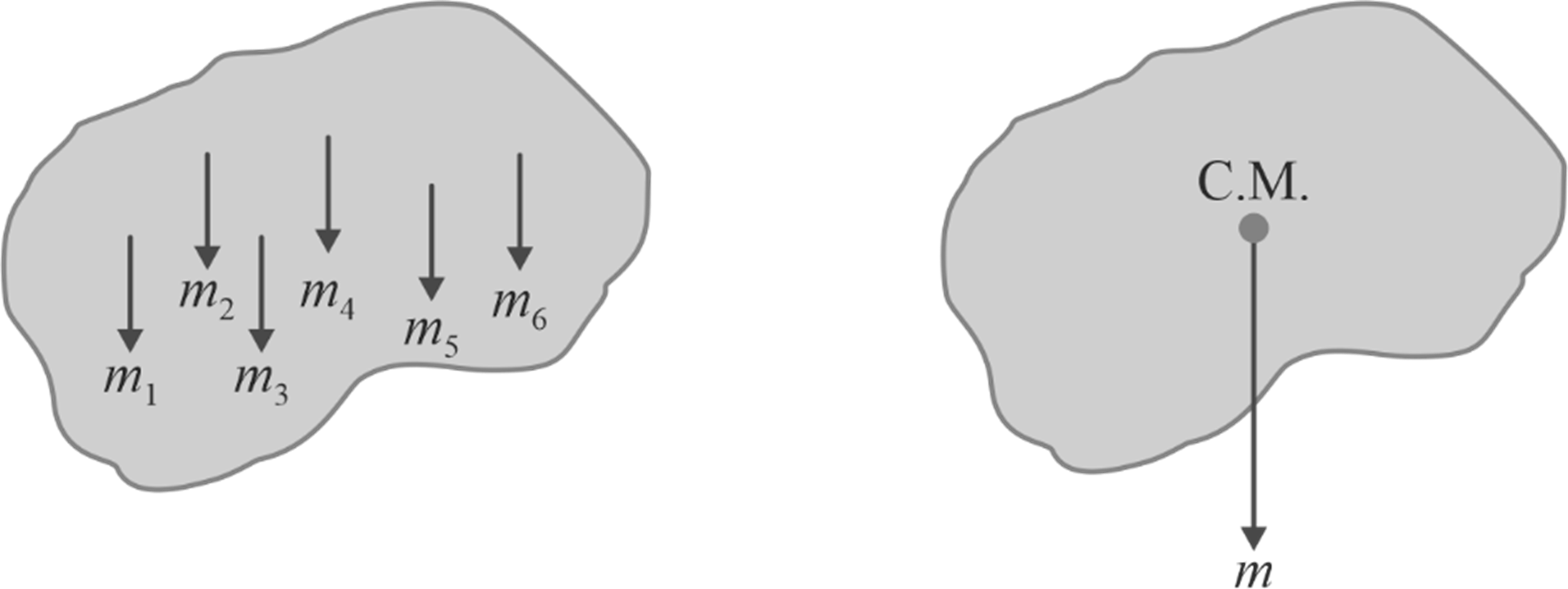
An object is made up of countless tiny particles, each incredibly small. These particles experience the force of gravity, which pulls them downward vertically, as illustrated in Figure.
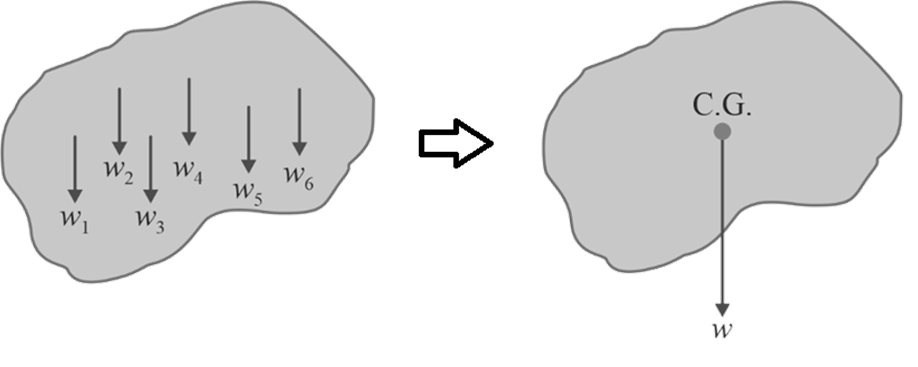
- COG is an imaginary point where the weight of the body can be assumed to be concentrated. In simple words, "it is that point within or outside a body through which the resultant of the distributed parallel gravity force passes, no matter how the object is positioned in space . "
- The symbol 'G' is commonly used to represent the center of gravity for three-dimensional rigid objects.
Location the Center of Gravity
-
Imagine a flat plate with a consistent thickness (t), positioned on the xy plane as shown in the figure below. This plate can be broken down into small components, each carrying a weight like w
1
, w
2
, and so on. These components are positioned at specific coordinates from origin such as (x
1
, y
1
), (x
2
, y
2
), and so forth.
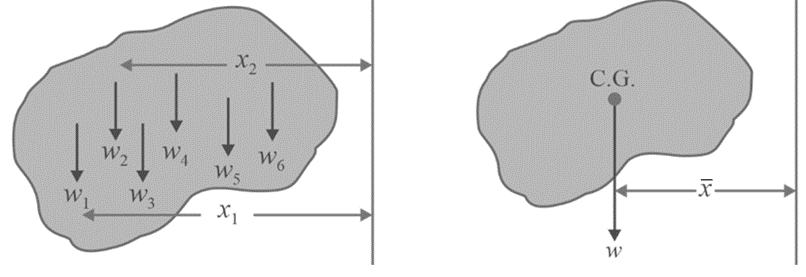
- To figure out the location of the centre of gravity on any object, we use a rule called the principle of moments (Varignon’s theorem).
Moment due to resultant weight about Y axis = net moment due to weight components about Y axis
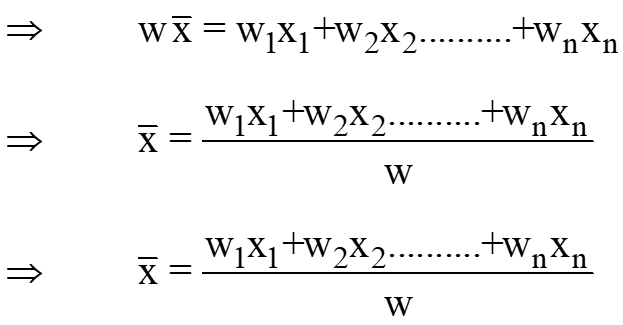
-
The coordinates of the center of gravity relative to the origin may be expressed as;
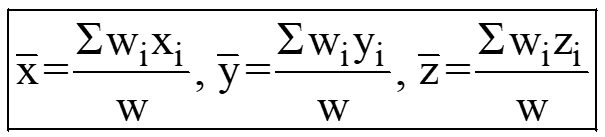
Mathematically, we can also represent the above expressions in the following manner:;
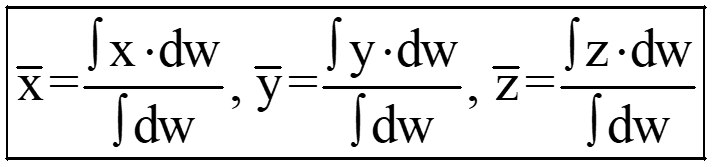
Center of Mass (COM)
-
“The center of mass (COM) of an object is the point at which the entire mass of the object is considered to be concentrated.”
- The center of mass is crucial for understanding acceleration's impact on a body. The resulting force aligns with acceleration and acts through the center of mass.
-
By using principle of moments, the coordinates of the center of mass relative to the origin may be expressed as;
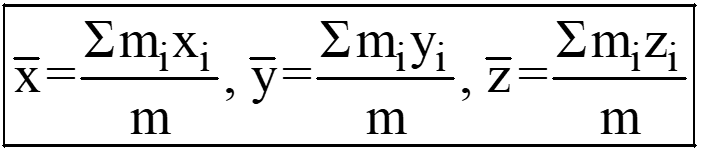 Mathematically, we can also represent the above expressions in the following manner:
Mathematically, we can also represent the above expressions in the following manner:
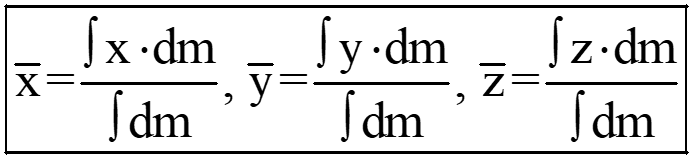
- Centre of mass lies at centre of gravity in a uniform gravitational field.
Centroid
- Centroid is a concept often encountered in engineering design and analysis, particularly in the study of structures and materials. It represents the central point of a 2D, or 3D shape, influenced by the location and size of each tiny area or volume part.
- “A centroid is a point either inside or outside a shape where the total area of the shape can be considered to be concentrated.”
-
The coordinates of the centroid of a plane area relative to the origin may be expressed as;
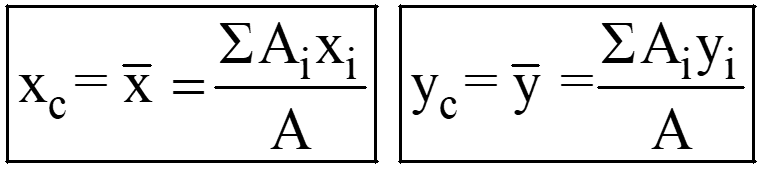
Mathematically, we can also represent the above expressions in the following manner:
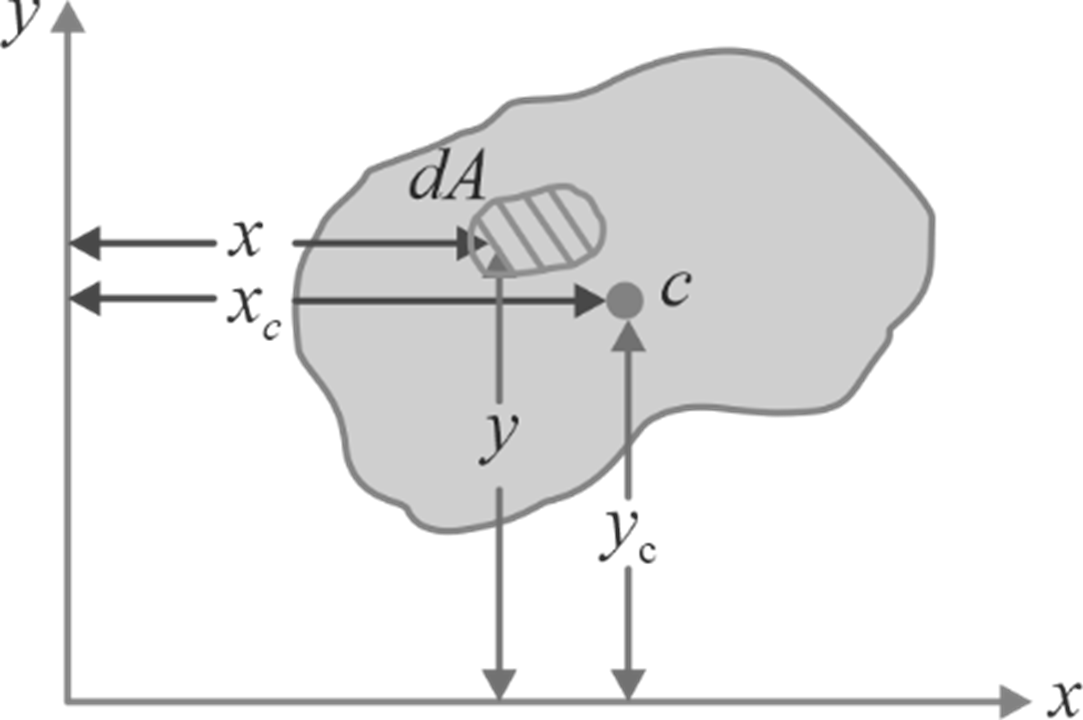
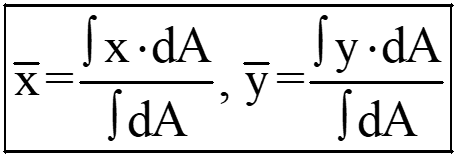
Note: When finding the centroid of a line or a volume, we use the same formula as before, but instead of A, we use L for lines or V for volumes in the expression mentioned above.
- If the density of the body is uniform throughout, then the centroid coincides with the center of mass.
-
If an area or volume exhibits symmetry about any axis, the centroid will always lie on that axis of symmetry.
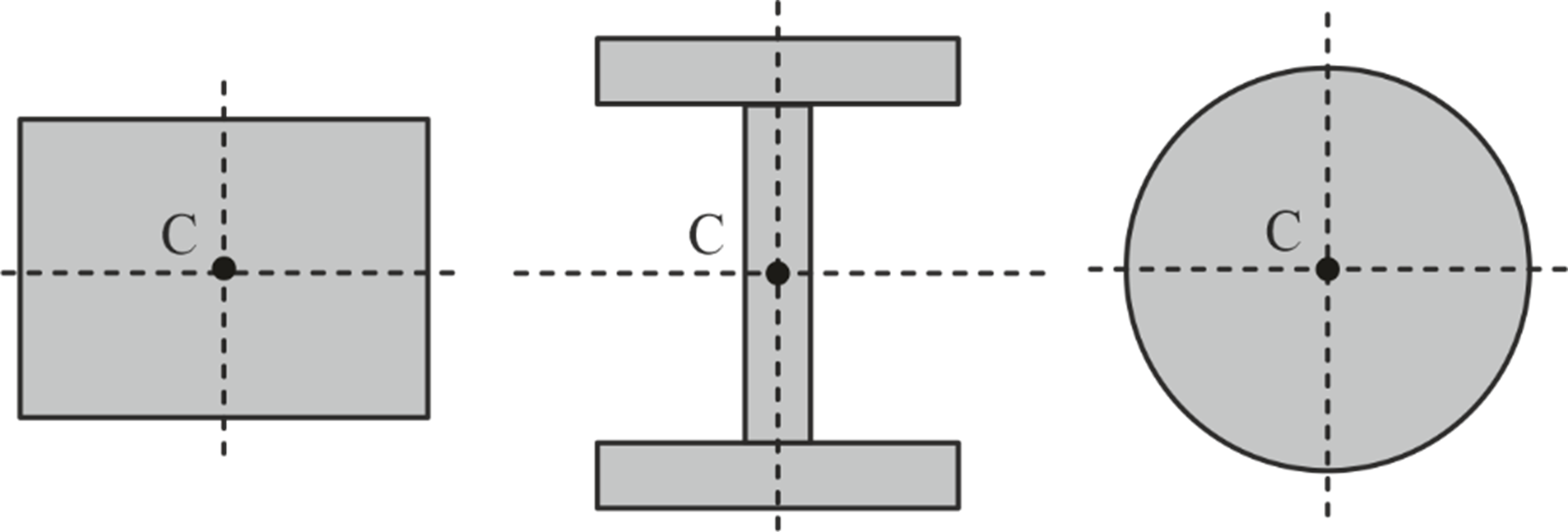
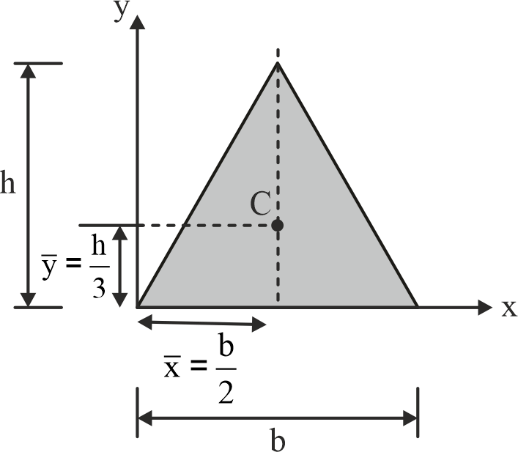
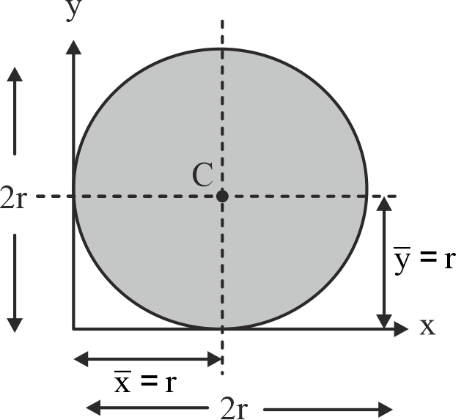
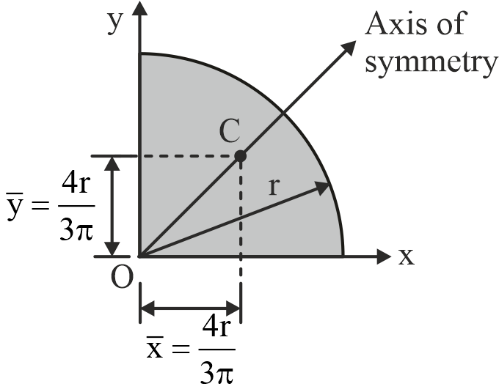
Centroid of Some Common Geometrical Shapes
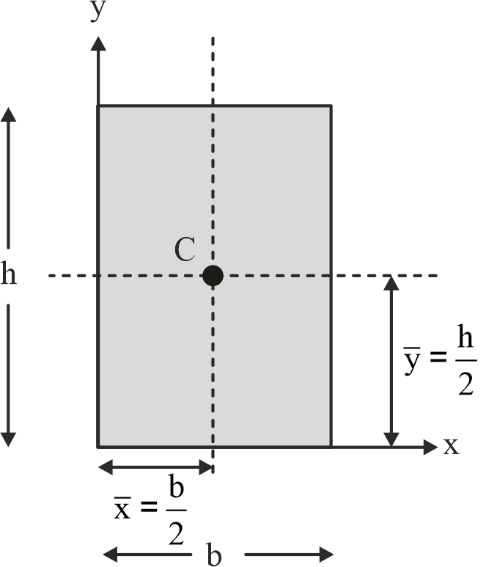
|
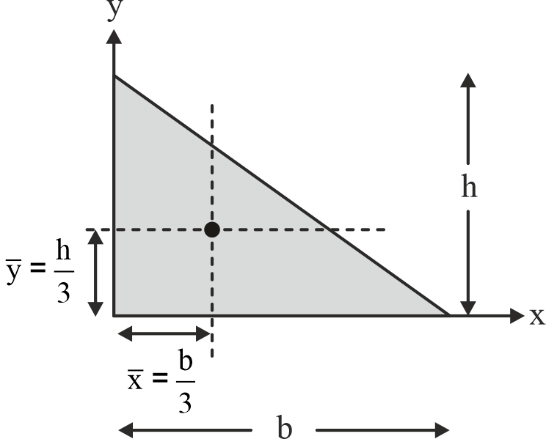
|
|
|
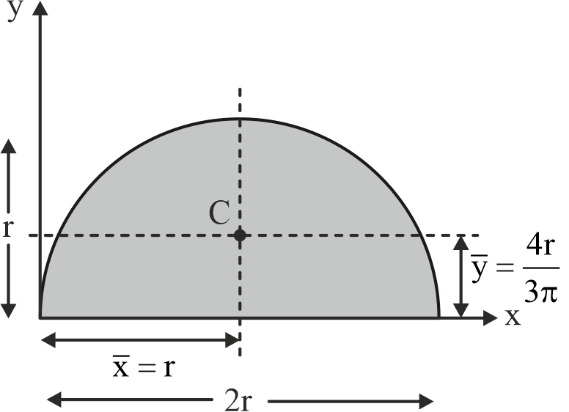
|
|
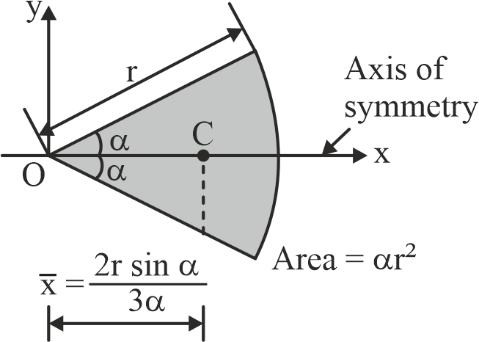
|
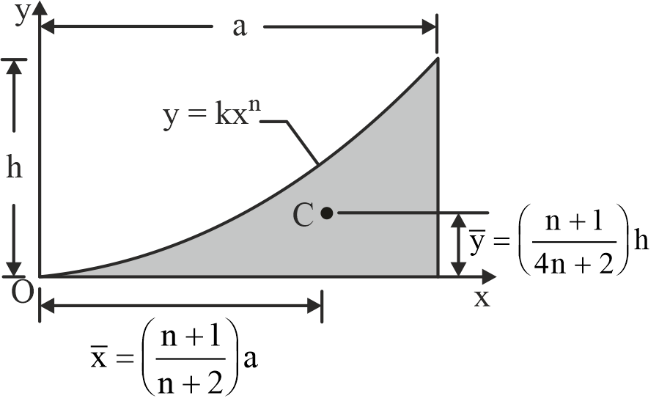
|
Centroid Calculation of Composite Area
Follow these steps to determine the moment of inertia of a composite shape:- Step 1: Divide the composite area into simpler known geometric areas.
- Step 2: Determine the area and the centroid coordinates for each basic geometric area from the origin.
-
Step 3:
Substitute the values into the equation and compute the centroid coordinates of the composite area.
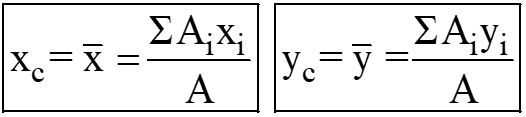
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App