Curvilinear Motion and Its Types

Curvilinear Motion: In the world of engineering, it's essential to understand how things move. Sometimes, objects don't travel in a straight line; instead, they follow curved paths. This kind of motion is called curvilinear motion. Curvilinear motion is a crucial topic as it forms the foundation for understanding more complex motion and dynamic systems.

The kinematics of particles refers to the study of the motion of particles, excluding the forces causing the motion. A particle signifies an entity with mass but insignificant dimensions. In simple words, if an object's shape and size don't impact its motion analysis, it's treated as a particle. By asserting that bodies are treated as particles, we're focusing only on their motion as an entire unit; any spinning around their center of mass is ignored.

Motion and its Types

A body is considered to be in motion when it undergoes a change in position relative to a reference point. The understanding of motion is crucial in designing, analysing, and predicting the behaviour of mechanical systems.

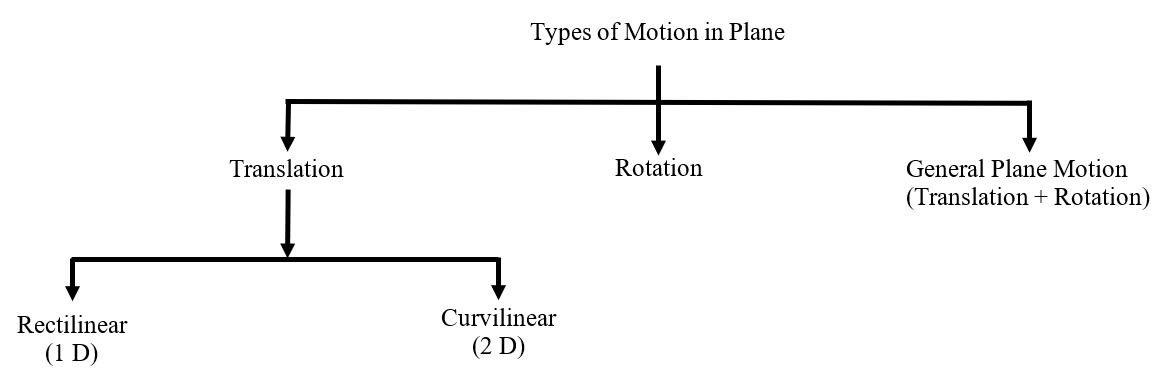
Based on the classification provided, it is clear that curvilinear motion falls under the category of translational motion. Consequently, our focus in this discussion will be exclusively on translational motion.

Translational Motion

Translational motion involves all particles of an object moving along parallel paths, ensuring equal displacement for each particle. This allows treating the object as a single particle for analysis. Based on the characteristics of the trajectory, this motion can be categorized into two distinct types: rectilinear motion and curvilinear motion.

Curvilinear Motion

Curvilinear motion refers to the motion of a particle along a curved path. Unlike rectilinear motion, where an object moves in a straight line, curvilinear motion involves a particle following a trajectory that can be represented by a curve.

• In curvilinear motion, the direction of motion changes continuously as the particle moves. Because the direction of velocity is continuously changing in curvilinear motion, it results in acceleration. This means that all forms of curvilinear motion can be considered as accelerated motion.
• In curvilinear motion, unlike rectilinear motion, the direction of acceleration is not aligned with the direction of motion.
• This type of motion often described in two or three dimensions.
• Position, velocity, and acceleration equations become more complex in this case.

Motion Variables in Curvilinear Motion

In rectilinear motion, all motion variables share the same direction as the path of motion. However, in curved motion, the direction of motion changes continuously. To effectively analyze such motion, we often decompose these motion variables into components, which can be either rectangular components or normal and tangential components.

Rectangular Components of Motion Variables

• Position: The position vector ( ) of a particle defines its location in space relative to a chosen reference point.

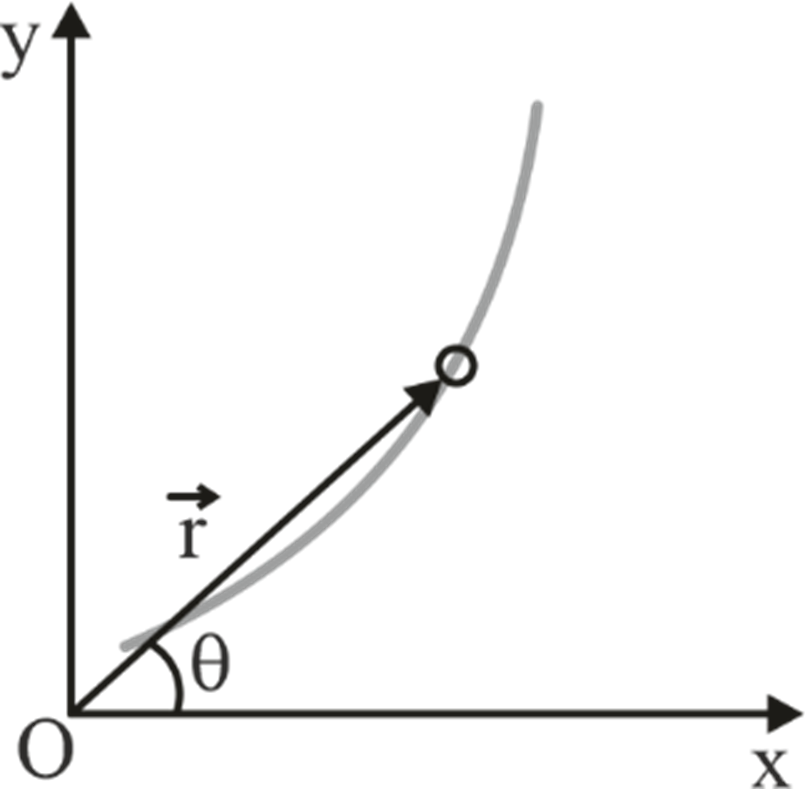
The position vector for a particle (in plane) is given as follows:

In three dimensions:

Where x, y, and z represent the particle's coordinates at any given time. The magnitude and direction of position vector is calculated as;

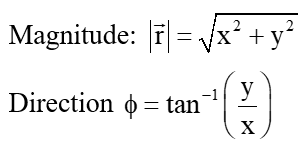
• Displacement: The displacement (∆r) of a particle in curvilinear motion can be calculated using the vector equation.

• Velocity: The particle's velocity in curvilinear motion is always tangent to the curved path at all instants. The velocity of a particle in curvilinear motion is the rate of change of displacement with respect to time.

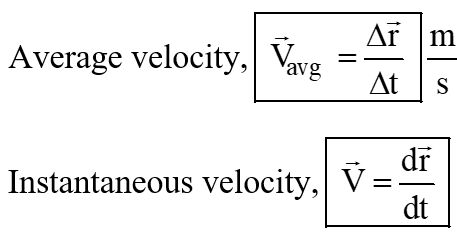
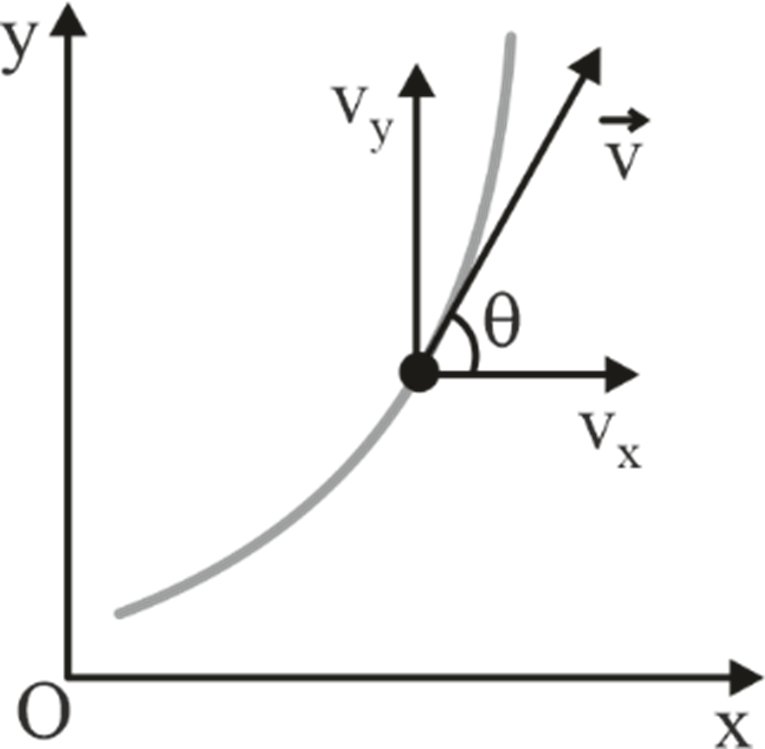
The velocity vector for a particle (in plane) is given as follows;

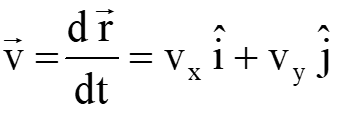
Magnitude and the direction of the velocity vector;

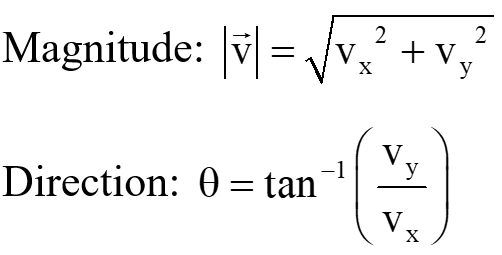
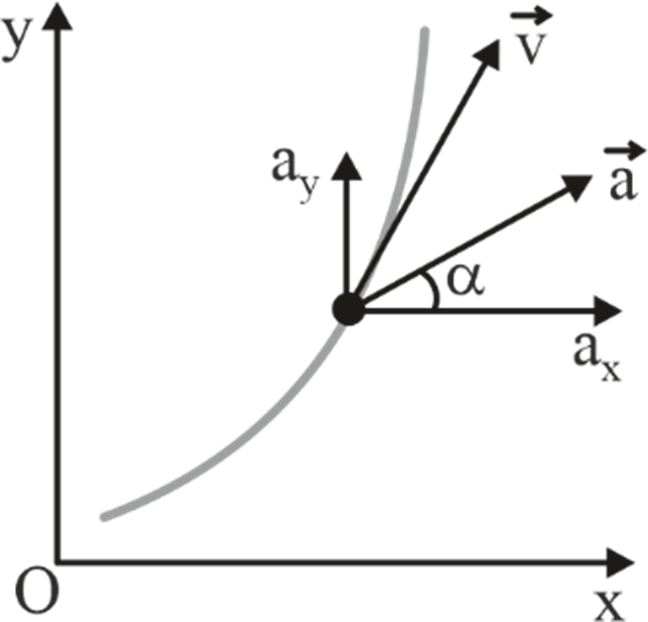
• Acceleration: The object's acceleration aligns with the direction of the change in velocity.

The acceleration vector for a particle (in plane) is given as follows;

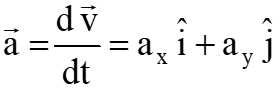
Magnitude and the direction of the acceleration vector;

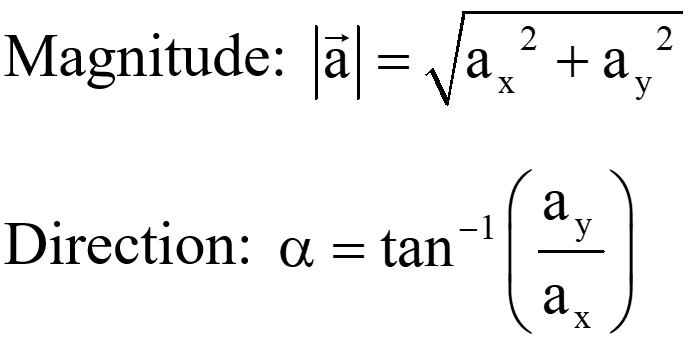
Normal & Tangential Components of Motion Variables

To effectively analyze such motion, the motion variable can also be broken down into normal and tangential components. The normal component of motion refers to the part of an object's motion that is perpendicular or "normal" to a specific reference direction or surface. The tangential component of motion, on the other hand, refers to the part of an object's motion that is parallel or tangent to the direction of its motion.

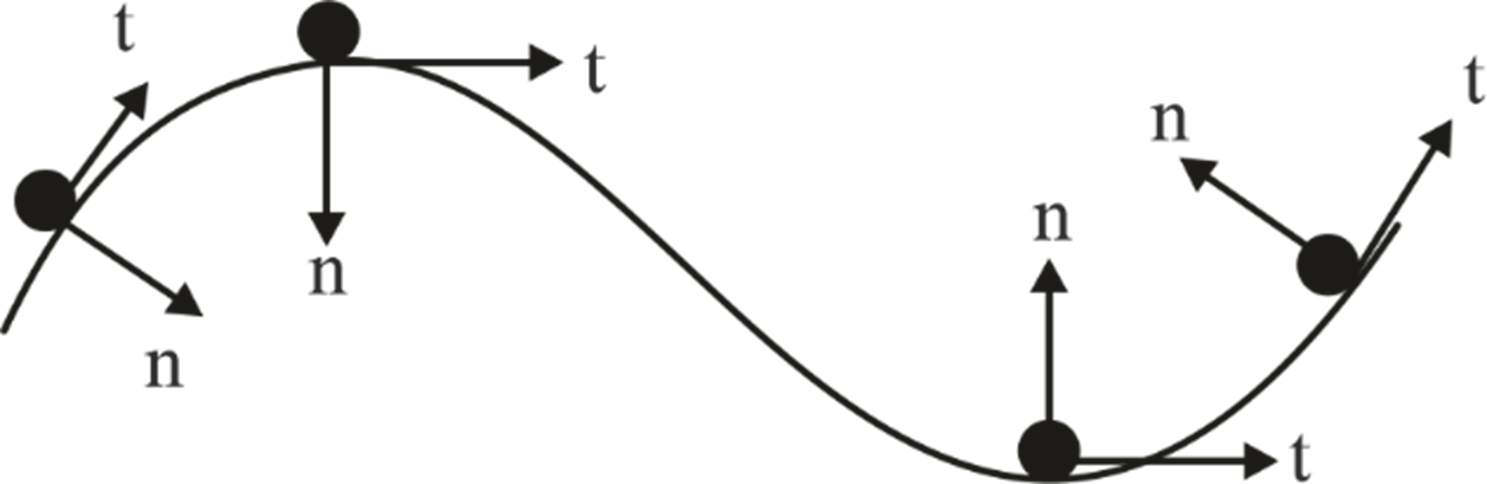
• Velocity in curvilinear motion is always tangent to the curved path.
• Tangential acceleration is the component of acceleration in the tangential direction of the curved path that occurs due to a change in magnitude of velocity.

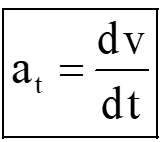
Tangential and normal component of the total acceleration is shown below.

• Normal acceleration is the acceleration directed towards the center of curvature in a curved path, arising from the instantaneous change in velocity direction.

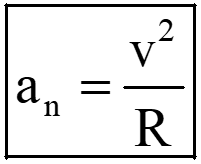
Where R is the radius of the curvature.

Note: Normal acceleration remains nonzero as long as an object is in curvilinear motion.

• Magnitude of total acceleration can be calculated from the relation;
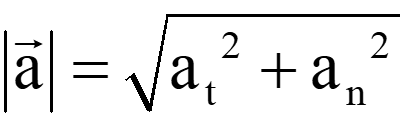
• Direction of total acceleration from the tangential direction can be calculated from the relation;

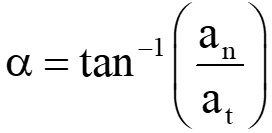
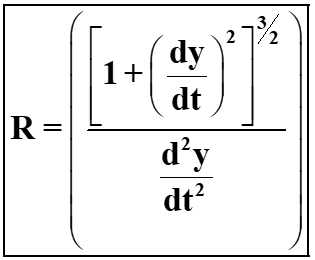
Radius of curvature of Path