

The Area of Hexagon Formula refers to the region enclosed by its six sides. A hexagon is a polygon characterized by six angles and six sides. The term "hexagon" originates from the Greek words 'Hexa,' signifying 'six,' and 'gonía,' signifying 'corner.' In this lesson, we will delve into the concept of hexagonal area, explore the formula for calculating the area of a hexagon, and demonstrate how to determine the area for both regular and irregular hexagons.
What is the Area of a Hexagon?
The hexagon's area refers to the space enclosed by its six sides. A hexagon is a flat geometric shape characterized by six sides, six angles, nine diagonals, and the total measure of its interior angles amounts to 720 degrees.Area of Hexagon a Formula
For a regular hexagon, the area can be calculated using the formula (3√3 s 2 )/2, where 's' represents the length of all its equal sides. This formula allows you to find the area when you know the length of a side of the hexagon.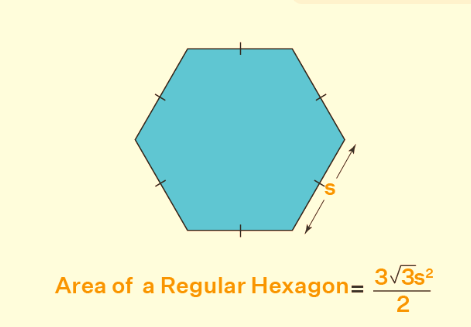
How to Find the Area of a Hexagon?
As discussed in the preceding section, the area of a hexagon can be determined when the length of one of its sides is known. This calculation employs the formula for the area of a regular hexagon, which is given by: Area of a regular hexagon = (3√3 s 2 )/2. To find the area of a hexagon, you can follow these steps: Step 1: Identify the length of one side of the regular hexagon. Step 2: Utilize the formula for the area of a regular hexagon, Area of hexagon = (3√3 s 2 )/2, where 's' represents the side length. Step 3: Express the final result in square units.Also Check - 2cosacosb Formula
Area of Hexagon with Apothem
To determine the area of a regular hexagon, you can use the side length and apothem measurements. The apothem is a line segment drawn from the center of the hexagon to a side, perpendicular to that side. Below, you'll find the formula for calculating the area of a regular hexagon when the apothem is known: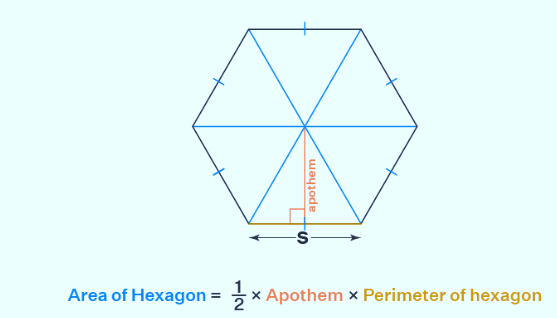
Download PDF Area of Hexagon Formula
Area of a Hexagon with Apothem The formula for this scenario is: Area of hexagon = (1/2) × apothem × Perimeter of hexagon, or, Area of hexagon = (1/2) × a × P = (1/2) × a × 6 × s = 3as, Here's the breakdown: 'a' represents the length of the apothem. 'P' is the perimeter of the hexagon. 's' stands for the length of the hexagon's side. Let's illustrate this with an example.Also Check - Absolute Value Formula
Example: Determine the area of a hexagon with an apothem measuring 12 units and a side length of 8√3 units. Solution: To find the hexagon's area, you can utilize the formula: Area of hexagon = (1/2) × apothem × Perimeter of hexagon. Given that the apothem is 12 units and the perimeter of the hexagon is 6 × 8√3 units = 48√3 units, you can substitute these values into the formula: Area of hexagon = (1/2) × 12 × 48√3 = 288√3 = 498.8 square units.Area of Irregular Hexagon
There isn't a specific formula to calculate the area of an irregular hexagon. Instead, you can break down an irregular hexagon into various simpler shapes, such as rectangles and triangles. By calculating the areas of these individual shapes and then summing them up, you can determine the total area of the irregular hexagon.Examples on Area of a Hexagon Formula
Example 1: Determine the area of a regular hexagon with a side length of 10 units. Solution: Given that the side length is 10 units, you can calculate the hexagon's area using the formula: Area = (3√3 s^2)/2 = (3 × √3 × 10^2)/2 = 150√3 = 259.8 square units Answer: The area of the hexagon is 259.8 square units. Example 2: Find the side length of a regular hexagon with an area of 600√3 square units. Solution: Given the area as 600√3 square units and the formula for the area of a hexagon as (3√3 s^2)/2, you can calculate the side length: (3√3 s^2)/2 = 600√3 (3√3 s^2) = 600√3 × 2 s^2 = (600√3 × 2)/(3√3) s^2 = 400 s = √400 s = 20 units Answer: The length of the side of the regular hexagon is 20 units. Example 3: Calculate the area of a hexagon with the following values: Apothem length = 16.5 inches Perimeter of hexagon = 19 inches Solution: Given the apothem length as 16.5 inches and the perimeter as 19 inches, you can use the formula for hexagon area with apothem: Area = (1/2) × Apothem × Perimeter = (1/2) × 16.5 × 19 = 313.5/2 = 156.75 square inches Answer: The area of the hexagon is 156.75 square inches.Area of Hexagon Formula FAQs
What is a Hexagon?
A hexagon is a polygon with six sides, six angles, and six vertices (corner points). It is a two-dimensional geometric shape that consists of straight line segments connecting these six sides, creating an enclosed figure. All the angles inside a hexagon add up to 720 degrees.
Define the area of Hexagon.
The area of a hexagon is the measure of the space enclosed by its sides. This area is typically expressed in square units, such as square meters (m²), square centimeters (cm²), square inches (in²), square feet (ft²), and so forth.
Define the formula for area of Hexagon.
The area of a hexagon can be calculated using different formulas depending on the type of hexagon:
Regular Hexagon: For a regular hexagon (where all sides and angles are equal), you can use this formula:
Area = (3√3 * s^2) / 2
Where:
"s" is the length of one side of the regular hexagon.
Give some examples of Hexagon shape.
Hexagons can be observed in various natural and human-made objects, including beehives, snowflakes, and numerous artistic and design patterns.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.











