2cosacosb Formula: Derivation, Application, Solved Examples

2cosacosb Formula is one of the product-to-sum formulas in trigonometry, which is used to convert a product of trigonometric functions into a sum of trigonometric functions. Trigonometry is the mathematical field that explores the relationships between angles, heights, and lengths of right triangles. In trigonometry, the ratios of the sides of a right triangle are referred to as trigonometric ratios. There are six main trigonometric ratios: sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). Each of these ratios has its own unique formula and properties.

The 2cosacosb formula specifically involves the cosine (cos) function and its relationship with angles. This formula allows you to express a product of two cosine functions in terms of a sum of trigonometric functions. It is often used in trigonometric identities and equations to simplify expressions or solve trigonometric equations.

To understand this formula in detail, you would typically apply it in the context of a specific trigonometric problem or identity. Depending on the problem at hand, you might need to manipulate trigonometric expressions using this formula to simplify or solve equations involving cosine functions.

What is 2 cos a cos b?

The formula 2cos(A)cos(B) can be expressed as 2 cos A cos B = cos (A + B) + cos (A – B), effectively transforming the product of two cosine functions into the sum of two other cosine functions. This formula is particularly useful in trigonometry for simplifying expressions or solving equations involving cosine functions. For instance:

When applied to 2 cos (2x) cos (2y), it becomes cos (2x + 2y) + cos (2x - 2y).

Similarly, for 2 cos (x/2) cos (y/2), it transforms into cos (x/2 + y/2) + cos (x/2 - y/2).

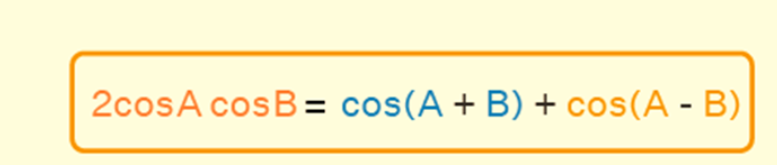
Also Check - Rational Number Formula

2cosacosb Formula Derivation

Let's explore the derivation of this formula. Utilizing the trigonometric sum and difference formulas, we have:

cos (A + B) = cos A cos B – sin A sin B ….. (1)

cos (A – B) = cos A cos B + sin A sin B ….. (2)

When we add equations (1) and (2), the terms involving sin A sin B cancel out in both equations, yielding:

cos (A + B) + cos (A – B) = 2 cos A cos B

Therefore, we can express the 2 cos A cos B formula as:

2 cos A cos B = cos (A + B) + cos (A – B)

This formula allows us to calculate the product of the cosine values of two angles A and B in a right triangle.

Also Check - Linear Equation Formula

Example 1: Find the expression for 8 cos y cos 2y using the sum function.

Solution: To express 8 cos y cos 2y in terms of the sum function, we can start by factoring out 4:

8 cos y cos 2y = 4 [2 cos y cos 2y]

Now, we can apply the formula for 2cosAcosB:

2 cos A cos B = cos (A + B) + cos (A – B)

Using this formula:

4[cos (y + 2y) + cos (y – 2y)]

Simplifying:

4[cos 3y + cos (-y)]

Since cosine is an even function (cos (-x) = cos x), this becomes:

4 [cos 3y + cos y]

Answer: Therefore, 8 cos y cos 2y can be expressed in terms of the sum function as 4 [cos 3y + cos y].

Also Check - Quadrilaterals Formula

Example 2: Express 20 cos x cos 4x as a sum of trigonometric functions.

Solution: To represent 20 cos x cos 4x as a sum, we can begin by factoring out 10:

20 cos x cos 4x = 10 [2 cos x cos 4x]

Now, applying the 2cosAcosB formula:

2 cos A cos B = cos (A + B) + cos (A – B)

Using this formula:

10 [cos (x + 4x) + cos (x – 4x)]

Simplifying:

10 [cos 5x + cos (-3x)]

Since cosine is an even function (cos (-x) = cos x), this simplifies to:

10 [cos 5x + cos 3x]

Answer: Hence, 20 cos x cos 4x can be expressed as the sum of trigonometric functions: 10 [cos 5x + cos 3x].

Example 3: Determine the value of the integral ∫ 2 cos x cos 3x dx.

Solution:

We can utilize the 2cosAcosB formula to simplify the expression:

2 cos A cos B = cos (A + B) + cos (A – B)

In this case, applying the formula:

2 cos x cos 3x = cos (x + 3x) + cos (x - 3x)

= cos 4x + cos (-2x)

= cos 4x + cos 2x (as cos(-θ) = cos θ)

Now, the given integral can be expressed as:

∫ 2 cos x cos 3x dx = ∫ (cos 4x + cos 2x) dx

To integrate, we can apply the substitution method:

= (1/4) sin 4x + (1/2) sin 2x + C

Answer: Therefore, the value of ∫ 2 cos x cos 3x dx is (1/4) sin 4x + (1/2) sin 2x + C.

Example 4: Represent the expression 3 cos 5x cos 7x using the sum of trigonometric functions.

To express 3 cos 5x cos 7x in terms of the sum function, you can use the product-to-sum trigonometric identity:

cos(A)cos(B) = 0.5[cos(A + B) + cos(A - B)]

In this case, A = 5x and B = 7x:

3 cos 5x cos 7x = 3 * 0.5 [cos(5x + 7x) + cos(5x - 7x)]

Now, simplify the expression:

3 cos 5x cos 7x = 1.5 [cos(12x) + cos(-2x)]

Since cosine is an even function (cos(-θ) = cos(θ)), the expression becomes:

3 cos 5x cos 7x = 1.5 [cos(12x) + cos(2x)]

So, 3 cos 5x cos 7x can be expressed in terms of the sum function as:

1.5 [cos(12x) + cos(2x)]

Example 5: Demonstrate the trigonometric identity: cos 2x cos (3x/2) – cos 3x cos (5x/2) = sin x sin (9x/2).

To prove the trigonometric identity cos 2x cos (3x/2) - cos 3x cos (5x/2) = sin x sin (9x/2), you can use trigonometric identities and simplify the expression step by step:

Start with the left-hand side (LHS):

LHS = cos 2x cos (3x/2) - cos 3x cos (5x/2)

Now, apply the product-to-sum identity for cosine:

cos A cos B = 0.5[cos(A + B) + cos(A - B)]

For the first term:

cos 2x cos (3x/2) = 0.5[cos(2x + 3x/2) + cos(2x - 3x/2)]

= 0.5[cos(4x/2 + 3x/2) + cos(4x/2 - 3x/2)]

= 0.5[cos(7x/2) + cos(x/2)]

For the second term:

cos 3x cos (5x/2) = 0.5[cos(3x + 5x/2) + cos(3x - 5x/2)]

= 0.5[cos(6x/2 + 5x/2) + cos(6x/2 - 5x/2)]

= 0.5[cos(11x/2) + cos(x/2)]

Now, substitute these results back into the LHS:

LHS = (0.5[cos(7x/2) + cos(x/2)]) - (0.5[cos(11x/2) + cos(x/2)])

Next, subtract the second term from the first term:

LHS = 0.5[cos(7x/2) + cos(x/2) - cos(11x/2) - cos(x/2)]

Now, notice that the cos(x/2) terms cancel out:

LHS = 0.5[cos(7x/2) - cos(11x/2)]

Apply the sum-to-product identity for cosine:

cos A - cos B = -2sin((A + B)/2)sin((A - B)/2)

In this case, A = 11x/2 and B = 7x/2:

LHS = -2 * 0.5[sin((11x/2 + 7x/2)/2)sin((11x/2 - 7x/2)/2)]

LHS = -sin(9x/2)sin(2x/2)

LHS = -sin(9x/2)sin(x)

Now, the LHS is equal to:

LHS = -sin(9x/2)sin(x)

So, the identity is proven:

LHS = -sin(9x/2)sin(x) = sin(x)sin(9x/2) = RHS

The left-hand side (LHS) is equal to the right-hand side (RHS), which means the trigonometric identity cos 2x cos (3x/2) - cos 3x cos (5x/2) = sin x sin (9x/2) is proven.

Example 6 : Find the value of the integral of 2 cos 4x cos (5x/2) dx?

Solution : To find the integral of 2 cos 4x cos (5x/2) dx, you can use the product-to-sum trigonometric identity:

cos(A)cos(B) = 0.5[cos(A + B) + cos(A - B)]

In this case, A = 4x and B = 5x/2:

2 cos 4x cos (5x/2) = 2 * 0.5 [cos(4x + 5x/2) + cos(4x - 5x/2)]

Now, simplify the expression:

2 cos 4x cos (5x/2) = cos(13x/2) + cos(3x/2)

To find the integral of this expression with respect to x, you can integrate each term separately:

∫ [cos(13x/2) + cos(3x/2)] dx

Integrate each term:

∫ cos(13x/2) dx + ∫ cos(3x/2) dx

Now, integrate using the power rule:

For ∫ cos(13x/2) dx, you can let u = 13x/2, and then du = (13/2)dx. So, the integral becomes:

(2/13) ∫ cos(u) du

Integrate cos(u) with respect to u:

(2/13) * sin(u)

Now, reverse the substitution:

(2/13) * sin(13x/2)

For ∫ cos(3x/2) dx, you can let v = 3x/2, and then dv = (3/2)dx. So, the integral becomes:

(2/3) ∫ cos(v) dv

Integrate cos(v) with respect to v:

(2/3) * sin(v)

Now, reverse the substitution:

(2/3) * sin(3x/2)

Now, combine both results:

(2/13) * sin(13x/2) + (2/3) * sin(3x/2) + C

Where C is the constant of integration.

So, the value of the integral of 2 cos 4x cos (5x/2) dx is:

(2/13) * sin(13x/2) + (2/3) * sin(3x/2) + C