Important Questions for Class 7 Maths Chapter 6 The Triangle and Its Properties
Neha Tanna20 Dec, 2024
Share
Important Questions for Class 7 Maths Chapter 6: Chapter 6, The Triangle and Its Properties, in Class 7 Maths, introduces the fundamental aspects of triangles. Key topics include the classification of triangles (based on sides and angles), the triangle inequality theorem, and the properties of a triangle, such as the angle sum property. Students also learn about medians, altitudes, and the Pythagoras theorem.
Important questions typically involve proving the triangle inequality, calculating unknown angles using the angle sum property, and solving problems related to medians and altitudes. These questions enhance problem-solving skills and deepen understanding of geometric principles, essential for higher-level mathematics.Important Questions for Class 7 Maths Chapter 6 Overview
Chapter 6, The Triangle and Its Properties, is a crucial part of Class 7 Maths, laying the foundation for advanced geometry. Understanding triangles' properties, such as the angle sum property, triangle inequality, medians, altitudes, and Pythagoras theorem, is vital for solving complex problems. Important questions from this chapter help students apply these concepts practically, improving logical thinking and spatial understanding. These include proving the triangle inequality, finding unknown angles, and solving problems related to medians and altitudes. Mastering these concepts is essential, as they form the basis for higher studies in mathematics, engineering, and various competitive exams.Important Questions for Class 7 Maths Chapter 6 PDF
Chapter 6, The Triangle and Its Properties, focuses on essential geometric concepts such as triangle inequality, angle sum property, medians, altitudes, and the Pythagoras theorem. These are fundamental for understanding higher-level geometry. Below, we have provided a PDF containing important questions from this chapter to enhance your preparation effectively.Important Questions for Class 7 Maths Chapter 6 PDF
Important Questions for Class 7 Maths Chapter 6 The Triangle and Its Properties
Below is the Important Questions for Class 7 Maths Chapter 6 The Triangle and Its Properties -Question 1.
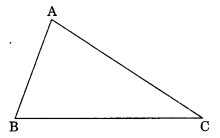
In ∆ABC, write the following:
(a) Angle opposite to side BC.
(b) The side opposite to ∠ABC.
(c) Vertex opposite to side AC.
Solution:
(a) In ∆ABC, Angle opposite to BC is ∠BAC
(b) Side opposite to ∠ABC is AC
(c) Vertex opposite to side AC is B
Question 2.
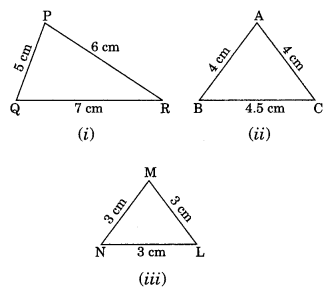
Classify the following triangle on the bases of sides
Solution:
(i) PQ = 5 cm, PR = 6 cm and QR = 7 cm
PQ ≠ PR ≠ QR
Thus, ∆PQR is a scalene triangle.
(ii) AB = 4 cm, AC = 4 cm
AB = AC
Thus, ∆ABC is an isosceles triangle.
(iii) MN = 3 cm, ML = 3 cm and NL = 3 cm
MN = ML = NL
Thus, ∆MNL is an equilateral triangle.
Question 3.
In the given figure, name the median and the altitude. Here E is the midpoint of BC.
Solution In ∆ABC, we have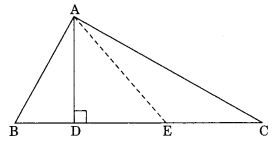
AD is the altitude.
AE is the median.
Question 4.
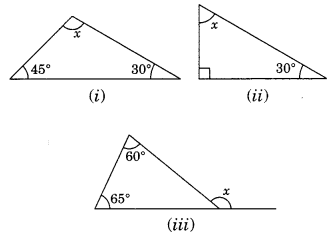
In the given diagrams, find the value of x in each case.
Solution:
(i) x + 45° + 30° = 180° (Angle sum property of a triangle)
⇒ x + 75° – 180°
⇒ x = 180° – 75°
x = 105°
(ii) Here, the given triangle is right angled triangle.
x + 30° = 90°
⇒ x = 90° – 30° = 60°
(iii) x = 60° + 65° (Exterior angle of a triangle is equal to the sum of interior opposite angles)
⇒ x = 125°
Question 5.
Which of the following cannot be the sides of a triangle?
(i) 4.5 cm, 3.5 cm, 6.4 cm
(ii) 2.5 cm, 3.5 cm, 6.0 cm
(iii) 2.5 cm, 4.2 cm, 8 cm
Solution: (i) Given sides are, 4.5 cm, 3.5 cm, 6.4 cm Sum of any two sides = 4.5 cm + 3.5 cm = 8 cm Since 8 cm > 6.4 cm (Triangle inequality) The given sides form a triangle. (ii) Given sides are 2.5 cm, 3.5 cm, 6.0 cm Sum of any two sides = 2.5 cm + 3.5 cm = 6.0 cm Since 6.0 cm = 6.0 cm The given sides do not form a triangle. (iii) 2.5 cm, 4.2 cm, 8 cm Sum of any two sides = 2.5 cm + 4.2 cm = 6.7 cm Since 6.7 cm < 8 cm The given sides do not form a triangle.Question 6.
In the given figure, find x.
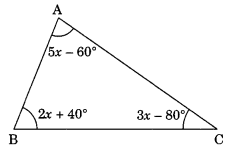Solution:
In ∆ABC, we have
5x – 60° + 2x + 40° + 3x – 80° = 180° (Angle sum property of a triangle)
⇒ 5x + 2x + 3x – 60° + 40° – 80° = 180°
⇒ 10x – 100° = 180°
⇒ 10x = 180° + 100°
⇒ 10x = 280°
⇒ x = 28°
Thus, x = 28°
Question 7.
One of the equal angles of an isosceles triangle is 50°. Find all the angles of this triangle.
Solution: Let the third angle be x°. x + 50° + 50° = 180° ⇒ x° + 100° = 180° ⇒ x° = 180° – 100° = 80° Thus ∠x = 80°Benefits of Using Important Questions for Class 7 Maths Chapter 6
Using Important Questions for Class 7 Maths Chapter 6 - The Triangle and Its Properties offers several benefits:Concept Clarity : Reinforces understanding of key concepts like triangle inequality, angle sum property, medians, and altitudes.
Exam Preparation : Focuses on frequently asked and high-scoring questions.
Practice for Accuracy : Enhances problem-solving skills and boosts speed and accuracy.
Critical Thinking : Develops logical reasoning and analytical skills.
Confidence Building : Strengthens understanding of fundamentals, preparing students for advanced topics and competitive exams.
Time Management : Helps identify important topics, saving time during revision.
Important Questions for Class 7 Maths Chapter 6 FAQs
What is the concept of properties of triangle?
What do triangles have in common?
What is the basic concept of a triangle?
What is the property of triangle based on side?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
