NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3 PDF Download
Get detailed NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3. Understand key concepts and enhance your learning with clear explanations and step-by-step solutions.
Ananya Gupta3 Jan, 2025
Share
NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3: Exercise 1.3 of Chapter 1 Real Numbers in Class 10 Maths focuses on problems related to the division algorithm. This exercise helps students understand how to find the quotient and remainder when one number is divided by another, which is an important concept for working with real numbers.
The solutions provide detailed steps for applying the division algorithm to different pairs of numbers and help in understanding how to express the relationship between two numbers using division, quotient, and remainder. Solving these problems enhances students understanding of number theory and improves their ability to solve complex mathematical problems involving division. The solutions are a useful guide for exam preparation, ensuring a deeper comprehension of the topic.NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3 Overview
NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3 PDF
The NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3 provide clear and detailed explanations on the Division Algorithm and its applications. These solutions help in understanding how to express the relationship between two numbers in terms of quotient and remainder. To access the PDF of the solutions click on the link below.NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3 PDF
NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3
Here are the NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3:1. Prove that √ 5 is irrational.
Solutions: Let us assume that √ 5 is a rational number.
i.e., √ 5 = x/y (where, x and y are co-primes) y √ 5= x Squaring both sides, we get (y √ 5) 2 = x 2 ⇒5y 2 = x 2 ……………………………….. (1) Thus, x 2 is divisible by 5, so x is also divisible by 5. Let us say, x = 5k, for some value of k, and substituting the value of x in equation (1), we get 5y 2 = (5k) 2 ⇒y 2 = 5k 2 is divisible by 5, it means y is divisible by 5. Clearly, x and y are not co-primes. Thus, our assumption about √ 5 is rational is incorrect. Hence, √ 5 is an irrational number.2. Prove that 3 + 2√5 + is irrational.
Solutions: Let us assume 3 + 2 √ 5 is rational.
Then, we can find co-prime x and y (y ≠ 0) such that 3 + 2√5 = x/y Rearranging, we get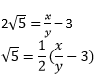
x and y are integers, thus
is a rational number.
Therefore,
√
5 is also a rational number. But this contradicts the fact that
√
5 is irrational.
So, we conclude that 3 + 2
√
5 is irrational.
3. Prove that the following are irrational.
(i) 1/√2
(ii) 7√5
(iii) 6 + √ 2
Solutions:
(i) 1/ √ 2
Let us assume 1/√2 is rational. Then, we can find co-prime x and y (y ≠ 0) such that 1/√2 = x/y Rearranging, we get √2 = y/x x and y are integers; thus, √2 is a rational number, which contradicts the fact that √2 is irrational. Hence, we can conclude that 1/√2 is irrational.(ii) 7 √ 5
Let us assume 7√5 is a rational number. Then, we can find co-prime a and b (b ≠ 0) such that 7√5 = x/y Rearranging, we get √5 = x/7y x and y are integers; thus, √5 is a rational number, which contradicts the fact that √5 is irrational. Hence, we can conclude that 7√5 is irrational.(iii) 6 + √ 2
Let us assume 6 +√2 is a rational number. Then, we can find co-primes x and y (y ≠ 0) such that 6 +√2 = x/y Rearranging, we get √2 = (x/y) – x and y are integers; thus, (x/y) – 6 is a rational number and therefore, √2 is rational. This contradicts the fact that √2 is an irrational number. Hence, we can conclude that 6 +√2 is irrational.Benefits of Solving NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3
- Understanding the Division Algorithm : This exercise helps students grasp the Division Algorithm which is a fundamental concept in number theory. By solving the problems, students learn how to express the relationship between two integers in terms of quotient and remainder.
- Improved Problem-Solving Skills : The problems in Exercise 1.3 require students to apply the Division Algorithm which enhances their ability to solve real-life mathematical problems involving division, quotients, and remainders.
- Strong Foundation for Future Concepts : The concepts learned in this exercise are crucial for understanding more advanced topics in mathematics, such as factorization, LCM, HCF, and algebraic manipulations.
- Conceptual Clarity : The solutions provide a clear, step-by-step breakdown of the division process, helping students understand how to approach division problems systematically.
- Exam Readiness : By solving problems from Exercise 1.3 students prepare themselves for board exams, as these types of problems are often included in Class 10 Maths exams. Regular practice helps improve accuracy and speed.
- Increased Confidence : Consistent practice using the NCERT solutions boosts students' confidence and strengthens their overall mathematical skills, making them more capable of tackling complex problems.
- Better Grasp of Real Numbers : Exercise 1.3 focuses on the division of real numbers which is important for mastering the concept of real numbers and understanding their properties more deeply.
NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.3 FAQs
Can a real number be negative?
Yes, real numbers can be both positive and negative. For example, -2, -0.5, and -π are all negative real numbers.
Are integers considered real numbers?
Yes, integers are a subset of real numbers. All integers, such as -3, 0, and 7, are real numbers because they can be represented on the number line.
What is the Fundamental Theorem of Arithmetic?
The Fundamental Theorem of Arithmetic states that every integer greater than 1 is either a prime number or can be uniquely factorized as a product of primes, with the order of factors not affecting the result.
Is zero a real number?
Yes, zero is a real number.
Are fractions real numbers?
Yes, fractions like 1/2, -3/4, and 7/8 are real numbers. Any number that can be expressed as the ratio of two integers is a rational number and, hence, a real number.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.