
Polygon Formula: A polygon is a two-dimensional geometric shape that is enclosed by three or more straight line segments. It's important to note that a polygon must have a minimum of three sides to qualify as such. At the vertices of these line segments, they intersect with one another. Now, let's delve into various types of polygons and explore the mathematical formulas associated with them.
What is Polygon Formula?
Here are some essential formulas associated with regular polygons:
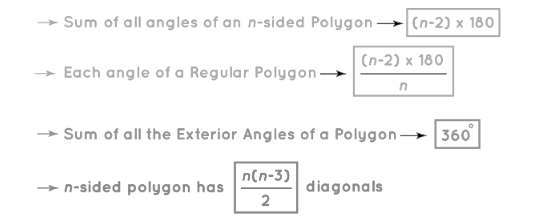
Formula 1: The sum of interior angles in a regular 'n'-sided polygon is given by 180°(n-2).
Formula 2: The number of diagonals in an 'n-sided' polygon can be calculated using the formula [n(n-3)]/2.
Formula 3: The measure of each interior angle in a regular 'n'-sided polygon is [(n-2)180°]/n.
Formula 4: The measure of exterior angles in a regular 'n'-sided polygon is 360°/n.
Formula 5: To find the area of a regular polygon, you can use the formula (number of sides × length of one side × apothem)/2. The length of the apothem is calculated as l / [2tan(180/n)], where 'l' represents the side length, and 'n' is the number of sides of the regular polygon.
Formula 6: Expressing the area of a regular polygon in terms of its perimeter, you can use the formula Area = (Perimeter × apothem)/2, where the perimeter is determined by multiplying the number of sides by the length of one side.
Types of Polygon
Polygons can be categorized based on the measure of their angles and the lengths of their sides, leading to the following classifications:
Regular Polygon: In a regular polygon, all the interior angles and sides have the same measurement.
Irregular Polygon: An irregular polygon is characterized by interior angles and sides with varying measurements.
Convex Polygon: Convex polygons are those in which all interior angles are less than 180 degrees.
Concave Polygon: Concave polygons are polygons with one or more interior angles that measure greater than 180 degrees.
The shape and name of a polygon are determined by the number of its sides. Hence, examples of polygons include triangles, squares, pentagons, hexagons, and so on. Below is a list of polygons named according to the number of sides they possess.

Properties of Polygon
The sum of the interior angles of any quadrilateral (four-sided polygon) is always equal to 360°.
If a polygon has at least one interior angle measuring greater than 180 degrees, it is classified as a concave polygon. In contrast, polygons with all interior angles less than 180 degrees are convex.
A polygon is considered a simple polygon if it does not self-intersect and has only one continuous boundary. If a polygon has multiple overlapping or intersecting boundaries, it is defined to as a complex polygon.
Polygon Formula Examples
Example 1: Finding the Sum of Interior Angles
Suppose you have a regular pentagon (a polygon with 5 sides) and want to calculate the sum of its interior angles using Formula 1.
n (number of sides) = 5
Sum of interior angles = 180°(5-2) = 180°(3) = 540°
So, the sum of interior angles of a regular pentagon is 540 degrees.
Example 2: Calculating the Number of Diagonals
Let's say you have a hexagon (a polygon with 6 sides) and you want to determine the number of diagonals using Formula 2.
n (number of sides) = 6
Number of diagonals = [6(6-3)]/2 = 18/2 = 9 diagonals
So, a hexagon has 9 diagonals.
Example 3: Finding the Measure of Each Interior Angle
Suppose you have an octagon (a polygon with 8 sides) and you want to find the measure of each interior angle using Formula 3.
n (number of sides) = 8
Each interior angle = [(8-2)180°]/8 = (6/8)180° = 135°
The measure of each interior angle in a regular octagon is 135 degrees.
Example 4: Calculating the Measure of Exterior Angles
Let's say you have a decagon (a polygon with 10 sides) and you want to find the measure of each exterior angle using Formula 4.
n (number of sides) = 10
Each exterior angle = 360°/10 = 36°
The measure of each exterior angle in a regular decagon is 36 degrees.
Example 5: Finding the Area of a Regular Polygon
Suppose you have a regular hexagon with a side length of 8 units, and you want to calculate its area using Formula 5:
n (number of sides) = 6
Length of one side (l) = 8 units
Calculate the apothem: apothem = 8 / [2tan(180/6)] = 4√3 units
Area = (6 * 8 * 4√3) / 2 = 96√3 square units
The area of the regular hexagon is 96√3 square units.
| Related Links | |
| Coin Toss Probability Formula | Probability |
| Probability formula | Consecutive Integers Formula |
Polygon Formula FAQs
Q1. What is the sum of the interior angles of a polygon?
Q2. How do you find the number of diagonals in a polygon?
Q3. How do I find the measure of each interior angle in a regular polygon?
Q4. How can I calculate the measure of exterior angles in a regular polygon?
Q5. How do I determine the area of a regular polygon?










