RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.4 Pair of Linear Equations in Two Variables
Neha Tanna4 Nov, 2024
Share
RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.4: Exercise 3.4 of RD Sharma's Class 10 Maths focuses on solving pairs of linear equations in two variables using various methods, including substitution, elimination, and graphical representation. Students learn to set up equations based on given word problems and solve them to find the values of the variables.
This exercise emphasizes understanding the relationship between the equations, identifying consistent, inconsistent, and dependent systems, and interpreting the solutions in real-world contexts. By practicing these problems, students enhance their problem-solving skills and gain confidence in handling linear equations effectively.RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.4 Overview
RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.4 PDF
In this section, we present the RD Sharma Solutions for Class 10 Maths, Chapter 3, Exercise 3.4, which focuses on pairs of linear equations in two variables. This exercise equips students with essential techniques for solving linear equations using methods like substitution and elimination. To facilitate your understanding and practice, we have provided a PDF containing detailed solutions and explanations. Access the PDF below to enhance your grasp of this important mathematical concept and improve your problem-solving skills.RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.4 PDF
RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.4 Pair of Linear Equations in Two Variables
Below is the RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.4 Pair of Linear Equations in Two Variables -Solve each of the following systems of equations by the method of cross-multiplication:
1. x + 2y + 1 = 0
2x – 3y – 12 = 0
Solution:
The given systems of equations arex + 2y + 1 = 0
2x – 3y – 12 = 0
For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = 3 and y = -2.
2. 3x + 2y + 25 = 0
2x + y + 10 = 0
Solution:
The given system of equations is3x + 2y + 25 = 0
2x + y + 10 = 0
For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = 5 and y = -20.
3. 2x + y = 35, 3x + 4y = 65
Solution:
The given system of equations can be written as2x + y – 35 = 0
3x + 4y – 65 = 0
For cross-multiplication, we use,
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = 15 and y = 5.
4. 2x – y = 6, x – y = 2
Solution:
The given system of equations can be written as2x – y – 6 = 0
x – y – 2 = 0
For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = 4 and y = 2.
5. (x + y)/ xy = 2
(x – y)/ xy = 6
Solution:
The given system of equations is (x + y)/ xy = 2 ⇒ 1/y + 1/x = 2…….. (i) (x – y)/ xy = 6 ⇒ 1/y – 1/x = 6……… (ii) Let 1/x = u and 1/y = v, so the equation becomes u + y = 2….. (iii) u – y = 6……(iv)For cross-multiplication, we use
Comparing the above two equations (iii) & (iv) with the general form, we get
Hence, the solution for the given system of equations is x = -1/2 and y = 1/4.
6. ax + by = a-b
bx – ay = a+b
Solution:
The given system of equations can be written asax + by – (a-b) = 0
bx – ay – (a+b) = 0
For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = 1 and y = -1.
7. x + ay = b
ax + by = c
Solution:
The given system of equations can be written as x + ay – b = 0 ax + by – c = 0For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = (b
2
+ ac)/(a
2
+ b
2
).
and y = (-c
2
+ ab)/(a
2
+ b
2
).
8. ax + by = a 2
bx + ay = b 2
Solution:
The given system of equations can be written asax + by – (a 2 ) = 0
bx + ay – (b 2 ) = 0
For cross-multiplication, we use
Comparing the above two equations with the general form, we get
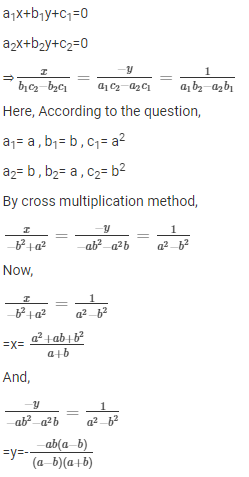Hence, the solution for the given system of equations is x = (a
2
+ ab + b
2
)/(a + b) and y = -ab / (a+ b).
9. 5/(x + y) – 2/(x -y) = -1
15/(x + y) + 7/(x – y) = 10
Solution:
Let’s substitute 1/(x + y) = u and 1/(x – y) = v, so the given equations becomes 5u – 2v = -1 15u + 7v = 10For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = 3 and y = 2.
10. 2/x + 3/y = 13
5/x – 4/y = -2
Solution:
Let 1/x = u and 1/y = v, so the equation becomes 2u + 3y = 13 ⇒ 2u + 3y – 13 = 0 5u – 4y = -2 ⇒ 5u – 4y + 2 = 0For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = 1/2 and y = 1/3.
11. 57/(x + y) + 6/(x – y) = 5
38/(x + y) + 21/(x – y) = 9
Solution:
Let’s substitute 1/(x + y) = u and 1/(x – y) = v, so the given equations becomes 57u + 6v = 5 ⇒ 57u + 6v – 5 = 0 38u + 21v = 9 ⇒ 38u + 21v – 9 = 0For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = 11 and y = 8.
12. xa – yb = 2
ax – by = a 2 -b 2
Solution:
The given system of equations can be written as xa – yb – 2 = 0ax – by – (a 2 -b 2 ) = 0
For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = a and y = b.
13. x/a + y/b = a + b
x/a 2 + y/b 2 = 2
Solution:
The given system of equations can be written as x/a + y/b – (a + b) = 0 x/a 2 + y/b 2 – 2 = 0For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = a
2
and y = b
2
.
14. x/a = y/b
ax + by = a 2 + b 2
Solution:
The given system of equations can be written as x/a – y/b = 0 ax + by – (a 2 + b 2 ) = 0For cross-multiplication, we use
Comparing the above two equations with the general form, we get
Hence, the solution for the given system of equations is x = a and y = b.
Benefits of Solving RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.4
Solving RD Sharma Solutions for Class 10 Maths, Chapter 3, Exercise 3.4 on pairs of linear equations in two variables offers several benefits:Conceptual Understanding : It helps students grasp fundamental concepts of linear equations, enhancing their ability to formulate and solve problems effectively.
Problem-Solving Skills : Engaging with a variety of problems improves analytical and critical thinking skills, essential for tackling complex mathematical challenges.
Application of Methods : Students learn different methods such as substitution, elimination, and graphical representation, equipping them to choose the most effective approach for various problems.
Real-Life Applications : Understanding how to model and solve real-world situations through linear equations fosters practical application of mathematics in everyday life.
Exam Preparation : Regular practice of these exercises aids in exam readiness, boosting confidence and performance in assessments related to linear equations.
Foundation for Advanced Topics : Mastery of this chapter lays a solid foundation for higher-level mathematics, making it easier to grasp advanced concepts in algebra and related fields.
RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.4 FAQs
What is a pair of linear equations in two variables conditions?
What are the conditions for a linear equation?
What is the unique solution in linear equations in two variables?
What are the basic concepts of linear equations in two variables?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
