RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3:
A step-by-step solution to the chapter 10 quadratic equations in the textbook RS Aggarwal class 10 has been developed by the Physics Wallah academic team. The academic team of Physics Wallah created NCERT Solutions, which are used to answer all of the exercise questions in maths class 10.
The RS Aggarwal class 10 solution for chapter-10 Quadratic Equations Exercise-10C is uploaded for reference only; do not copy the solution. Before going through the solution of chapter-10 Quadratic Equations Exercise-10C, one must have a clear understanding of the chapter-10 Quadratic Equations. Therefore, read the theory of Chapter 10 Quadratic Equations, and then try to solve all numerical of exercise-10C.
RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3 Overview
RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3 on Quadratic Equations offers a clear and systematic approach to solving problems related to quadratic equations. This exercise typically focuses on solving equations using various methods such as factoring, completing the square, and applying the quadratic formula.
Each solution is detailed step-by-step, making it easier for students to follow along and understand the process. By working through these problems, students can enhance their problem-solving skills, reinforce their understanding of quadratic equations, and build confidence in their ability to tackle similar questions in exams.
What are Quadratic equations?
A polynomial equation of second degree, or one that has at least one squared term, is referred to as a quadratic. Another name for it is quadratic equations. The quadratic equation has the following generic form:
ax² + bx + c = 0
where a, b, and c are numerical coefficients and x is an unknown variable. In this case, a ≠ 0 since if it does, the equation will no longer be quadratic and will instead become linear, as in the following cases:
bx+c=0
Quadratics Formula
The roots of an equation are found using the method for a quadratic equation. There will be two answers to the equation as the degree of a quadratic is two. Assuming that the quadratic equation is ax² + bx + c = 0, the formula to determine its roots is as follows:
x = [-b±√(b
2
-4ac)]/2a
RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3 PDF
RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3 provides a comprehensive learning experience that equips students with the necessary knowledge and skills to tackle questions confidently. Here we have provided RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3 for the ease of students so that they can prepare better for their upcoming exams –
RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3 PDF
RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3
Below we have provided RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3 for the ease of the students –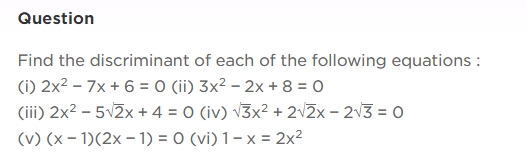
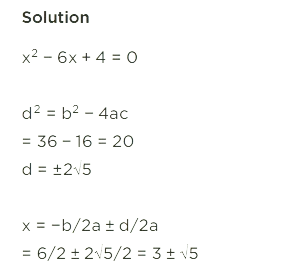
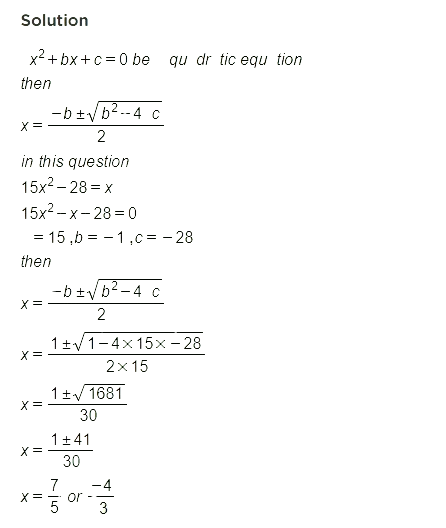
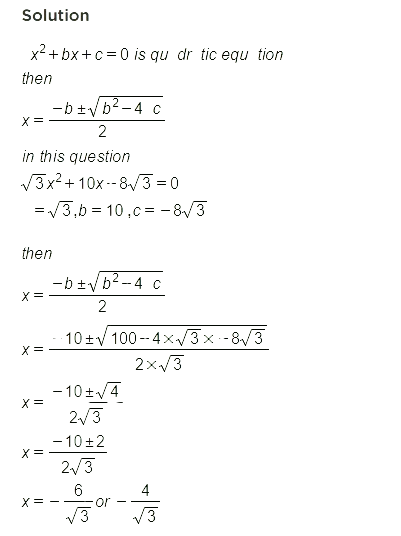
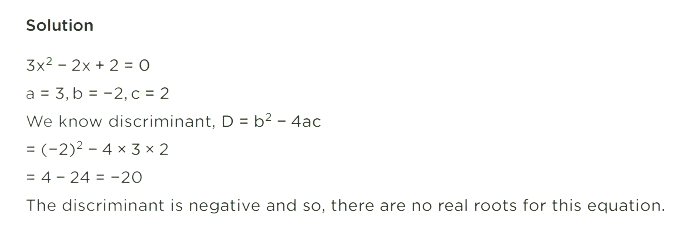
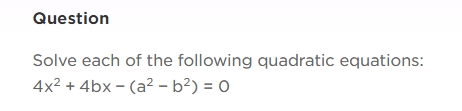
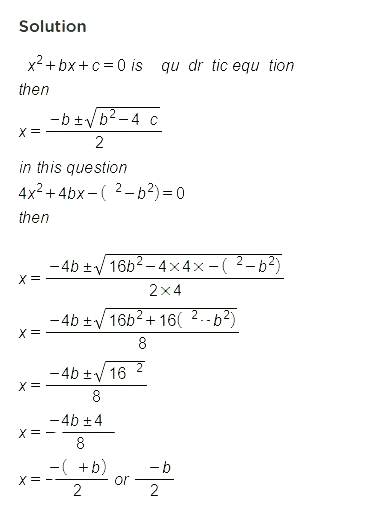
Benefits of RS Aggarwal Solutions for Class 10 Maths Chapter 10 Exercise 10.3
The RS Aggarwal Solutions for Class 10 Maths Chapter 10, Exercise 10.3, which deals with Quadratic Equations, offers several benefits for students. Here’s a detailed look at these advantages:
Comprehensive Understanding
:
Detailed Solutions
: The solutions provide step-by-step explanations, helping students understand the methodology behind solving quadratic equations. This can be particularly useful for grasping complex concepts.
Varied Problems
: The exercise covers a range of problems that help students tackle different types of quadratic equations, enhancing their problem-solving skills.
Exam Preparation
:
Practice and Repetition
: Regular practice with these solutions can improve proficiency and speed in solving quadratic equations, which is crucial for exams.
Clarification of Doubts
: By working through the solutions, students can clear up any misunderstandings about the topic and better prepare for questions in exams.
Concept Reinforcement
:
Application of Concepts
: The solutions reinforce key concepts such as factoring, completing the square, and using the quadratic formula, which are essential for mastering quadratic equations.
Conceptual Links
: The exercise often connects various concepts, helping students see how quadratic equations fit into broader mathematical contexts.
Skill Development
:
Analytical Skills
: Solving these problems enhances analytical thinking and problem-solving abilities.
Error Identification
: By reviewing the solutions, students can learn to identify and correct mistakes in their work, leading to a deeper understanding of the subject.
Confidence Building
:
Improved Performance
: Mastery of the exercise can boost a student's confidence in their ability to handle quadratic equations, leading to improved performance in tests and exams.
Positive Feedback Loop
: Successfully solving problems and seeing detailed solutions can motivate students to continue practicing and improving their skills.
Resourcefulness
:
Exam Strategy
: The structured solutions provide insight into efficient problem-solving techniques that can be applied during exams.
Reference Material
: The solutions serve as a useful reference for revision and self-study, ensuring that students have access to reliable methods and explanations.
