Physics Wallah

RS Aggarwal Solutions for Class 10 Maths Chapter 11 Exercise 11.3 Arithmetic Progressions

In this article we have provided RS Aggarwal Solutions for Class 10 Maths Chapter 11 Exercise 11.3 prepared by our experts to help students to prepare better for their examinations.
authorImageAnanya Gupta18 Jul, 2024
Share

Share

RS Aggarwal Solutions for Class 10 Maths Chapter 11 Exercise 11.3 Arithmetic Progressions

RS Aggarwal Solutions for Class 10 Maths Chapter 11 Exercise 11.3: In Chapter 11 of RS Aggarwal's Class 10 Maths book, which covers Arithmetic Progressions (AP), Exercise 11.3 focuses on determining the number of terms in an AP and finding specific terms based on given information. The exercise involves calculations where students use formulas such as the nth term formula and the formula for the last term of an AP.

These exercises are designed to strengthen understanding of AP concepts and enhance problem-solving skills through practical applications of AP formulas.

RS Aggarwal Solutions for Class 10 Maths Chapter 11 Arithmetic Progressions Exercise 11.3 Overview

The solutions for Chapter 11 Exercise 11.3 of RS Aggarwal's Class 10 Maths have been prepared by subject experts from Physics Wallah. This exercise focuses on Arithmetic Progressions (AP), where students learn to find terms in a sequence and solve problems using basic AP formulas. Each solution is designed to be easy to follow, giving clear steps to help students understand and practice these mathematical concepts effectively.

RS Aggarwal Solutions for Class 10 Maths Chapter 11 Exercise 11.3 PDF

You can access the PDF link for RS Aggarwal Solutions for Class 10 Maths, Chapter 11 Exercise 11.3 below. This PDF provides detailed solutions prepared by subject experts, helping students understand Arithmetic Progressions (AP) and solve problems effectively.

RS Aggarwal Solutions for Class 10 Maths Chapter 11 Exercise 11.3 PDF

RS Aggarwal Solutions for Class 10 Maths Chapter 11 Exercise 11.3

Here we have provided RS Aggarwal Solutions for Class 10 Maths Chapter 11 Arithmetic Progressions Exercise 11.3 for the ease of students so that they can prepare better for their exams.

Q. The sum of the first n terms of an AP is ( 3 n 2 + 6 n ) . Find the nth term and the 15th terms of this AP.

Solution:

Here, first term = 9 Common difference = 7 - 9 = - 2 Sum of first n terms of an AP is Sn = n 2 [2a + (n - 1)d] ∴ S14 = 14 2 [2(9) + (14 - 1)(-2)] = (7)(18 - 26) = (7) × (-8) = - 56 Thus, sum of 14 terms of this AP is - 56.

Q. (i) the sum for the first n terms of an AP is ( 5 n 2 2 + 3 n 2 ) . Find hte nth term and the 20th term of this AP.

(ii) The sum of the first n terms of an AP is ( 3 n 2 2 + 5 n 2 ) . Find its nth term and the 25th term.

Solution:

(i) Sum of n terms, S n = 5 n 2 2 + 3 n 2

S 1 = 5 ( 1 ) 2 2 + 3 ( 1 ) 2 = 5 2 + 3 2 = 8 2 = 4 = a S 1 = 5 ( 2 ) 2 2 + 3 ( 2 ) 2 = 20 2 + 6 2 = 10 + 3 = 13 a 2 = S 2 − S 1 = 13 − 4 = 9 d = a 2 − a 1 = 9 − 4 = 5 a n = a + ( n − 1 ) d = 4 + ( n − 1 ) 5 = 4 + 5 n − 5 = 5 n − 1 a 20 = 5 n − 1 = 5 × 20 − 1 = 100 − 1 = 99

(ii) Sum of n terms, S n = 3 n 2 2 + 5 n 2

S 1 = 3 ( 1 ) 2 2 + 5 ( 1 ) 2 = 3 2 + 5 2 = 8 2 = 4 = a S 1 = 3 ( 2 ) 2 2 + 3 ( 2 ) 2 = 12 2 + 10 2 = 6 + 5 = 11 a 2 = S 2 − S 1 = 11 − 4 = 7 d = a 2 − a 1 = 7 − 4 = 3 a n = a + ( n − 1 ) d = 4 + ( n − 1 ) 3 = 4 + 3 n − 3 = 3 n + 1 a 25 = 3 n + 1 = 3 × 25 + 1 = 75 + 1 = 76

Q. How many terms of the AP: 21, 18, 15, ... must be added to get the sum 0?

Solution:

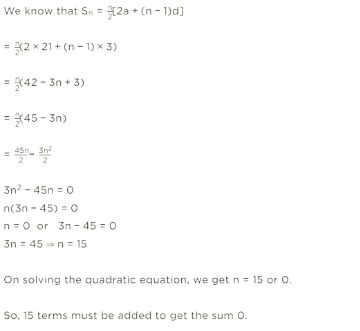
Q. How many terms of the AP 9, 17, 25, ... must be taken so that their sum is 636?

Solution:
A.P = 9,17,25 a=9 d=17-9 =8 Sum of n terms, S n = n 2 [ 2 a + ( n − 1 ) d ] 636 = n 2 [ 2 ( 9 ) + ( n − 1 ) 8 ] 636 = n 2 [ 18 + 8 n − 8 ] 636 = n 2 [ 10 + 8 n ] 1272 = 10 n + 8 n 2 8 n 2 + 10 n − 1272 = 0 2 [ 4 n 2 + 5 n − 636 ] = 0 4 n 2 + 5 n − 636 = 0 4 n 2 + 53 n − 48 n − 636 = 0 n ( 4 n + 53 ) − 12 ( 4 n + 53 ) = 0 ( n − 12 ) ( 4 n + 53 ) = 0 n − 12 = 0 n = 12 12 terms must be given to sum of 636

Q. How many terms of the AP 63, 60, 57, 54, ... must be taken so that their sum is 693. Explain the double answer.

Solution:
Given, AP 63, 60, 57 where, a = 63 and the difference (d) = 60 - 63 = -3 also given that S n = 693 ∴ to find a, we know S n = n 2 [ 2 a + ( n − 1 ) d ] By substituting the values of a, d and S n we get; 693 = n 2 [ 2 ×63 + (n - 1) - 3 ] 693 = n 2 [ 126 - 3n + 3 ] 693 = n 2 [ 129 - 3n ] 693 = 129 n 2 − 3 n 2 2 693 × 2 = 129n - 3 n 2 1386 = 129n - 3 n 2 1386 - 129n + 3 n 2 = 0 By dividing the whole equation by 3 we get, 1386 3 − 129 n 3 + 3 n 2 3 = 0 3 462 - 43n + n 2 = 0 ie; n 2 - 43n + 462 = 0 using factorisation method :-- sum = - 43 and product = 462 ∴ the numbers are -21 and -22 So by splitting the middle term we get; ( n 2 - 21n ) ( - 22n + 462 ) = 0 n ( n - 21 ) - 22 ( n - 21 ) = 0 ( n - 21 ) ( n - 22 ) = 0 ∴ n = 21 and n = 22 ie; We get the sum of the given AP as 693 when we take first 21 terms of it or 22 terms of the same AP. Verification of the Answer First take n as 21, the S 21 = 21 2 ( a + a 21 ) a 21 = a + ( 21 - 1 ) d = 63 + [ 20 × ( - 3 ) ] = 63 - 60 a 21 = 3 ∴ S 21 = 21 2 [ 63 + 3 ] = 21 2 × 66 S 21 = 693 So the condition is satisfied for when n = 21 Now check for when n = 22 S 22 = 22 2 ( a + a 22 ) a 22 = a + ( 22 - 1 ) d = 63 + [ 21 × ( -3 ) ] = 63 - 63 a 22 = 0 We know S 22 = S 21 + a 22 = 693 + 0 = 693 ∴ the condition is satisfied in both the cases so n = 21 or n = 22 Q. Find the sum of all odd numbers between 0 and 50.
Solution:
1st odd no.=1 last odd no.=49 a=1, an or l=49, common diff. d= 2, a n = a + ( n − 1 ) d =1+(n-1)2=49 =1+2n-2=49 =2n-1=49 =2n=49=1 =2n=50 n=25 S n = n 2 [ a + L ] = 25 2 ( 1 + 49 ) = 25 2 × 50 = 25 × 25 = 625 therefore sum of all odd integers between 0 to 50 is 625

Q. Find the sum of all natural numbers between 200 and 400 which are divisible by 7.

Solution:
The numbers lying between 200 and 400, which are divisible by 7, are 203, 210, 217, ­­­­­­­­… 399 ∴First term, a = 203 Last term, l = 399 Common difference, d = 7 Let the number of terms of the A.P. be n. ∴ a n = a + ( n − 1 ) d = 399 ⇒ 399 = 203 + (n –1) 7 ⇒ 7 (n –1) = 196 ⇒ n –1 = 28 ⇒ n = 29 S n = n 2 [ a + L ] S 29 = 29 2 [ 203 + 399 ] = 29 2 × 602 = 8729 Thus, the required sum is 8729.

Q. Find the sum  first forty positive integers divisible by 6.

Solution:
The positive integers divisible by 6 are 6,12,18,....... up to 40 terms the given series is in arthimetic progression with first term a=6 and common difference d=6 the sum of n terms of an A.p is Sum of n terms, S n = n 2 [ 2 a + ( n − 1 ) d ] = 40 2 × 2 ( 6 ) + ( 39 ) 6 = 20 12 + 234 = 20 × 246 = 4920

Q. Find the sum of the first 15 multiples of 8.

Solution:
The first 8 multiples of 8 are 8, 16, 24, 32, 40, 48, 56,64.......120 These are in an A.P., having first term as 8 and common difference as 8. Therefore, a = 8 d = 8 S 15 = ? S n = n 2 [2a + (n - 1)d] ⇒ S 15 = 15 2 ​​​​[2(8) + (15 - 1)8] ⇒ S 15 = 7.5[6 + (14) (8)] ⇒ S 15 = 7.5[16 + 112] ⇒ S 15 = 7.5(128) ⇒ S 15 = 960

Q. Find the sum of all three - digit natural numbers which are divisible by 13.

Solution:
As per question; AP: 104 , 117 , 130 ........... 988 a = 104 , a n = 988 ⇒ 988 = 104 + (n-1) 13 ⇒ 988 - 104 = (n-1)13 ⇒ 884 13 = n-1 ⇒ n= 69 S n = n 2 ( a + a n ) ⇒ S n = n 2 ( 104 + 988) ⇒ S n = 69 2 ( 1092 ) ⇒ S n = 37674

Q. The first and the last terms of an AP are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?

Solution:
Let a and d are the first term and the common difference for an AP respectively. Number of terms of AP = n Last term = nth term = l = a n a = 17 , d = 9 , l = 350 a + ( n - 1 ) d = 350 ⇒ 17 + ( n - 1 ) 9 = 350 ⇒ ( n - 1 ) 9 = 350 - 17 ⇒ ( n - 1 ) 9 = 333 ⇒ n - 1 = 333 9 ⇒ n - 1 = 37 ⇒ n = 37 + 1 ⇒ n = 38 Therefore, number of terms in given AP = n = 38 Sum of n terms of AP = S n S n = n over 2 ( a + l ) Here, n= 38 ⇒ S 38 = 19[ 17 + 350 ] ⇒ S 38 = 19 × 367 ⇒ S 38 = 6973

Q. In an AP, the first term is 22, nth term is -11 and sum of first n terms is 66. Find n and hence find the common difference.

Solution:

a c c o r d i n g space t o space q u e s t i o n a equals 22 a subscript n equals a plus open parentheses n minus 1 close parentheses d equals negative 11 a subscript n equals 22 plus open parentheses n minus 1 close parentheses d equals negative 11 minus negative negative open parentheses 1 close parentheses open parentheses n minus 1 close parentheses d equals negative 33 s u m space o f space n space t e r m s S subscript n equals n over 2 open square brackets 2 a plus open parentheses open parentheses n minus 1 close parentheses d close parentheses close square brackets equals 66 n over 2 open square brackets 2 cross times 22 minus 33 close square brackets equals 66 n open parentheses 44 minus 33 close parentheses equals 132 11 n equals 132 n equals 12 p u t space t h e space v a l u e space o f space n space i n space e q u open parentheses 1 close parentheses t h e n 22 plus open parentheses n minus 1 close parentheses d equals negative 11 22 plus 11 d equals negative 11 11 d equals negative 33 d equals negative 3

Q. In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees that each section of each class will plant will be double of the class in which they are studying. If there are 1 to 12 classes in the school and each class has two sections, find how many trees were planted by students. Which value is shown in the question?

Solution:
Given: The number of trees that each section of each class will plant will be double of the class in which they are studying. Number of classes are 12 ( 1 to 12 ), and each class has two sections. ⇒ Number of trees planted by the students of each section of class 1 = 1 × 2 = 2 There are two sections of class 1 . Therefore, Number of trees planted by the students of class 1 = 2 × 2 = 4 Number of trees planted by the students of each section of class 2 = 2 × 2 = 4 .---(1) There are two sections of class 2 . Therefore, Number of trees planted by the students of class 2 = 2 × 4 = 8 ---(2) Similarly, Number of trees planted by the students of class 3 = 2 × 6 = 12 ---(3) So, the number of trees planted by the students of different classes are 4 , 8 , 12 , . . . Therefore, Total number of trees planted by the students = 4 + 8 + 12 + . . . . up to 12 terms Lets evaluate, 4 + 8 + 12 + . . . . up to 12 terms. Here, 8 − 4 = 12 − 8 = . . . . = 4 Since, the difference of every consecutive terms is constant. So, this series is an arithmetic series. Here, a = 4 , d = 8 – 4 = 4 and n = 12 Since, the sum of first n - terms of an AP is,, S n = n 2 [ 2 a + ( n − 1 ) d ] ⇒ S 12 = 12 2 [ 2 × 4 + ( 12 – 1 ) × 4 ] ⇒ S 12 = 6 [ 8 + ( 11 × 4 ) ] ⇒ S 12 = 6 × [ 8 + 44 ] ⇒ S 12 = 6 × 52 ⇒ S 12 = 312 Therefore, the total number of trees planted by the students are 312 .

Q. In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are 10 Potatoes in the line. A competitor starts from the bucket, picks up the nearest potato runs back with it, drops it in the bucket, runs back to pick up the next potato runs to the bucket to drop it in, and the continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?

Solution:
The distances of potatoes from the bucket are 5, 8, 11, 14… Distance run by the competitor for collecting these potatoes are two times of the distance at which the potatoes have been kept. Therefore, distances to be run are 10, 16, 22, 28, 34,………. a = 10 d = 16 − 10 = 6 n = 10 S 10 = ? S 10 = 12 2 [ 2 ( 10 ) + ( n − 1 ) ( 6 ) ] = 12 2 [ 2 ( 10 ) + ( 10 − 1 ) ( 6 ) ] = 5 [ 20 + 54 ] = 5 ( 74 ) = 370 Therefore, the competitor will run a total distance of 370 m.
Q. There are 25 trees at equal distances of 5 m in a line with a water tank, the distance of the water tank from the nearest tree being 10 m. A gardener waters all the trees separately, starting from the water tank and returning back to the water tank after watering each tree to get water for the next, Find the total distance covered by the gardener in order to water all the trees.
Solution:
Distance covered by the gardener to water the first tree and return to the water tank = 10m + 10m = 20 m Distance covered by the gardener to water the second tree and return to the water tank = 15m + 15 m = 30 m Distance covered by the gardener to water the third tree and return to the water tank = 20m + 20m = 40 m Therefore, total distance covered by the gardener to water all the trees = 20m + 30m + 40m + ...... Up to 25 terms This is an arithmetic series. Here a = 20, d = 30 – 20 = 10 and n = 25 Using the formula, S n = n 2 [ 2 a + ( n − 1 ) d ] we get S 25 = 25 2 [ 2 × 20 + ( 25 – 1 ) × 10 ] = 25 2 × ( 40 + 240 ) = 25 2 × 280 = 3500 Hence, the total distance covered by the gardener to water all the trees is 3500 m.

Q. The 24th term of an AP is twice is 10th term. Show that its 72nd term is 4 times its 15 the term.

Solution:
Let first term = a and common difference = d we know that a n = a + ( n − 1 ) d Given that, a 24 = 2 × a 10 ⇒ a + ( 24 − 1 ) d = 2 × ( a + ( 10 − 1 ) d ) ⇒ a + 23 d = 2 × ( a + 9 d ) ⇒ a + 23 d = 2 a + 18 d ) ⇒ a = 5 d . . . . ( i ) Now 15th term, a 15 = a + ( 15 − 1 ) d = a + 14 d [ From (i) ] = 5 d + 14 d = 19 d Similarly 72nd term, a 72 = a + ( 72 − 1 ) d = a + 71 d = 5 d + 71 d = 76 d Now, a 72 a 15 = 76 d 19 d = 4 ∴ a 72 = 4 × a 15 Hence, 72 t h term is 4 times to its 15 t h term.

Benefits of RS Aggarwal Solutions for Class 10 Maths Chapter 11 Exercise 11.3

Clear Understanding: These solutions provide step-by-step explanations that clarify how to solve problems involving AP, helping students grasp concepts effectively.

Practice: By solving problems from Exercise 11.3 students can practice applying AP formulas and strengthen their problem-solving skills.

Comprehensive Coverage: The solutions cover various types of problems ensuring students are well-prepared for exams and assessments.

Self-assessment: Students can use these solutions to self-assess their progress and identify areas where they may need further practice or clarification.

RS Aggarwal Solutions for Class 10 Maths Chapter 11 Exercise 11.3 FAQs

What does Exercise 11.3 of RS Aggarwal's Class 10 Maths cover?

Exercise 11.3 focuses on determining the number of terms in an Arithmetic Progression (AP) and finding specific terms based on given information such as the first term, common difference, and last term.

How can Exercise 11.3 help in understanding AP?

By practicing Exercise 11.3, students can strengthen their understanding of AP concepts, including how to calculate the number of terms and find specific terms using AP formulas.

Why is it important to practice Exercise 11.3?

Practicing Exercise 11.3 helps students develop confidence in solving AP problems, improves their mathematical reasoning skills, and prepares them thoroughly for exams.

What is an Arithmetic Progression (AP)?

An Arithmetic Progression is a sequence of numbers where the difference between consecutive terms is constant.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Check out these Related Articles
BlogImage
CLASS 10 EXAM
Share
NCERT Solutions for Class 10 Social Science Geography Chapter 3 Water Resources
Read Full Story
28 Sept 2025, 08:42 pm
BlogImage
CLASS 10 EXAM
Share
RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.9 Pair of Linear Equations in Two Variables
Read Full Story
28 Sept 2025, 08:41 pm
BlogImage
CLASS 10 EXAM
Share
RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.7 PDF Download
Read Full Story
28 Sept 2025, 08:40 pm
BlogImage
CLASS 10 EXAM
Share
RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.8
Read Full Story
28 Sept 2025, 08:39 pm
BlogImage
CLASS 10 EXAM
Share
RD Sharma Solutions Class 10 Maths Chapter 3 Exercise 3.6
Read Full Story
28 Sept 2025, 08:38 pm
BlogImage
CLASS 10 EXAM
Share
CBSE Class 10 English Sample Paper 2024-25 PDF Download
Read Full Story
28 Sept 2025, 08:34 pm
BlogImage
CLASS 10 EXAM
Share
NCERT Solutions for Class 10 Social Science History
Read Full Story
28 Sept 2025, 08:24 pm
BlogImage
CLASS 10 EXAM
Share
RS Aggarwal Solutions for Class 10 Maths Chapter 17 Exercise 17.2
Read Full Story
28 Sept 2025, 08:20 pm
BlogImage
CLASS 10 EXAM
Share
CBSE Class 10 English Grammar Questions and Answers
Read Full Story
28 Sept 2025, 08:12 pm
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.