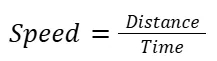Speed Time and Distance, Concept, Formulas, Tricks and Solved Questions

Speed, Time, and Distance

In banking and financial exams, problems involving speed, time, and distance are common as they test analytical and quantitative skills. These problems often involve practical scenarios like travel, work, or motion, requiring the application of the fundamental relationship between speed, time, and distance

Speed, Time, and Distance Formulas

Speed:

Definition: Speed is the rate at which an object covers a distance. It is a scalar quantity, meaning it only has magnitude and no direction.

Formula: 

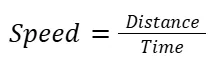
Types of Speed

1. Uniform Speed: When an object covers equal distances in equal intervals of time.

2. Variable Speed: When an object covers different distances in equal intervals of time.

3. Average Speed: The total distance traveled divided by the total time taken.

4. Downstream: When a boat moves in the direction of the current, its effective speed increases because the speed of the current adds to the speed of the boat in still water.

5. Upstream: When a boat moves against the direction of the current, its effective speed decreases because the speed of the current subtracts from the speed of the boat in still water. 

Formula for Average Speed:

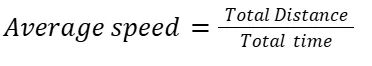
Formula for Downstream and Upstream speed:

1. Downstream Speed: Speed downstream = Speed of boat in still water + Speed of the current

2. Upstream Speed: Speed upstream = Speed of boat in still water − Speed of the current

Weightage of Speed, Time and Distance in Bank Exams

Preliminary Exams:

• Quantitative Aptitude Section: Speed, Time, and Distance problems often make up about 5-10% of the total questions in the Quantitative Aptitude section. This means that out of 35-50 questions, around 2-5 questions might be related to STD.

Main Exams:

• Quantitative Aptitude/Mathematics Section: In the main exams, the weightage can be slightly higher. Speed, Time, and Distance questions can constitute about 10-15% of the total questions. This could be around 5-8 questions in a section with 50-60 questions.

Speed, Time, and Distance Examples

1. Uniform Speed: 

Problem: A car travels a distance of 240 km in 4 hours. What is its speed?

Solution:

2. Average Speed: 

Problem: A person travels 150 km at 50 km/h and another 100 km at 25 km/h. What is the average speed for the entire journey?

Solution:

3. Relative Speed: 

Problem: Two trains are moving towards each other with speeds of 60 km/h and 40 km/h respectively. What is their relative speed?

Solution:

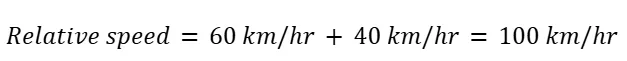
4. Meeting Point: 

Problem: Two cyclists start from two points 120 km apart and move towards each other at speeds of 30 km/h and 40 km/h respectively. How long will it take for them to meet?

Solution:

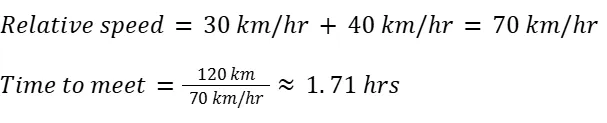
5. Upstream and Downstream: 

Problem: A boat's speed in still water is 10 km/h. If the speed of the current is 2 km/h, what is the boat's speed upstream and downstream?

Solution:

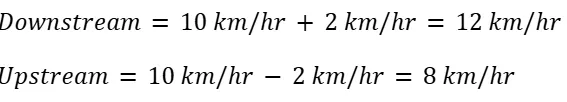
Time:

Definition: Time is the measure of the duration needed to travel a certain distance at a specified speed. It is typically measured in hours, minutes, or seconds.

Basic Formula:

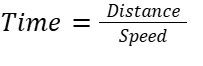
• Distance: The total length of the path traveled.

• Speed: The rate at which the distance is covered

Distance:

Definition: Distance is the measure of the space between two points along a path traveled. It does not consider the direction of travel, only the length.

Basic Formula:

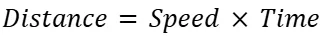
Speed: The rate at which the distance is covered (measured in units such as km/h, m/s).

Time: The duration over which the travel occurs (measured in units such as hours, and seconds)

Speed, Time, and Distance Solved Questions

Problem: A car travels at a speed of 60 km/h and covers a distance of 180 km. How long does it take to travel this distance?

Solution:

Problem: A car travels at a speed of 80 km/h for 3 hours. What is the distance covered? 

Solution:

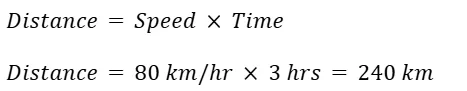
Problem: A cyclist travels at a speed of 12 km/h and takes 5 hours to cover a certain distance. What is the distance covered? 

Solution:

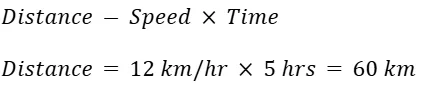
Speed, Time & Distance Conversions:

Note: For a certain distance, if the ratio of speeds is a: b, then the ratio of times taken to cover the distance would be b: a and vice versa. 

Problem: A person travels to a town at 40 km/h and returns at 60 km/h. If the total time for the round trip is 8 hours, find the distance between the two towns.

Solution:

Here the Distance is constant, so the Time taken will be inversely proportional to the Speed. Ratio of Speed is given as 40: 60, i.e. 2 : 3.

So the ratio of Time taken will be 2 : 3. 

Total Time taken = 8 hours; Time taken while going is 2 hours and returning is 3 hours. 

Hence, Distance = 40x2 = 80 km

Previous Year Questions Of Speed, Time, and Distance In Banking Exams

Q1.  A car travels from City A to City B at a speed of 60 km/h and returns at a speed of 40 km/h. If the total time taken for the round trip is 6 hours, what is the distance between the two cities?

Q2. A person travels from his home to a town at a speed of 50 km/h and returns at a speed of 75 km/h. If the total time for the round trip is 10 hours, find the distance between the home and the town.

Q3. A cyclist covers a distance of 96 km at a speed of 12 km/h. If the speed had been 4 km/h more, the cyclist would have saved 2 hours. What is the original time taken?

Q4. A person travels a distance of 240 km at a speed of 60 km/h. If he had traveled at 80 km/h, he would have saved 1 hour. What is the original time taken?

Q5.  Two trains start from the same point and travel in opposite directions. Train A travels at 70 km/h and Train B at 50 km/h. After 3 hours, the distance between them is 360 km. What is the distance traveled by Train A in 3 hours?

Q6. A person covers a distance of 180 km in 3 hours. If he increases his speed by 10 km/h, he will cover the same distance in 2 hours. Find the original speed.

Q7. A train travels 120 km at a speed of 80 km/h. If the speed were increased by 20 km/h, it would take 30 minutes less to cover the same distance. Find the original time taken.

Q8. Two cars start from the same point and travel in the same direction. Car A travels at 60 km/h and Car B at 80 km/h. After 5 hours, Car B is 100 km ahead of Car A. What is the distance traveled by Car A in 5 hours?

Q9.  Two trains start from different stations and travel towards each other at speeds of 90 km/h and 110 km/h. If they meet after 4 hours, what is the distance between the two stations?

Q10. A man travels from point A to point B at a speed of 15 km/h and returns from point B to point A at a speed of 20 km/h. If the total time for the round trip is 6 hours, find the distance between the two points.

Banking Exam Online Course – Join Today!!