
parallelogram theorem
Area of parallelograms of Class 9
POLYGONAL REGION
Polygon region can be expressed as the union of a finite number of triangular regions in a plane such that if two of these intersect, their intersection is either a point or a line segment. It is the shaded portion including its sides as shown in the figure.
(a) Area Axioms:
Every polygonal region R has an area, measure in square unit and denoted by ar(R).
-
(i) Congruent area axiom :if R1 and R2 be two regions such that R1
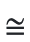 R2 then ar(R1) = ar (R2).
R2 then ar(R1) = ar (R2).
-
(ii) Area monotone axiom :If R1
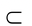 R2, then are (R1)
R2, then are (R1)
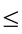 ar(R2).
ar(R2).
-
(iii) Area addition axiom :If R1 are two polygonal regions, whose intersection is a finite number of points and line segments and R = R1
 R2, then ar (R) = ar(R1) + ar(R2).
R2, then ar (R) = ar(R1) + ar(R2).
- (iv) Rectangular area axiom :If AB = a metre and AD = b metre then, ar (Rectangular region ABCD) = ab sq. m.
(b) Unit of Area :
There is a standard square region of side 1 metre, called a square metre, which is the unit of area measure. The area of a polygonal region is square metres (sq. m or m2) is a positive real number
AREA ADDITION AXIOM:
Total area R of the plane figure ABCD is the sum of two polygonal regions R1 and R2, i.e. ar. (R) = ar.
THEOREM 1
A diagonal of parallelogram divides it into two triangles of equal area.
Given: A parallelogram ABCD whose one of the diagonals is BD.
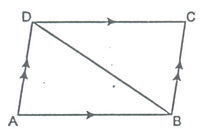
To prove: ar (ΔABD) = ar (ΔCDB).
Proof: In ΔABD and ΔCDB.
AB = DC [Opp. sides of a ||gm]
AD = BC [Opp. sides of a ||gm]
BD = BD [Common side]
∴ ΔABD≅ΔCDB [By SSS]
∴ ar (ΔABD) = ar(ΔCDB) [Congruent area axiom] Hence Proved.
THEOREM 2
Prove that parallelogram on the same base and between same parallel are equal in area.
Given: Parallelogram ABCD and ABEF are on the same base AB and between the same parallels AB and CF.
To Prove: ar. (ABCD) = ar. (ABEF)
Proof: In ΔADF and ΔBCE, we have
AF = BE [Opposite sides of the ||gms]
∠AFD = ∠BEC [Corresponding angles]
∠ADF = ∠BCE [Corresponding angles]
∴ ΔADF≅ΔBCE [By AAS Congruence]
⇒ ar. (ΔADF) = ar. (ΔBCE) [Congruence area axiom]
Adding ar.(quadrilateral ABED) to both sides, we get
ar. (ΔADF) + ar.(quadrilateral ABED) = ar (ΔBCE) + ar.(quadrilateral ABED)
⇒ ar. ||gmABEF = ar. ||gmABCD [Area addition axiom]
THEOREM 3
Prove that parallelogram and a rectangle on the same base and between the same parallels are equal in area.
Given :A Parallelogram ABCD and a rectangle ABML are on the same base AB and between the same parallels AB and CL.
To Prove : ar. ||gmABCD = ar. rectangle ABML.
Proof :In ΔADL and ΔBCM, we have
AL = BM [Opposite sides of a rectangle]
∠ALD =∠BMC[Corresponding angles]
∠ADL = ∠BCM [Corresponding angles]
∴ ΔADL≅ΔBCM [By AAS congruence]
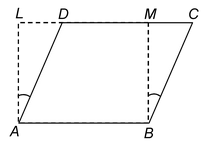
⇒ ar. (ΔADL) = ar. (ΔBCM)
Adding ar. (quadrilateral ABMD) to both sides, we get
ar. ΔADL + ar. quadrilateral ABMD = ar. ΔBCM + ar. quadrilateral ABMD
or ar. of rectangle ABML = ar. of ||gmABCD.
THEOREM 4
If a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.
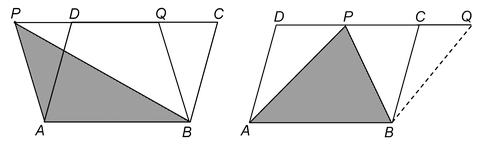
(i) (ii)
Given: AParallelogram ABCD and a triangle APB are on the same base AB and between the same parallels AB and PC.
To Prove: ar.
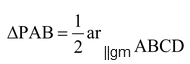
Const: Through B draw BQ || AP which meets PC or PC produced at Q. Join BQ
Proof: Since the parallelogram ABQP and the parallelogram ABCD stand on the same base AB and between same parallels AB and PQ or DQ.
∴ ar. ||gmABQP = ar. ||gmABCD [By theorem 1] …(i)
Since the diagonal of a ||gmABQP divides it into two Δs of equal area
∴ ar. ||gmABQP = 2 ar. (ΔPAB) …(ii)
From (i) and (ii), we have
2 ar. (ΔPAB) = ar. ||gmABCD
⇒ ar.
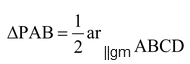 .
.
THEOREM 5
The arc of parallelogram is the product of its base and the corresponding altitude.
Given: A||gm ABCD in which AB is the base and AL is the corresponding height.
To prove: Area (||gmABCD) = AB × AL.
Construction:
Draw BM
 DC so that rectangle ABML is formed.
DC so that rectangle ABML is formed.
Proof: ||gm ABCD and rectangle ABML are on the same base AB and between the same parallel lines AB and LC.
∴ ar(||gmABCD) = ar(rectangle ABML) = AB × AL.
∴ area of a ||gm = base × height.
Ex: Prove that a diagonal of a parallelogram divides it into two triangles of equal area.
Solution: Given: A parallelogram ABCD in which BD is one of the diagonals.
To prove → ar((ΔABD) = ar((ΔCDB)
Proof:
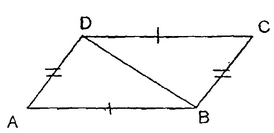
In triangles ABD and CDB, we have
AB = CD (in a parallelogram opposite sides are of equal length)
AD = CB
and BD = DB (common side)
⇒ΔABD (ΔCDB (by SSS)
Hence by congruent area axiom ar((ΔABD) = ar((ΔCDB).
Ex. A parallelogram ABCD and a rectangle ABPQ are on the same base AB and between the same parallels AB and CQ. If AB = 8 cm and AQ = 6 cm, find the area of ||gmABCD.
Sol. A rectangle is a parallelogram in which each angle is 90° and parallelogram on the same base and between same parallels are equal in area.
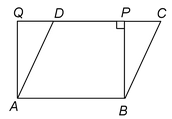
∴ ar. (||gmABCD) = ar. (rectangle ABPQ)
But ar. (||gmABPQ) = AB×AQ
= (8 × 6) cm 2 = 48 cm 2
∴ Area of parallelogram ABCD = 48 cm 2 .
Ex. In a parallelogram ABCD, AB = 8 cm. The altitudes corresponding to sides AB and AD are respectively 4 m and 5 cm. Find AD.
Sol. We know that, Area of a parallelogram = Base × Corresponding altitude
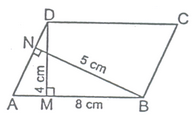
∴ Area of parallelogram ABCD = AD × BN = AB × DM
⇒ AD × 5 = 8 × 4
⇒ AD =
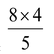
= 6.4 cm. Ans.
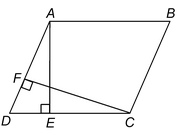
Ex. In figure, ABCD is a parallelogram, AE⊥CD and CF⊥AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
Sol. AB = 16 cm, AE = 8 cm and CF = 10 cm, AD= ?
ar. ||gmABCD (on base AD) = ar. ||gmABCD (on base CD)
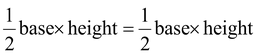
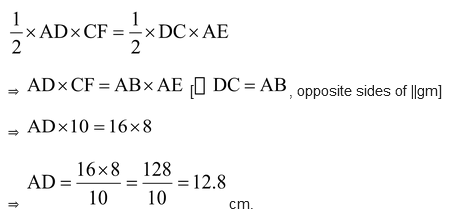
Ex: ABCD is a quadrilateral and BD is one its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.
Sol: In ΔABD and ΔCDB
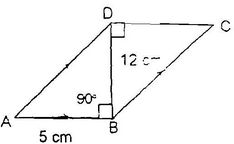
∠ABD = ∠CBD = 90o (alternate interior angles are equal)
∠ADB = ∠CBD
∠BDA = ∠BDC
Hence, ABCD is a parallelogram.
Now, area of parallelogram ABCD = (base ×corresponding altitude)
⇒area of parallelogram ABCD = AB × BD = 5 ×12 sq. units = 60 sq. cms.
Ex: Prove that parallelograms on the same base and between the same parallel lines are equal in area.
Sol: Given: Two parallelogram ABCD and PBCQ having same base BC and between the same parallel lines BC and AQ.
To Prove: ar(parallelogram ABCD)= ar (parallelogram PBCQ)
Proof: In triangles ABP and DCQ,
∠BAP = ∠CDQ
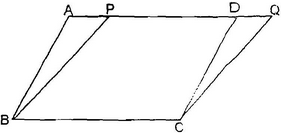
(Corresponding angles when AQ intersects parallel lines AB and DC).
∠BPA = ∠CDQ
(Corresponding angles when AQ intersects parallel lines BP and CQ).
AB = DC (Opposite sides of a parallelogram)
∴ΔABP ≅ ΔDCQ (AAS)
Hence area ΔABP = area ΔDCQ
or, area ΔABP + area BPDC = area ΔDCQ + area Δ BPDC
∴ar (parallelogram ABCD) = ar (parallelogram PBCQ).
Related Topics






