Mind Map
Area of parallelograms of Class 9
AREA OF A QUADRILATERAL
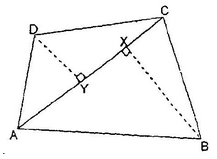
Let ABCD be any quadrilateral. Draw a diagonal AC. From B and D, draw perpendiculars BX and DY to AC.
Let AC = d, BX = p, DY = q
.
 Area of quadrilateral ABCD = Area of
Area of quadrilateral ABCD = Area of 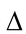 ABC + Area of
ABC + Area of 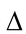 ADC
ADC
= 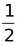 AC
AC  BX +
BX + 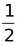
 AC
AC  DY =
DY = 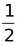 dp +
dp + 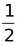 dq =
dq = 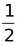 d (p + q)
d (p + q)
Ex:A quadrilateral ABCD is such that the diagonal BD divides its area into two equal parts.
Prove that BD bisects AC.
Sol: Let ABCD be a parallelogram having diagonals AC and BD. We have to prove that AC and BD bisect each other at O. i.e. AO = OC.

Draw AL  BD and CM
BD and CM  BD.
BD.
BD divides area ABCD into two equal parts.
 ar(ΔABD) = ar (ΔBDC) (given)
ar(ΔABD) = ar (ΔBDC) (given)
Thus, ΔABD and ΔBDC are on the same base AB are of equal area. Therefore, their, corresponding altitudes are equal.
i.e. AL = CM.
inΔALO and ΔCMO,
∠1 = ∠2 (vertically opposite angles)
∠ALO = ∠CMO (each equal to 90o)
and AL = CM
ΔALO ≅ ΔCMO (AAS)
That means AO = OC (CPCT)
 BD bisects AC.
BD bisects AC.
Ex: Find the area of quadrilateral ABCD (given √5 = 2.23)
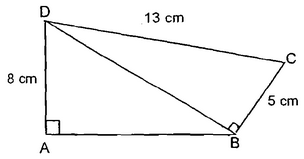
Sol: In ΔBCD, CD2 = BD2 + BC2
⇒ (13)2 = (BD)2 + 52 ⇒ BD = 12
In ΔABD, BD2 = AB2 + AD2
⇒ (12)2 = (AB)2 + 82 ⇒ AB = 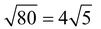
 ar(quad. ABCD) = ar(ΔABD) + ar(ΔBCD)
ar(quad. ABCD) = ar(ΔABD) + ar(ΔBCD)
= 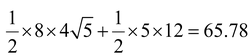 cm2.
cm2.
Ex: In the adjoining figure, AB || DC, DA is perpendicular to AB. Further DC = 7 cm,
CB = 10 cm, AB = 13 cm. Find the area of quadrilateral ABCD.

Sol: Draw CM  AB, then
AB, then
AM = 7 cm, MB = 13 – 7 = 6 cm
BC = 10 cm
 from right triangle MBC
from right triangle MBC
MC =  (by Pythagoras theorem)
(by Pythagoras theorem)
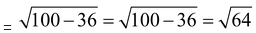 = 8 cm.
= 8 cm.
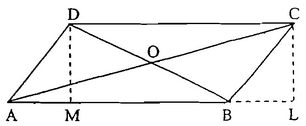
Area of ABCD = 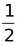 (13 + 7) 8 = 80 cm2.
(13 + 7) 8 = 80 cm2.
Ex: Show that the area of a rhombus is half the product of the lengths of its diagonals.
Sol: Let ABCD be a rhombus whose diagonals AC and BD intersect at O.
As the diagonals of a rhombus intersect at right angles
 OB
OB  AC and OD
AC and OD  AC.
AC.
Area (ABCD) = area (ΔABC) + area (ΔADC)

 .
.
Ex: If the diagonals AC and BD of a quadrilateral ABCD intersect at O and separate the quadrilateral ABCD into four triangle of equal area, show that the quadrilateral is a parallelogram.
Sol: Given: a quadrilateral ABCD, whose diagonals AC and BD intersect at O in such a way that
ar(ΔAOB) = ar(ΔBOC)
= ar(ΔAOD) = ar(ΔCOD)
To prove: ABCD is a ||gm.
Construction: Draw CL  AB and DM
AB and DM  AB
AB
Proof: ar(ΔAOD) = ar(ΔBOC)
⇒ar(ΔAOD) + ar(ΔAOB) = ar(ΔBOC) + ar(ΔAOB)
⇒ar(ΔABD) = ar(ΔABC)
⇒
⇒ DM = CL
⇒ DC || AB
Similarly, AD || BC
 ABCD is a parallelogram.
ABCD is a parallelogram.
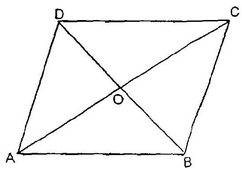
Area of Trapezium:
ABCD is a trapezium in which AB || CD (AB < CD).
AL and BM are perpendiculars on CD from vertices A and B respectively.
Let AL = BM = h.
Area ABCD = Area of rectangle ABML + Area of  ADL + Area of
ADL + Area of 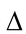 BMC
BMC
=
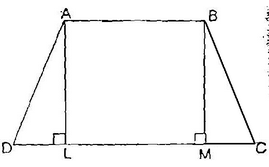
= 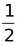 h(2AB + DL + MC) =
h(2AB + DL + MC) = 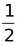 h {AB + (LM + DL + MC)} (as AB = LM)
h {AB + (LM + DL + MC)} (as AB = LM)
= 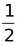 h(AB + CD)
h(AB + CD)
 Area of trapezium =
Area of trapezium = 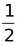 ×height
×height  (the sum of parallel sides) = h/2(a + b)
(the sum of parallel sides) = h/2(a + b)
Where a = AB, b = CD, h = AL or BM.
Ex: Find the sum of the length of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
Sol: Area = 4.2 m2
Height = 280 cm = 2.8 m
b1 + b2 = m.
Ex. If ABCD is a quadrilateral in which diagonals bisect at right angles and ACBD, then it is a
(a) Isosceles trapezium (b) Trapezium
(c) Rhombus (d) None
Sol. C
In ΔADO and CDO
OD = OD, OA = OC
AOD = ∠COD = 90°
ADO ≅ABO (S.A.S)
AD = CD
Similarly AD = BC = CD = AB
As digonals AC, BD are not equal, ABCD is a rhombus.
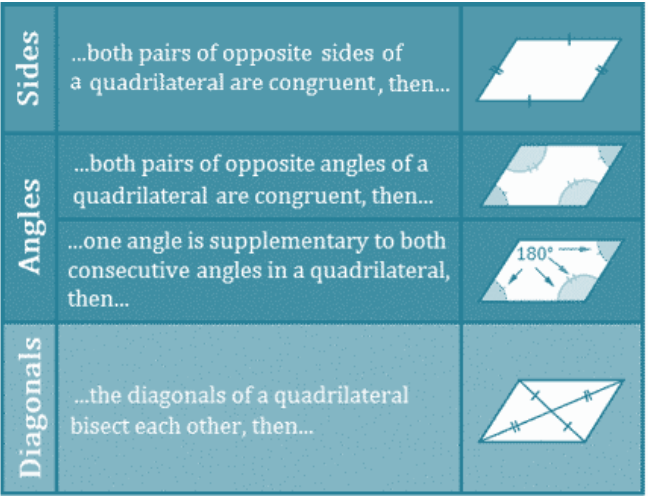
Important Types of Quadrilaterals Rectangles Squares Parallelograms Rhombus Trapezoid (trapezium) Kites The definitions are important.
CONGRUENCE AREA AXIOM
- If ΔABC≅ΔDEF
Then, ar. (ΔABC) = ar. (ΔDEF)
- Two Congruent figures have equal area but the Converse is not always true.
- Area of a parallelogram is the product of its base and the corresponding altitude.
- Area of a triangles is half the product of its base and the corresponding altitude.
- Triangles on the same base and between the same parallels are equal in area.
- A median of a triangle divides it into two triangles of equal area.
AREA ADDITION AXIOM
Total area R of the plane figure ABCD is the sum of two polygonal regions R1 and R2.
i.e. ar. (R) = ar. ar.
- Parallelogram on the same base and between same parallel are equal in area.
- Parallelogram and a rectangle on the same base and between the same parallels are equal in area.
- If a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is equal to half the area of the parallelogram.









