

Before delving into the concept of Integration by Substitution , it's essential to understand what integration is. Integration is a fundamental concept in calculus, and it involves finding the antiderivative of a given function. The integral of a function f(x) is represented as F(x) and is expressed as:
∫f(x)dx = F(x) + C
Here R.H.S. of the equation means integral of f(x) with respect to x.
- F(x)is referred to as the antiderivative or primitive of the function.
- dx is the integrating agent, indicating that the integration is with respect to the variable
- f(x) is called the integrand, which is the function being integrated.
- C represents the constant of integration or arbitrary constant, which arises due to the indefinite nature of integration.
- x is the variable of integration, showing the variable with respect to which the integration is performed.
While we know the antiderivatives of basic functions, this method is limited to handling basic functions. To find the integrals of more complex functions, we use various methods of integration. One such method is Integration by Substitution.
We have a good understanding of the antiderivatives of elementary functions, making it relatively straightforward to compute their integrals. However, this approach is primarily applicable to basic functions. To tackle the integration of more complex functions, we employ diverse techniques of integration. One such technique we will explore is Integration by Substitution.
Integration by Substitution Method
In the technique of integration by substitution, we transform a given integral into a more manageable form by replacing the independent variable with another variable.
Consider an equation that involves an independent variable
an equation having an independent variable in x, i.e. ∫sin (x 3 ).3x 2 .dx———————–(i),
In the equation given above the independent variable can be transformed into another variable say t.
Substituting x 3 = t ———————-(ii)
Differentiation of above equation will give-
3x 2 .dx = dt ———————-(iii)
Substituting the value of (ii) and (iii) in (i), we have
∫sin (x 3 ).3x 2 .dx = ∫sin t . dt
Thus the integration of the above equation will give
∫sin t . dt= -cos t + c
Again putting back the value of t from equation (ii), we get
∫sin (x 3 ).3x 2 .dx = -cos x 3 + c
The General Form of integration by substitution is:
∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x)
Integration by substitution is a powerful technique that comes in handy when we replace a function with its derivative, which is also found within the integral. This substitution simplifies the function, making it amenable to straightforward application of basic integration formulas.
Regenerate
Also Check – Data Handling Formula
When to Use Integration by Substitution Method?
In the realm of calculus, the integration by substitution method goes by alternative names such as the "Reverse Chain Rule" or the "U-Substitution Method." This technique proves valuable when dealing with integrals structured in a specific form:
∫ f(g(x))·g'(x)·dx = ∫ f(u)·du
In this approach, you begin by integrating the function with respect to the substituted value (f(u)), and then you conclude the process by substituting back the original function g(x).
Also Check – Sets Formula
Integration by Substitution Example
Example 1 :
Solve the integration of
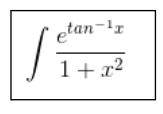
Solution:
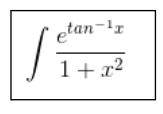
Given :
Let t = tan -1 x …… (1)
dt = (1/ 1+x 2 ) . dx
I = ∫ et . dt
= et + C …….(2)
Substituting the value of (1) in (2), we have I = e tan-1x + C. This is the required integration for the given function.
Also Check – Ratio and Proportion Formula
Example 2:
Integrate 2x cos (x 2 – 5) with respect to x .
Solution:
I = ∫2xcos(x 2 – 5).dx
Let x 2 – 5 = t …..(1)
2x.dx = dt
Substituting these values, we have
I = ∫cos(t).dt
= sin t + c …..(2)
Substituting the value of 1 in 2, we have
= sin (x 2 – 5) + C
Integration by Substitution Formula FAQs
Q1. What is Integration by Substitution?
Q2. Why is it called the "Reverse Chain Rule"?
Q3. When is Integration by Substitution most useful?
Q4. Can Integration by Substitution be used for definite integrals as well?
Q5. Are there any specific guidelines for choosing the right substitution?











