
Ratio and Proportion Formula are The concept of ratios and proportions is fundamental in mathematics and plays a crucial role in various real-world scenarios. This article delves into the explanation and application of these concepts, shedding light on their significance and how they relate to different situations.
The concept of ratio serves as a means of comparing two quantities that share the same nature. The formula for expressing the ratio between two numbers denoted as "a" and "b," can be depicted as either "a: b" or "a/b." When multiple ratios possess equality, they are considered to be in proportion. This notion of ratio and proportion finds its basis in the realm of fractions. These foundational concepts of ratio and proportion play a pivotal role in numerous other mathematical principles. Moreover, ratio and proportion find practical utility in resolving various every day predicaments. For instance, they are employed in comparing attributes like height, weight, distance, or time. Similarly, they prove invaluable in tasks such as combining ingredients while cooking, among others.
Also Read - Cubes and Cubes Roots Formula
What is Ratio and Proportion?
A ratio arises from the division-based comparison of two quantities, while the state of equality between two ratios is recognized as proportion. A ratio can be expressed in distinct formats, such as x : y or x/y, and it is conventionally verbalized as "x is to y."
In contrast, proportion presents itself as an equation signifying the equivalence of two ratios. This relationship is symbolized as x : y : : z : w, and its verbal interpretation is "x is to y as z is to w." In this context, the stipulation holds that x/y = z/w, under the condition that w and y are both non-zero.
Also Read - Comparing Quantities Formula
Definition Of Ratio
Ratios are a way to compare the quantities of two or more related items. Expressed in the form of a fraction or with a colon, ratios provide insight into the relative sizes or quantities of different elements. For example, in a recipe, the ratio of flour to sugar might be 2:1, signifying that there are twice as many units of flour as there are units of sugar.
A ratio emerges from the contrast between two quantities, achieved by dividing the initial quantity by the latter one. Assuming a and b are two similar quantities with matching units, where b holds a value other than 0, the outcome of a divided by b, denoted as a/b, is identified as the ratio linking a to b. Ratios are denoted by employing the colon symbol (:). It is noteworthy that the ratio a/b remains dimensionless and can be depicted in the form of a : b.
Also Read - Coordinate Geometry Formula
Definition Of Proportion
Proportion pertains to the balance of two ratios. Whenever two ratios are equivalent, they inherently exhibit proportion. Proportions are indicated using the symbol (: :), and they serve as a means to determine unknown values. Essentially, proportion takes the form of an equation or statement signifying the equality of two ratios or fractions. In the context of four distinct non-zero quantities – a, b, c, d – they are deemed proportional if a : b = c : d.
Consider two instances: 3 : 5 and 15 : 25. The ratio 3 : 5 can be transformed into 3/5 or 0.6, while 15 : 25 can be reconfigured as 15/25, equivalent to 3/5 or 0.6. Because both ratios hold equivalence, it is valid to assert their proportionality.
Two primary categories of proportions exist:
- Direct Proportion
- Inverse Proportion.
Direct Proportion
Direct proportion delineates the straightforward correlation between two quantities. When one quantity experiences augmentation, the other quantity follows suit, and conversely, when one decreases, so does the other. Consequently, an explicit notation for direct proportionality is y ∝ x. As an illustration, consider the scenario where a car's velocity escalates – this action leads to the car traversing an increased distance within an unchanging time interval.
Download PDF Ratio and Proportion Formula
Inverse Proportion
Inverse proportion characterizes the connection between two quantities wherein an augmentation in one quantity prompts a reduction in the other, and conversely, an increase in one leads to a decrease in the other. Consequently, an accurate representation of inverse proportionality takes the form of y ∝ 1/x. As an illustration, contemplate the situation where a vehicle's speed escalates – this occurrence leads to the vehicle traversing a consistent distance in a diminished period of time.
Ratio and Proportion Formula
The representation of a ratio is given as a : b ⇒ a/b, with the following meanings:
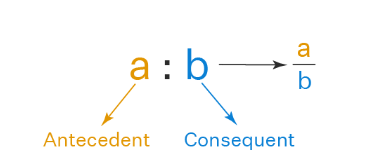
a represents the initial term or antecedent.
b represents the subsequent term or consequent.
For instance, the ratio 2 : 7 can also be symbolized as 2/7, where 2 serves as the antecedent and 7 as the consequent.
Formula for Ratios
When aiming to express a proportion involving two ratios, a : b and c : d, it can be depicted as:
a:b::c:d
Within this framework, b and c are termed mean terms,
while a and d are referred to as extreme terms.
In the case of a: b = c : d, it's crucial that quantities a and b are of identical nature with matching units.
However, c and d can each independently belong to the same category and units. For instance, 5 kg : 15 kg = Rs. 75 : Rs. 225.
Formula for a proportion
can be expressed as a/b = c/d or a : b : : c : d.
Notably, in proportion, the product of the mean terms equals the product of the extreme terms. This yields b × c = a × d in the proportion formula a: b : : c : d. For example, in 5 : 15 :: 75 : 225, the outcome is 15 × 75 = 5 × 225.
Difference Between Ratio and Proportion
A contrast between ratio and proportion is evident in the subsequent table.
| Ratio | Proportion |
|---|---|
| It serves to assess the magnitude of two quantities sharing identical units. | It serves to articulate the connection between two ratios. |
| The symbols employed for indicating a ratio encompass a colon (:), | The symbols employed for indicating a ratio encompass a colon (:), |
| It is denoted as an expression. | It is denoted as an equation |
Points to remember
- Any two quantities that share equivalent units can be subjected to comparison.
- Only when two ratios are identical are they deemed to be in proportion.
- To ascertain the equality and proportionality of two ratios, the cross-product method can also be employed.
- Should each term of a ratio be multiplied and divided by the same number, the ratio remains unaltered.
- Whenever the ratio between the first and second quantities equals the ratio between the second and third quantities, for any three given quantities, they are classified as existing in a continued proportion.
- Similarly, considering any set of four quantities in a continued proportion, the ratio between the first and second quantities is tantamount to the ratio between the third and fourth quantities.
Ratio and Proportion Formula FAQs
What Does the Ratio Formula Refer To?
How Can the Ratio Formula Be Expressed?
What Formula Can Be Used to Determine the Proportion of a Value?
Utilizing the Proportion Formula, Calculate the Value of x in the Proportion x : 32 :: 78 : 64.










