NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4
Get detailed NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4. Find step-by-step solutions to practice problems on triangles, including important concepts and formulas to enhance your understanding and improve exam preparation.
Ananya Gupta8 Jan, 2025
Share
NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4: NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4 focus on applying coordinate geometry concepts to calculate areas of triangles formed by given vertices. These solutions provide a clear, step-by-step explanation for solving problems, helping students grasp the application of formulas and properties effectively. By practicing these solutions, students can enhance their problem-solving skills, build a strong conceptual foundation, and perform well in board exams.
NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4 Overview
Exercise 7.4 of Chapter 7 (Coordinate Geometry) focuses on the application of coordinate geometry in finding the area of a triangle when the coordinates of its vertices are provided. The problems in this exercise are created to help students:- Apply the formula to calculate the area of a triangle.
- Verify if three points are collinear by checking if the area of the triangle is zero.
- Strengthen their understanding of basic coordinate geometry concepts through practical applications.
NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4 PDF
The NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4 PDF provides detailed solutions to all the questions in the exercise, which focuses on finding the area of a triangle when the coordinates of its vertices are given. It guides students step-by-step on how to apply the formula for the area of a triangle in coordinate geometry and checks for the collinearity of points. These solutions are designed to help students grasp the concept more effectively and are an excellent resource for revision and practice. You can download the PDF from the link provided below to access the solutions for all the questions.NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4 PDF
NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Exercise 7.4
Below is the NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4-Solve the followings Questions.
1. Determine t]“1he ratio in which the line 2x + y -4 =0 divides the line segment joining the points A(2,-2) and B(3,7).Answer:
Let the given line divide the line segment joining the points A(2, −2) and B(3, 7) in a ratio k : 1 Coordinates of the point of division =
This point also lies on 2x + y - 4 = 0
⇒
⇒
⇒ 9k - 2 = 0
⇒ k = 2/9
Therefore, the ratio in which the line 2x + y - 4 = 0 divides the line segment joining the points A(2, −2) and B(3, 7) is 2:9.
2. Find a relation between x and y if the points (x,y),(1, 2)and (7, 0)are collinear.
Answer:
If the given points are collinear, then the area of triangle formed by these points will be 0. Area of triangle =
Area =
0 = 1/2 [2x - y + 7y - 14]
0 =1/2 [2x + 6y - 14]
[2x + 6y - 14] = 0
x + 3y - 7 = 0
This is the required relation between x & y.
3. Find the centre of a circle passing through the points (6,-6), B(3,-7)and (3, 3).
Answer:
Let O (x,y) be the centre of the circle. And let the points (6, −6), (3, −7), and (3, 3) be representing the points A, B, and C on the circumference of the circle.
However OA = OB (Radii of same circle)
⇒
.png)
=>x² + 36 - 12x + y² + 36 + 12y = x² + 9 - 6x + y² + 49 -14y
⇒ -6x + 2y + 14 = 0
⇒ 3x + y = 7 ....1
Similary OA = OC (Radii of same circle)
=>x² + 36 - 12x + y² + 36 + 12y = x² + 9 - 6x + y² + 9 - 6y
⇒ -6x + 18y + 54 = 0
⇒ -3x + 9y = -27 .....(2)
On adding equation (1) and (2), we obtain
10y = - 20
y = - 2
From equation (1), we obtain
3x − 2 = 7
3x = 9
x = 3
Therefore, the centre of the circle is (3, −2).
4. The two opposite vertices of a square are (-1,2) and (3,2). Find the coordinates of the other two vertices.
Answer
Let ABCD be a square having (−1, 2) and (3, 2) as vertices A and C respectively. Let (x,y), (x
1
,y
1
) be the coordinate of vertex B and D respectively.
We know that the sides of a square are equal to each other.
∴ AB = BC
.png)
=>x² + 2x + 1 + y² -4y + 4 = x² + 9 -6x + y² + 4 - 4y
⇒ 8x = 8
⇒ x = 1
We know that in a square, all interior angles are of 90°.
In ΔABC,
AB² + BC² = AC²
.png)
⇒4 + y² + 4 − 4y + 4 + y² + 4 − 4y = 16
⇒2y² + 16 − 8 = 16
⇒2y² - 8 = 0
⇒y(y - 4) = 0
⇒y = 0 or 4
We know that in a square, the diagonals are of equal length and bisect each other at 90°. Let O be the mid-point of AC. Therefore, it will also be the mid-point of BD
Coordinate of point O = ((-1+3)/2, (2+2)/2)
⇒1 + x1/2 = 1
⇒1 + x1 = 2
⇒x1 = 1
and y + y
1 /2 = 2
⇒ y + y1= 4
⇒If y = 0
⇒y1= 4
⇒If y = 4
⇒y1= 0
Therefore, the required coordinates are (1, 0) and (1, 4).
5. The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of △ PQR if C is the origin? Also calculate the area of the triangle in these cases. What do you observe?
Answer:
(i) Taking A as the origin, AD and AB as the coordinate axes. Clearly, the points P, Q and R are (4, 6), (3, 2) and (6, 5) respectively. (ii)Taking C as the origin, CB and CD as the coordinate axes. Clearly, the points P, Q and R are given by (12, 2), (13, 6) and (10, 3) respectively. We know that the area of the triangle (POR) =.png)
= 1/2 [4(2-5) + 3(5-6) + 6(6-2)]
= 1/2 [-12 -3 +24]
= 9/2 sq. units
(ii) Taking C as origin, CB as x- axis, and CD as y- axis, the coordinates of vertices P, Q, and R are (12, 2), (13, 6), and (10, 3) respectively.
area of the triangle (PQR) =
= 1/2[12(6-3) + 13(3-2) + 10(2-6)
= 1/2 [36+13-40]
= 9/2 sq. units
Hence, the areas are same in both the cases.
6. The vertices of a △ ABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that AD/AB = AE/AC = 1/4 .Calculate the area of the △ ADE and compare it with the area of △ ABC.
Answer:
Given that (AD)/(AB) = (AE)/(AC) = 1/4
(AD)/(AD+DB) = (AE)/(AE+EC) = 1/4
(AD)/(DB)=(AE)/(EC) = 1/3
Therefore, D and E are two points on side AB and AC respectively such that they divide side AB and AC in a ratio of 1:3
Coordinates of Point D =
= (13/4, 23/4)
Coordinates of Point E =
= (19/4, 20/4)
Area of triangle =
Area of ΔADE =
=
Area of ΔABC = 1/2[4(5-2) + 1(2-6) + 7(6-5)]
= 1/2[12 - 4 + 7]
= 15/2
Clearly, the ratio between the areas of ΔADE and ΔABC is 1:16.
7. Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of △ ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2: 1.
(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ: QE = 2: 1 and CR : RF = 2 : 1.
(iv) What do you observe?
(Note: The point which is common to all the three medians is calledcentroid and this point divides each median in the ratio 2: 1)
(v) If A(x
1
,y
1
), B(x
2
,y
2
),and C(x
3
,y
3
),are the vertices of △ ABC, find the coordinates of the centroid of the triangle.
Answer:
(i) Median AD of the triangle will divide the side BC in two equal parts.
Therefore, D is the mid-point of side BC
Coordinate of D = (6 +1/2, 5 + 4/2) =(7/2,9/2)
(ii) Point P divides the side AD in a ratio 2:1.
Coordinate of P =
= (11/3 , 11/3)
(iii) Median BE of the triangle will divide the side AC in two equal parts.
Therefore, E is the mid-point of side AC.
Coordinate of E = (4+1/2, 2+4/2) = (5/2,3)
Point Q divides the side BE in a ratio 2:1.
Coordinate of Q =
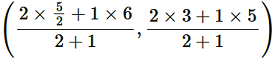= (11/3 , 11/3)
Median CF of the triangle will divide the side AB in two equal parts. Therefore, F is the mid-point of side AB
Coordinate of F = (4+6/2, 2+5/2) = (5,7/2)
Point R divides the side CF in a ratio 2:1.
Coordinate of R =
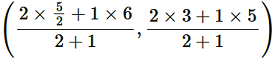= (11/3 , 11/3)
(iv) It can be observed that the coordinates of point P, Q, R are the same.
Therefore, all these are representing the same point on the plane i.e., the centroid of the triangle.
(v) Consider a triangle, ΔABC, having its vertices as A(x
1
,y
1
), B(x
2
,y
2
) and C(x
3
,y
3
)
Median AD of the triangle will divide the side BC in two equal parts. Therefore, D is the mid-point of side BC.
Coordinate of D =
Let the centroid of this triangle be O.
Point O divides the side AD in a ratio 2:1.
Coordinate of O =
=
8. ABCD is a rectangle formed by joining points A(-1,-1), B (-1,4), C (5,4) and D (5,-1). P, Q, R and S are the mid-points of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? Or a rhombus? Justify your answer.
Answer:
P is the mid point of side AB
Therefore the coordinates of P are ((-1-1)/2,(-1+4)/2) = (-1, 3/2)
Similary the coordinates of Q , R and S are (2,4),(5, 3/2), and (2, -1) respectilvely
Length of PQ =
Length of QR =
Length of RS =
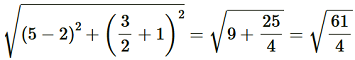Length of SP =
Length of PR =
= 6
Length of QS =
= 5
It can be observed that all sides of the given quadrilateral are of the same measure. However, the diagonals are of different lengths. Therefore, PQRS is a rhombus.
Benefits of Solving NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4
Conceptual Clarity : The exercise helps students understand the application of coordinate geometry concepts, particularly the formula for the area of a triangle and determining collinearity of points. Step-by-Step Learning : Solving these solutions ensures a structured approach to problems, improving analytical and logical thinking. Exam Readiness : This exercise includes important questions frequently asked in board exams, making it a great tool for preparation. Problem-Solving Skills : By solving various problems, students enhance their ability to tackle real-world problems using mathematical techniques. Practice and Precision : Regular practice with these solutions helps in minimizing errors and improving accuracy in calculations. Confidence Boost : Mastery of Exercise 7.4 concepts boosts confidence in solving geometry-based problems during exams.NCERT Solutions for Class 10 Maths Chapter 7 Exercise 7.4 FAQs
What is covered in Exercise 7.4 of NCERT Class 10 Maths?
Exercise 7.4 focuses on calculating the area of a triangle using coordinate geometry and verifying the collinearity of points by checking if the area is zero.
How do NCERT Solutions for Exercise 7.4 help students?
NCERT Solutions provide step-by-step explanations and detailed calculations, making it easier for students to understand and apply the concepts effectively.
Can these solutions help in competitive exams preparation?
Yes, the concepts from this exercise are foundational for various competitive exams like NTSE, Olympiads, and entrance tests, making the solutions a valuable resource.
How can I verify the accuracy of my answers for Exercise 7.4?
By cross-checking your solutions with the provided NCERT Solutions, you can ensure your answers are accurate and match the required steps.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App
