Fundamental Principles of Counting

FUNDAMENTAL PRINCIPLES OF COUNTING

(a) Multiplication Principle

There are m ways in doing a job and n ways of doing another job, then number of ways of doing both the jobs together is m × n.

(b) Addition Principle

Under the above situation, number of ways of doing either one job or the other
is m + n.

(ii) The number of ways of arranging n distinct objects in a row taking r(0 ≤ r ≤ n) at a time is nPr = n(n − 1)……(n − r + 1)

=

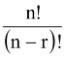
which obviously means that

ⁿP₀ = 1, ⁿP₁ = n and ⁿP_n − 1 = ⁿP_n = n!

(iii) The number of ways of arranging n distinct objects along a circle is (n − 1)!.

(iv) The number of ways of arranging n beads along a circular wire = .

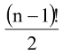(v) The number of permutation of n things taken all at a time, p being alike of one kind, q of another kind, r of the third kind and the remaining n − (p + q + r) are all different is .

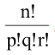(vi) Number of ways of distributing 'n' distinct things among 'r' persons such that there is no restriction on number of things received by a person is rn.

(vii) The number of ways of selecting r(0 ≤ r ≤ n) objects out of n distinct objects is denoted by nCr = 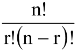, if r > n then nCr = 0.

Note the following facts.

(a) ⁿC₀ = ⁿC_n = 1 (b) ⁿCr = _nC_{n − r}

(c) ⁿCr + _nC_{r - 1} = ^{n + 1}Cr (d) ⁿCx = ⁿC_y ⇔ x = y or x + y = n

(e) ⁿCr = 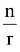× ^{n - 1}C_{r - 1} (f)

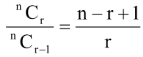
(viii) The number of ways of selecting at least one object out of n distinct objects = 2n - 1.

(ix) The number of combination of r things (r ≤ n) out of n identical things is 1.

 (x) The number of ways of selecting r objects from n objects = (r + 1), r = 0, 1, 2….. n.

(xi) The number of combinations of n distinct objects taking r at a time when k particular objects always occur is ^{n - k}C_{r - k}. If k particular objects never occur then the number of combinations of n distinct objects taken r at a time is ^{n - k}Cr_.

(xii) If out of p + q + r + s things, p are alike of one kind, q alike of the other kind and r alike of the third kind and s are different then the total number of ways of selecting at least one thing is (p + 1) (q + 1) (r + 1)2s − 1.

(xiii) The number of factors of n = 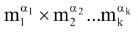, where m₁, m₂, ….. mk are different primes is (α₁ + 1) (α₂ + 1) …. (αk + 1).