
TYPES OF PROPORTION
Direct and inverse proportions of Class 8
There are four types of proportion
- Direct Proportion
- Inverse Proportion
- Compound Proportion
- Continued Proportion
Direct Proportion
Suppose the price of one piece of soap is 20 Rs. If a person wants to buy one dozen pieces of soap, then he has to pay 240 Rs. If he wants to buy two dozen pieces of soap, he has to pay 480 Rs and so on. We can easily see that if the person buys more pieces, he has to pay more or he has to pay less if he buys less pieces.
That is, as pieces of soap are increased total price also increased, conversely, if pieces of soap are decreased total price also decreased. In such situation, we say that pieces and price are directly related.
In other words, If increase in one quantity causes increase in other quantity or decrease in one quantity causes decrease in other quantity, then we say that they are related directly (They are direct proportion).
If and are in direct proportion, then division of and will be constant.
In the above example, we see that each ratio is the same.
Hence, if we are dealing with quantities, which are related directly, (which are in direct proportion), then we shall use the follow rule.
24 x 240 = 12 x 480 In general
Principle of Direct Proportion
Q1. If 30 dozens of eggs cost 300 Rs. Find the cost of 5-dozens of eggs.
Ans: Let be the required price of 5 dozens eggs
Since quantities are in direct proportion, so we use the above principle.
30x = 5 x 300
x = 1500/30
x= 50 Rs.
Q2. A car travel 81 km in 4.5 liters. How far will it goes by 20 liters of petrol.
Ans: Let be required distance travelled by car in 20 liters.
Since quantities are related directly, so by the above principle
4.5 x = 20 x 81
= 360 km
The Direct Proportion questions are usually of the form, "If x results in a, what will be the result if x changes to y? You need a simple 4 step approach to solve the problems:
Identify Variables
Usually this is a simpler thing to do. The variables are fairly obvious in typical proportion problems.
Understand the Relationships
Is the relationship between variables directly Proportional? Sometimes this information will not be provided. You need to understand the context and use common sense. For example the following relationships are directly proportional
- The quantity of goodies money can buy. More money lets you buy more. Right?
- The distance a car covers in a given time is directly proportional to its speed. Higher the speed, longer the car travels.
- The weight of a cylinder is directly proportional to its height. Higher the cylinder the more it weighs.
- The length of a shadow to the height
- The length between two points on a map to the actual distance
Express the Proportionaility
Get the problem to a form: "If x results in a, what will be the result if x changes to y?"
Q1. A stopwatch is defective and shows a time of 55 seconds for every minute. If this stop watch is used in an experiment and shows a time of 3 Minutes and 40 seconds, what time has actually elapsed (1 minute = 60seconds)?
(A) 2 Minutes 30 seconds
(B) 3 Minutes
(C) 3 Minutes 30 seconds
(D) 4 Minutes
(E) 5 Minutes
Ans. Step 1: The two variables the time shown on the watch and the real time are directly proportional.
Step 2: The proportionality is 55 Seconds: 1 Minute = 3 Minutes and 20 seconds: ?
To make things simple, lets convert the minutes to seconds. We know 1 Minute = 60 Seconds. Therefore 3 minutes and 40 seconds is equal to 3 × 60 + 40 = 220 seconds
If the actual elapsed time is x, we get:
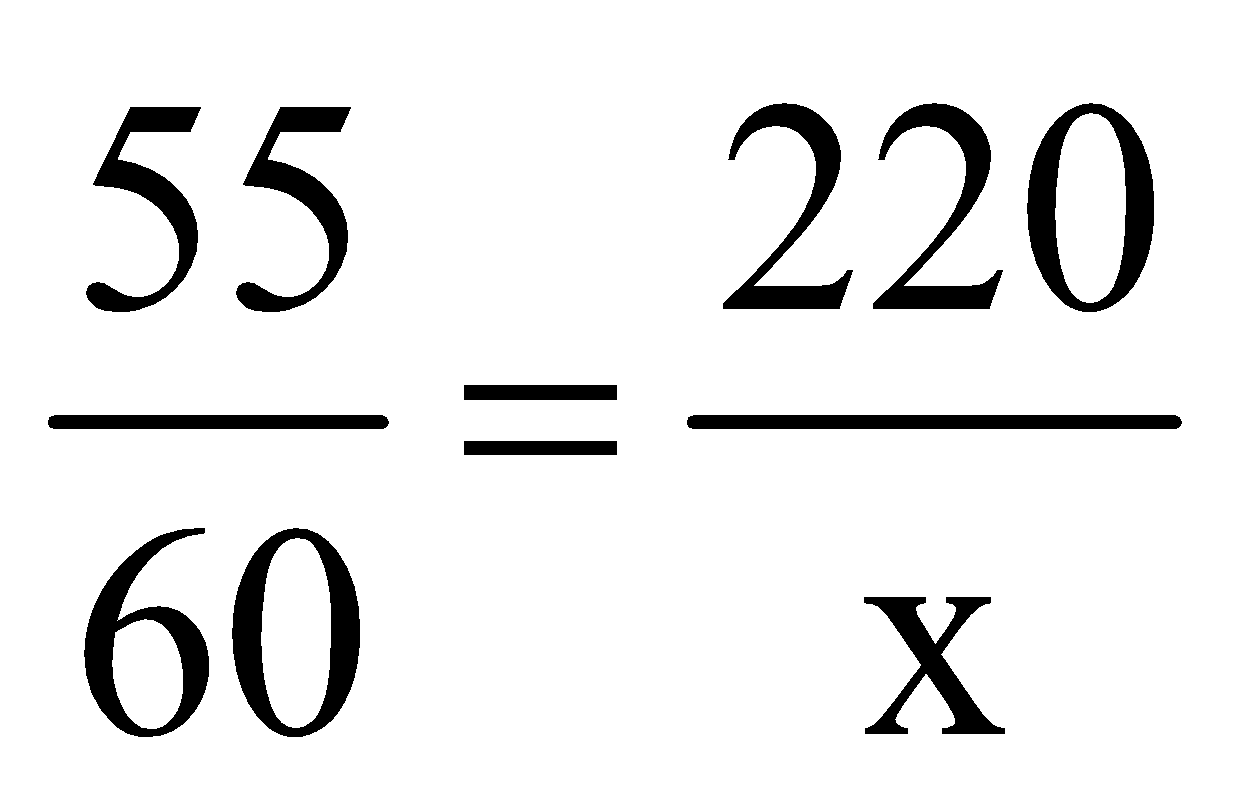
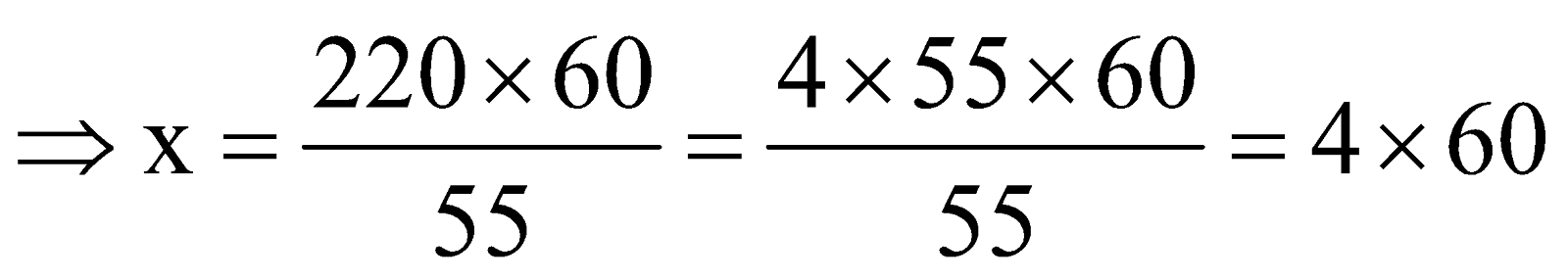
This time is in seconds. Since 1 minute = 60 seconds, the actual time elapsed is 4 minutes
The correct answer is D
Inverse Proportion
The concept of inverse proportion means that as the absolute value or magnitude of one variable gets bigger, the absolute value or magnitude of another gets smaller, such that their product is always the same.
Suppose that 20 men build a house in 6-days. If men are increased to 30 then they take 4-days to build the same house. If men become 40, they take 2-days to build the house.
| No. of men | No. of Days |
| 20 | 6 |
| 30 | 4 |
| 40 | 3 |
It can be seen that as the no. of men is increased, the time taken to build the house is decreased in the same ratio.
In other words,
If increased in one quantity causes decrease in other quantity or decrease in one quantity, then we say that both quantities are inversely related.
More explicitly, If two quantities x and y are in inverse proportion, then their product will be constant.
i.e. xy = c where c = constant
In the above example, we see that 20 x 6 = 120 30 x 4 = 120 40 x 3 = 120
Shows each product is constant or same.
Therefore, if we are dealing with quantities, which are related inversely, the we can use the following rule.
No. of Men No. of Days
20 ↔ 6
= 30 ↔ 4
20 x 6 = 30 x 4
In general,
No. of Men No. of days
a ↔ c
b ↔ d
ac = bd or
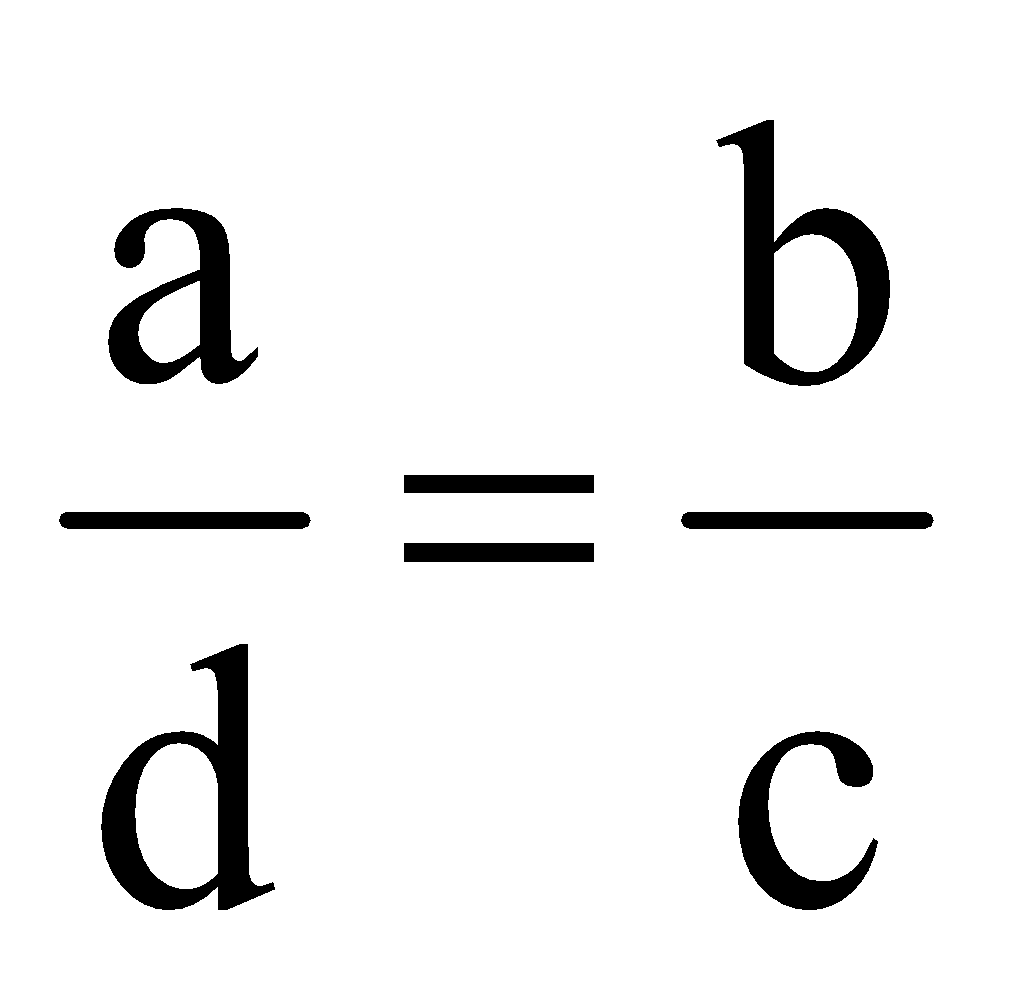
Q1. Four pipes can fill a tank in 70 minutes. How long will it take to fill the tank by 7 pipes?
Ans. No. of Pipes Time Taken
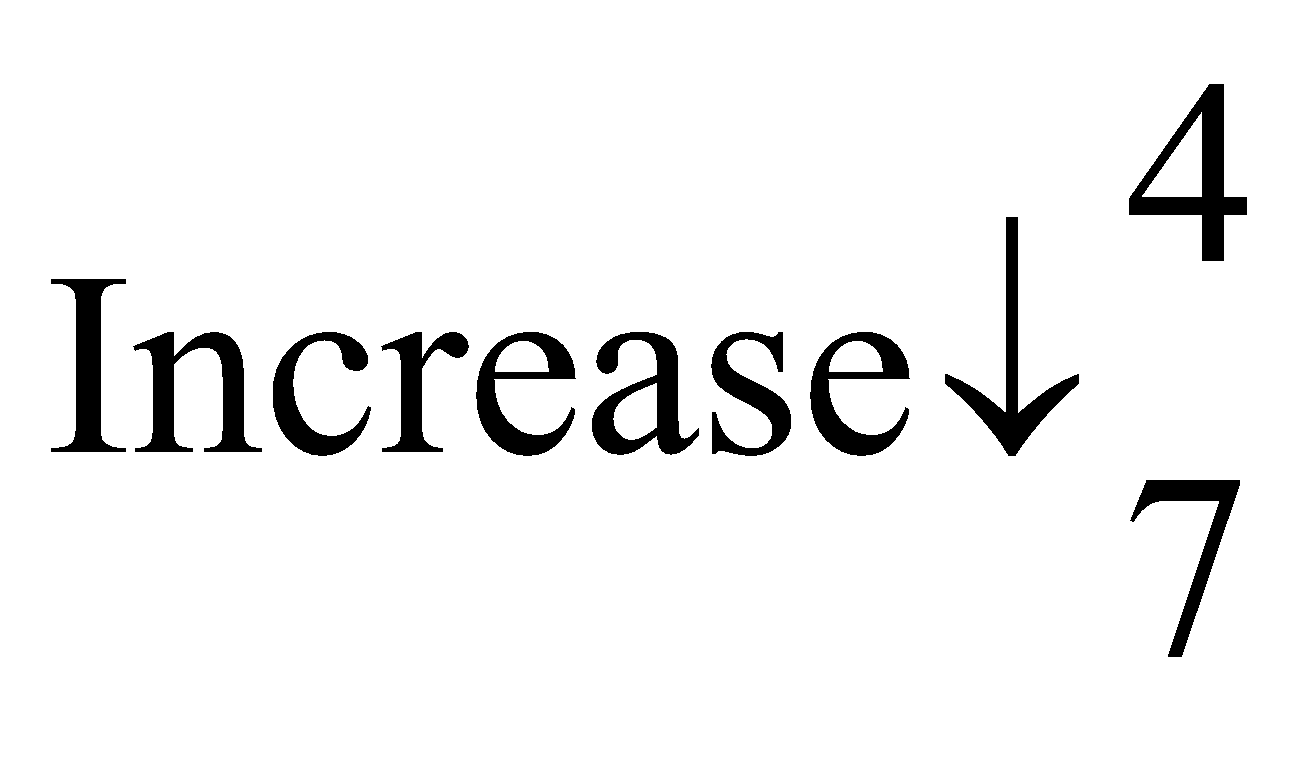

By the principle of inverse proportion, we have
4 x 70 = 7 × x
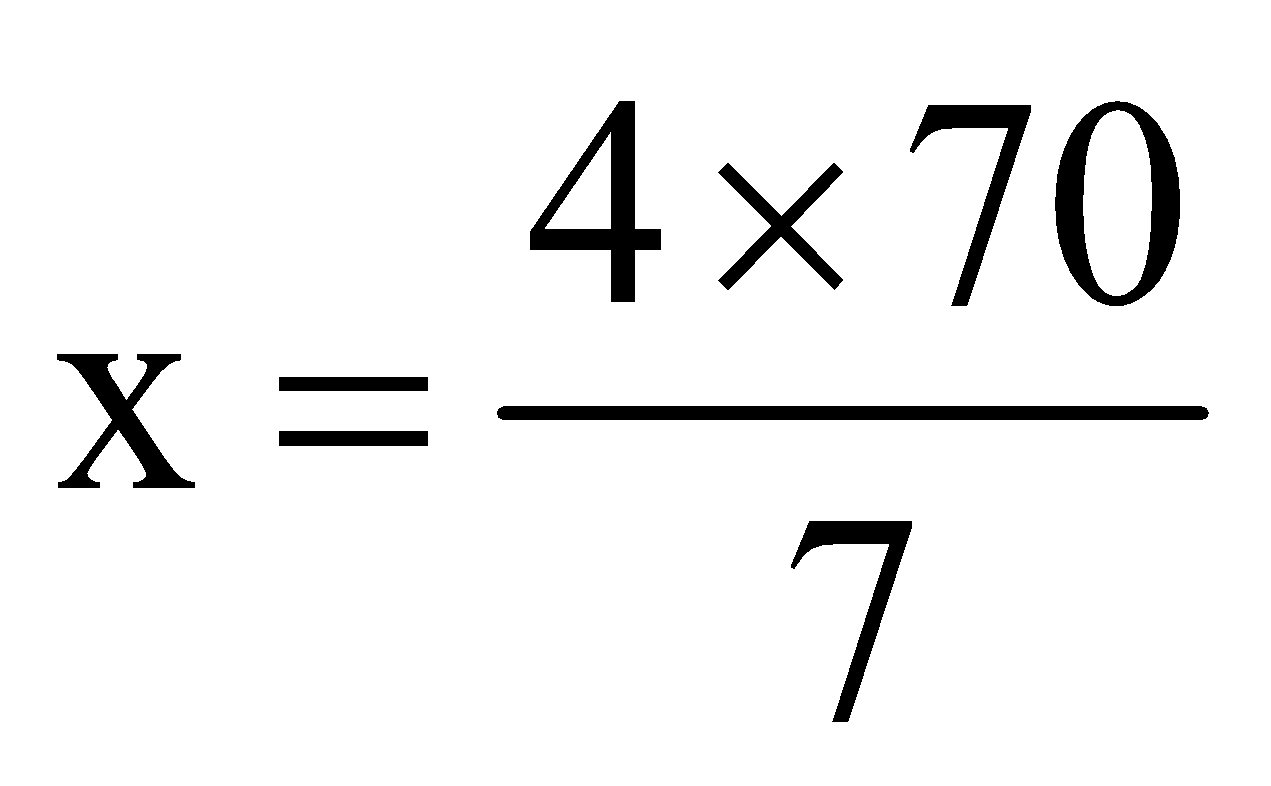 = 40 minutes
= 40 minutes
Q2. Thirty-five workers can build a house in 16-days. How many days will 28 workers working at the same rate take to build the same house?
Ans. No. of workers No. of days
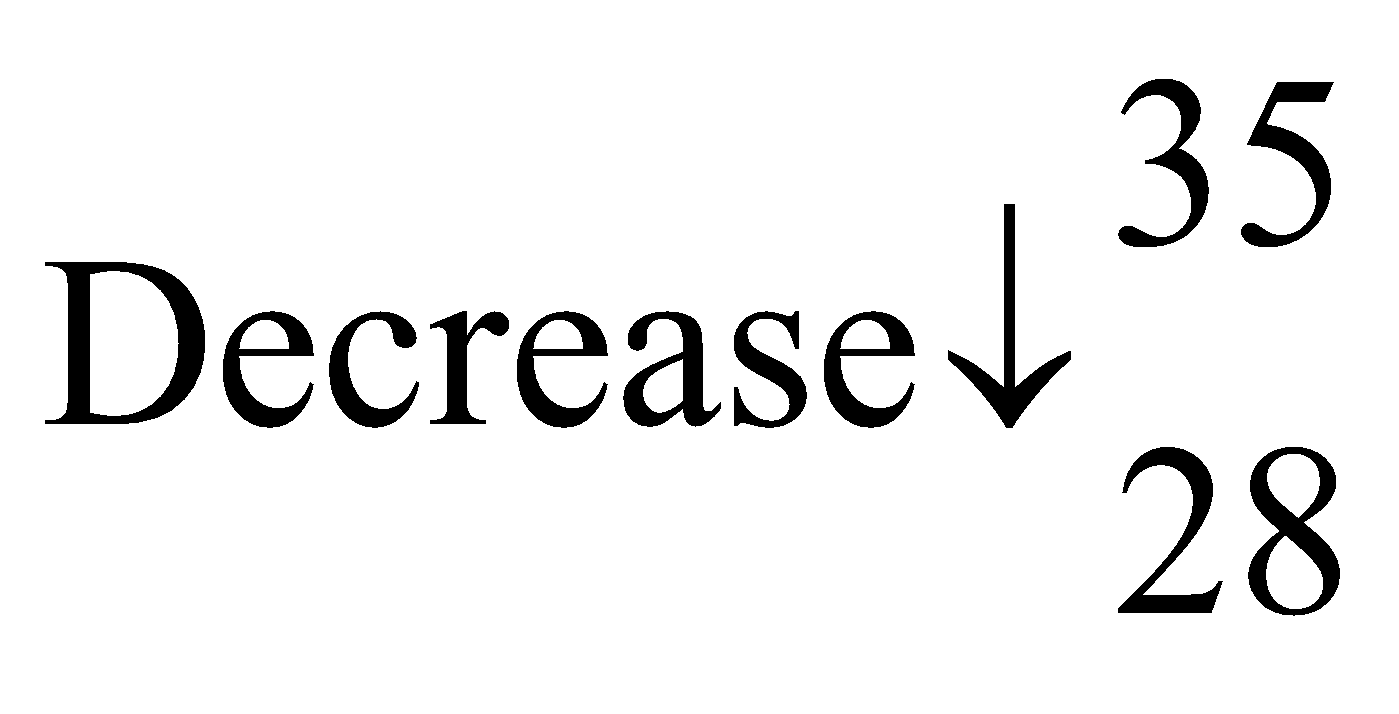
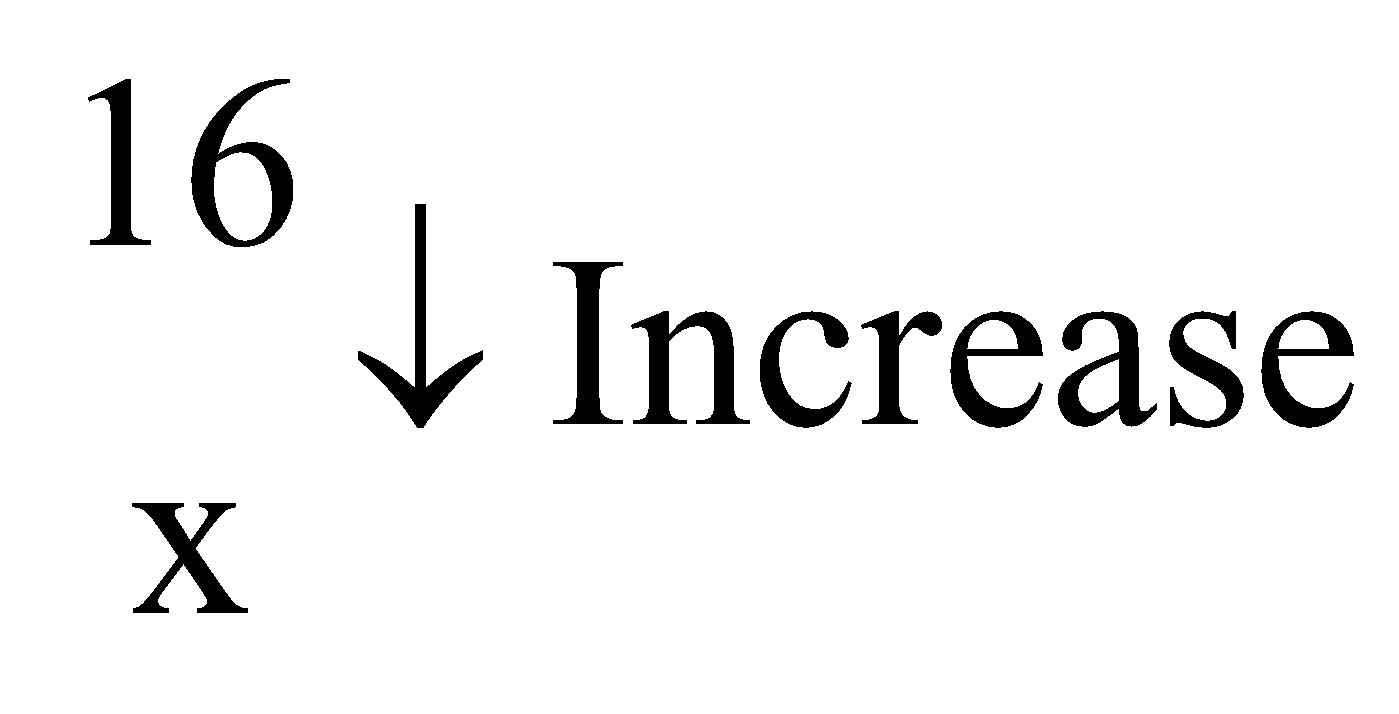
By the principle of inverse proportion, we have
28 × x = 35 ×16
x =
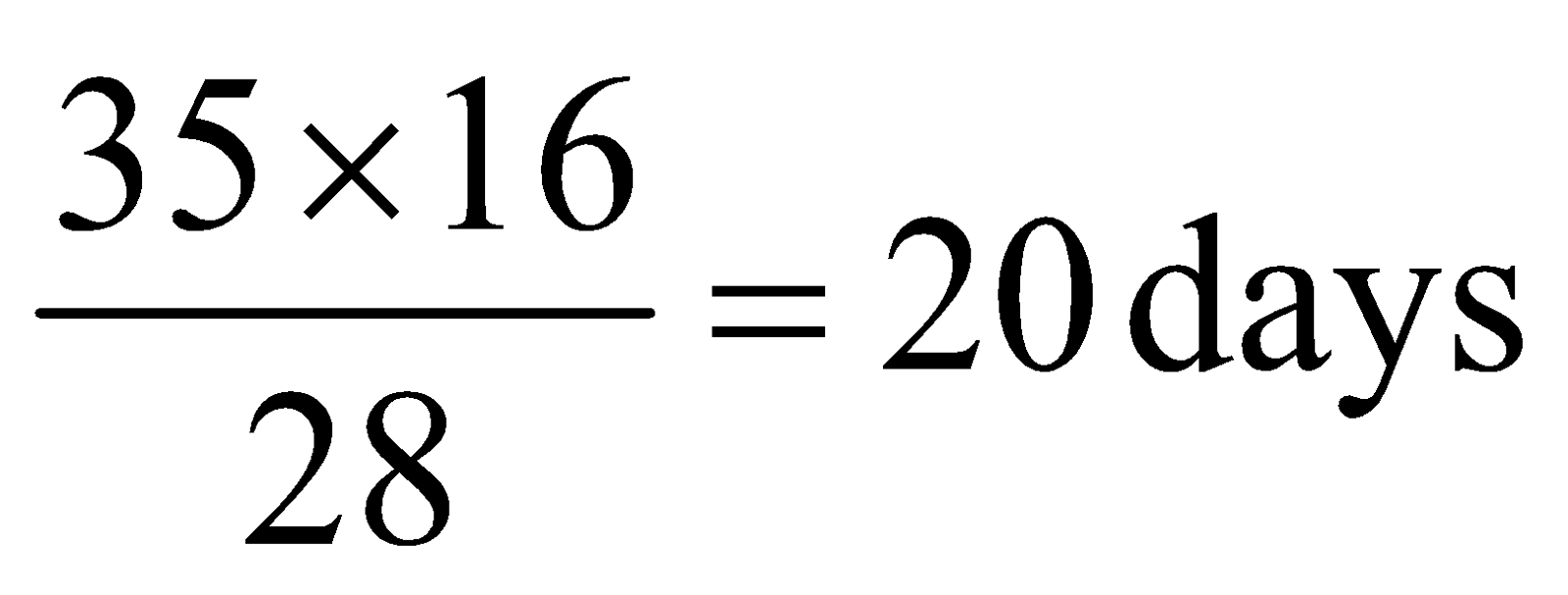
Q3. Imran brought 40 toys each cost Rs.14. How many toys Imran can buy at Rs.8 each from the same amount?
Ans. Price of toy No. of toys
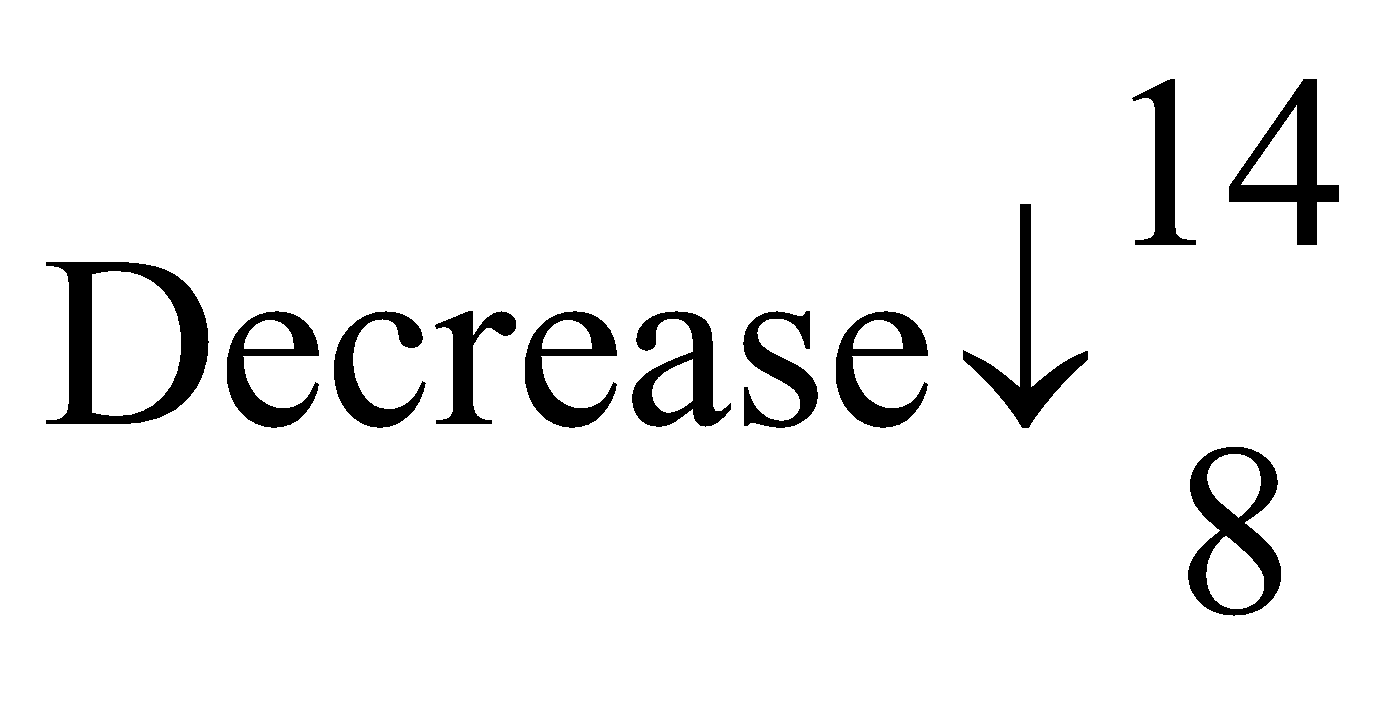

By the principle of inverse proportion, we have
14 x 40 = 8 × x
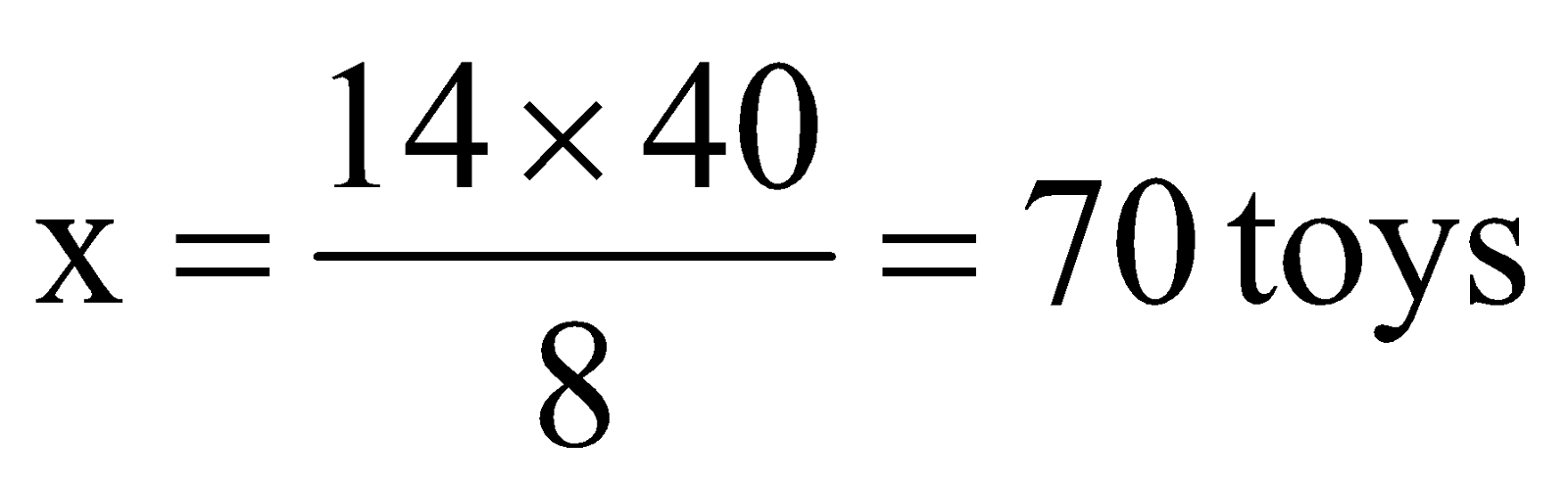
|
|
The symbol = represents ‘proportional to’. So if y is directly proportional to x, we write y ∝ x. (‘Directly proportional’ is used rather than just ‘proportional’ because there are several different types of proportionally as you will see below.) We can write y ∝ x as an equation y = kx, where k is a constant (does not depend on x or y). |
There are several other types of proportionality:
y is inversely proportional to x → y ∝
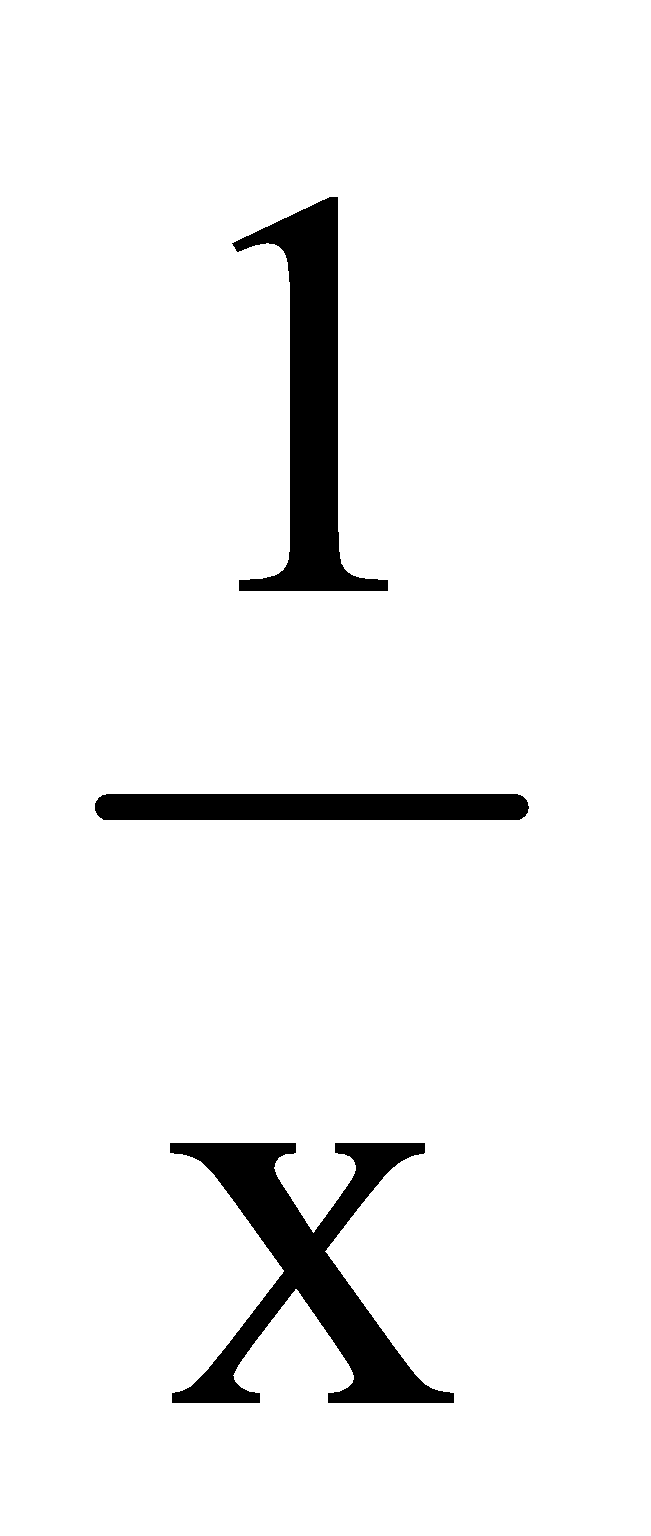 or y =
or y =
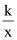
y is inversely proportional to x2 → y ∝
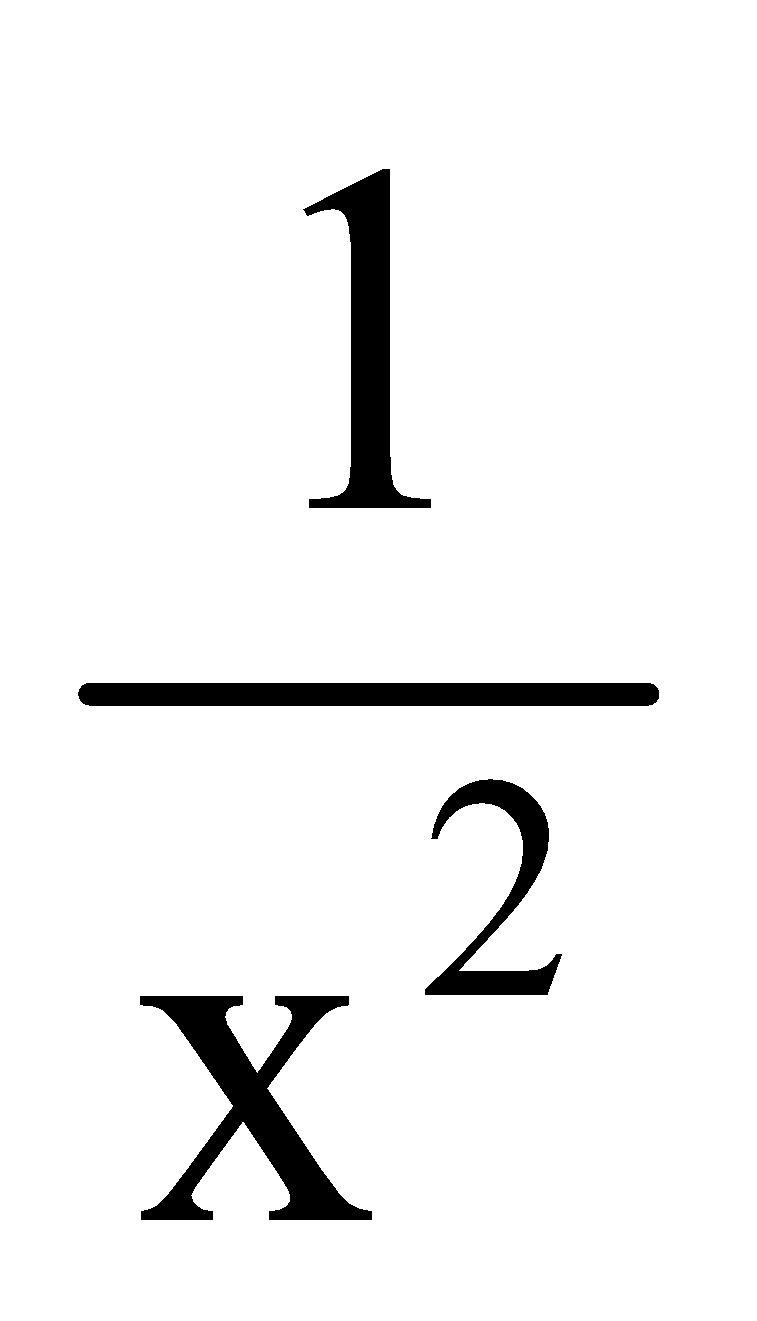 or
or
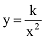
y is proportional to x2 → y ∝
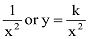
y is proportional to x2 → y ∝ x2 or y = kx2
y is proportional to
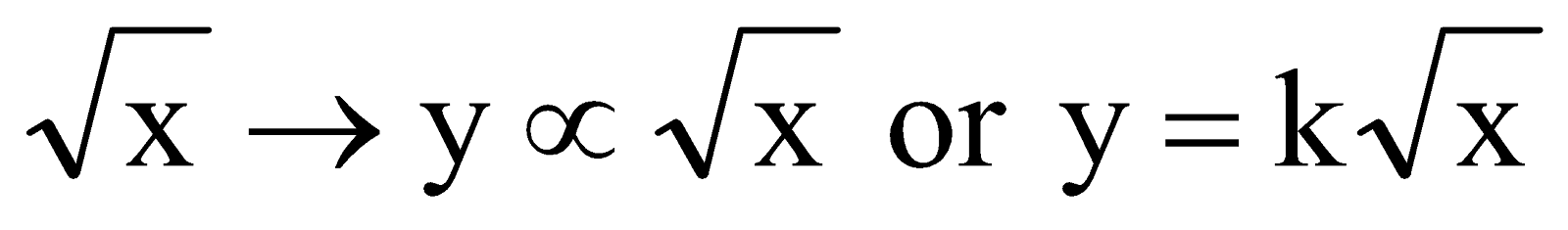
The value of k depends on the actual problem.
It is usually found by solving the equation formed by substituting for given values of x and y.
Also Check







