INVARIANT PROPORTION

Direct and inverse proportions of Class 8

If two quantities are directly proportional then their quotient is an invariant(it does not change, it is constant). Further, if we have another pair of two quantities that are directly proportional then their quotient is also an invariant. Moreover, if you multiple these two quotients, you end up with a third invariant. But, consider the following example.

Given that x is directly proportional to y and to z and is inversely propotional to w, and that x=4 when (w,y,z)=(6,8,5), what is x when (w,y,z)=(4,10,9)?

Correct Solution:

xw is a contant, x/z is a constant, and x/y is a constant.

Thus, xw/yz is constant. (They just combined the constant terms)

so, xw/yz=(4)(6)/(8)(5)=3/5.

Thus, when (w, y, z)=(4,10,9), we find x=3yz / 5w=27/2.

question 1. Jane ran 100 meters in 15 seconds. How long did she take to run 1 meter?

Solution: Step 1: Think of the word problem as:

If 100 then 15. If 1 then how many?

Step 2: Write the proportional relationship:

100 → 15

INVARIANT PROPORTION

She took 0.15 seconds

question 2. If INVARIANT PROPORTION of a tank can be filled in 2 minutes, how many minutes will it take to fill the whole tank?

Solution: Step 1: Think of the word problem as:

If INVARIANT PROPORTION then 2. If 1 then how many? (Whole tank is )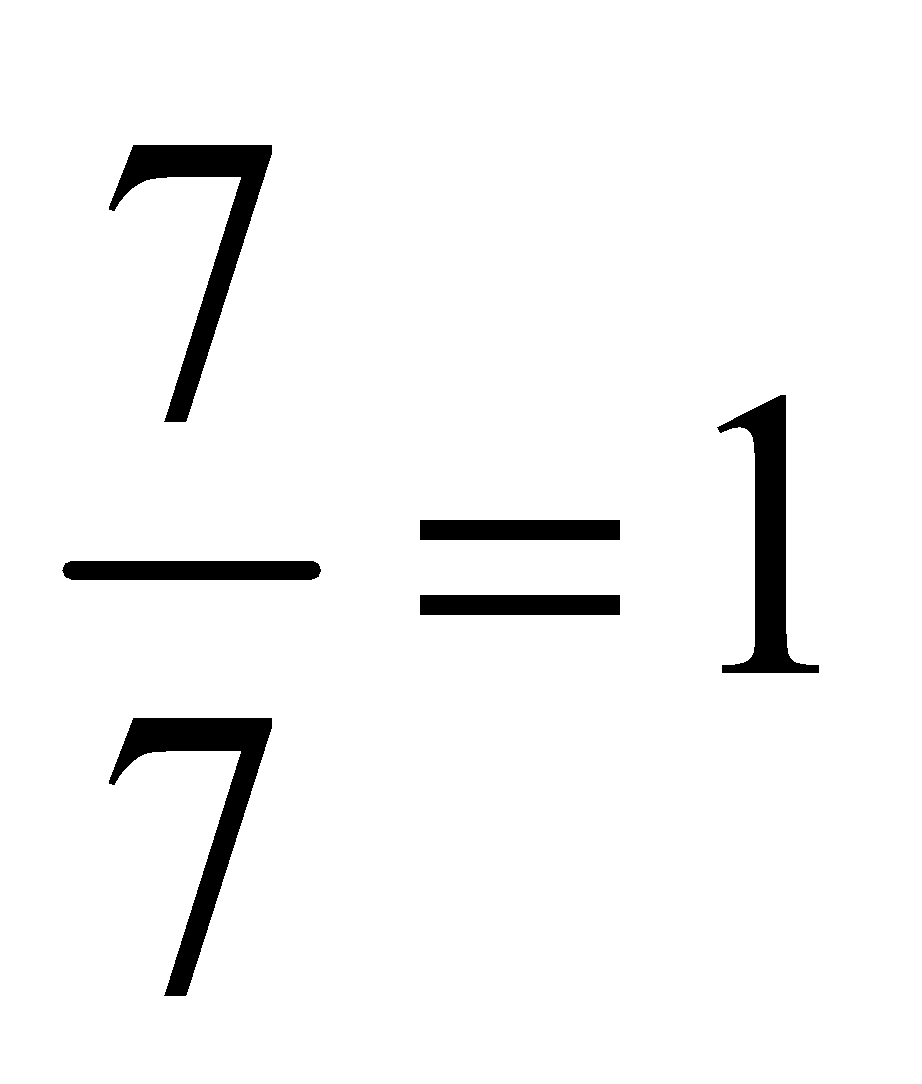

Step 2: Write the proportional relationship:

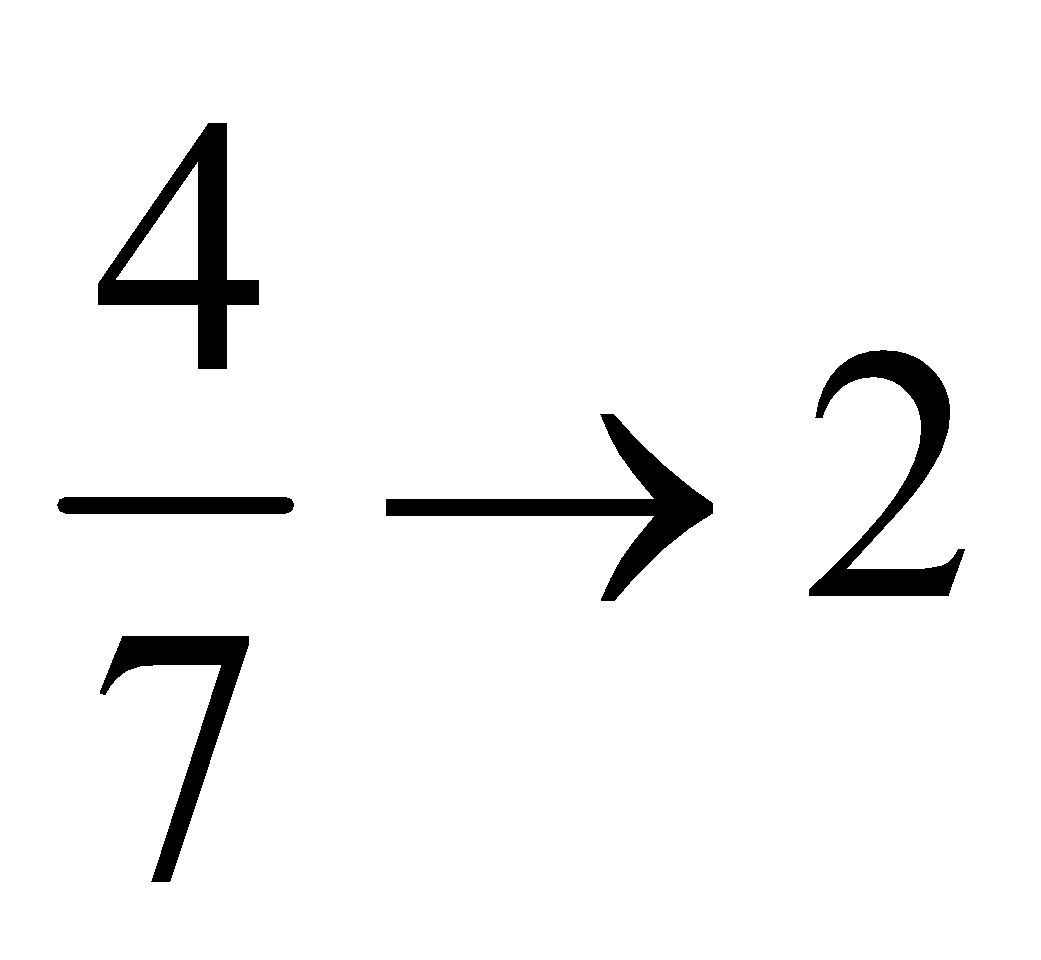
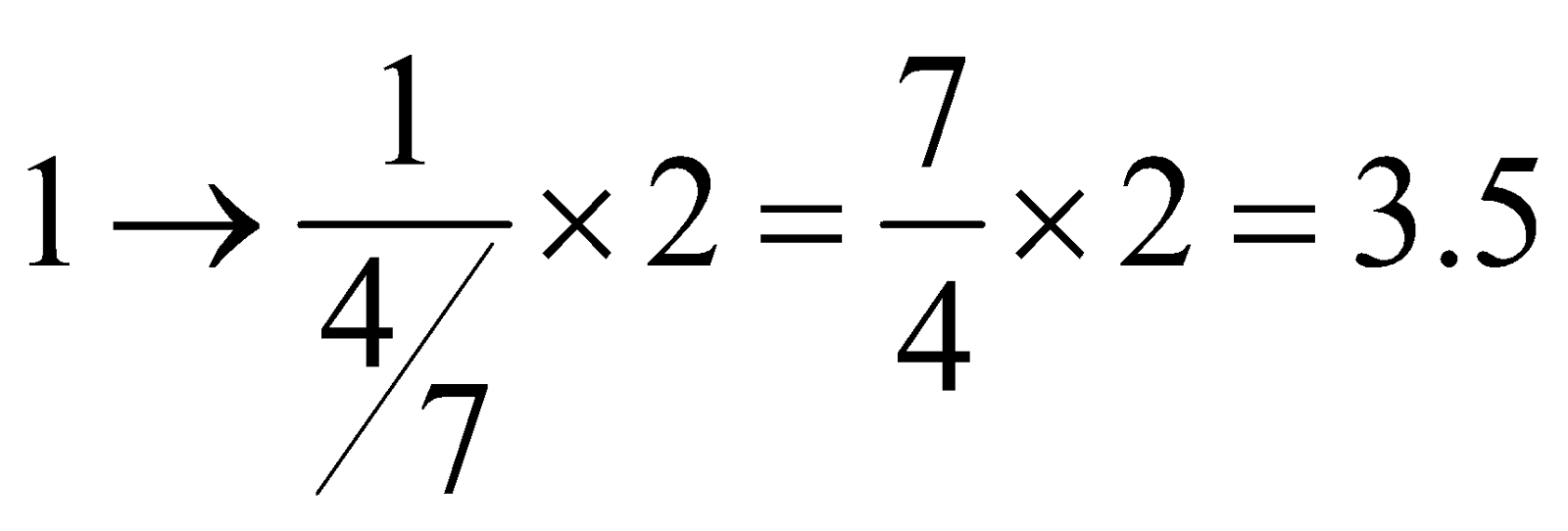
INVARIANT PROPORTION

It took 3.5 minutes

question 3. A car travels 125 miles in 3 hours. How far would it travel in 5 hours?

Solution:Step 1: Think of the word problem as:

If 3 then 125. If 5 then how many?

Step 2: Write the proportional relationship:

3 → 125

INVARIANT PROPORTION

He traveled INVARIANT PROPORTION miles.

e. g. Let the four quantities 3, 4, 9 and 12 be in proportion.

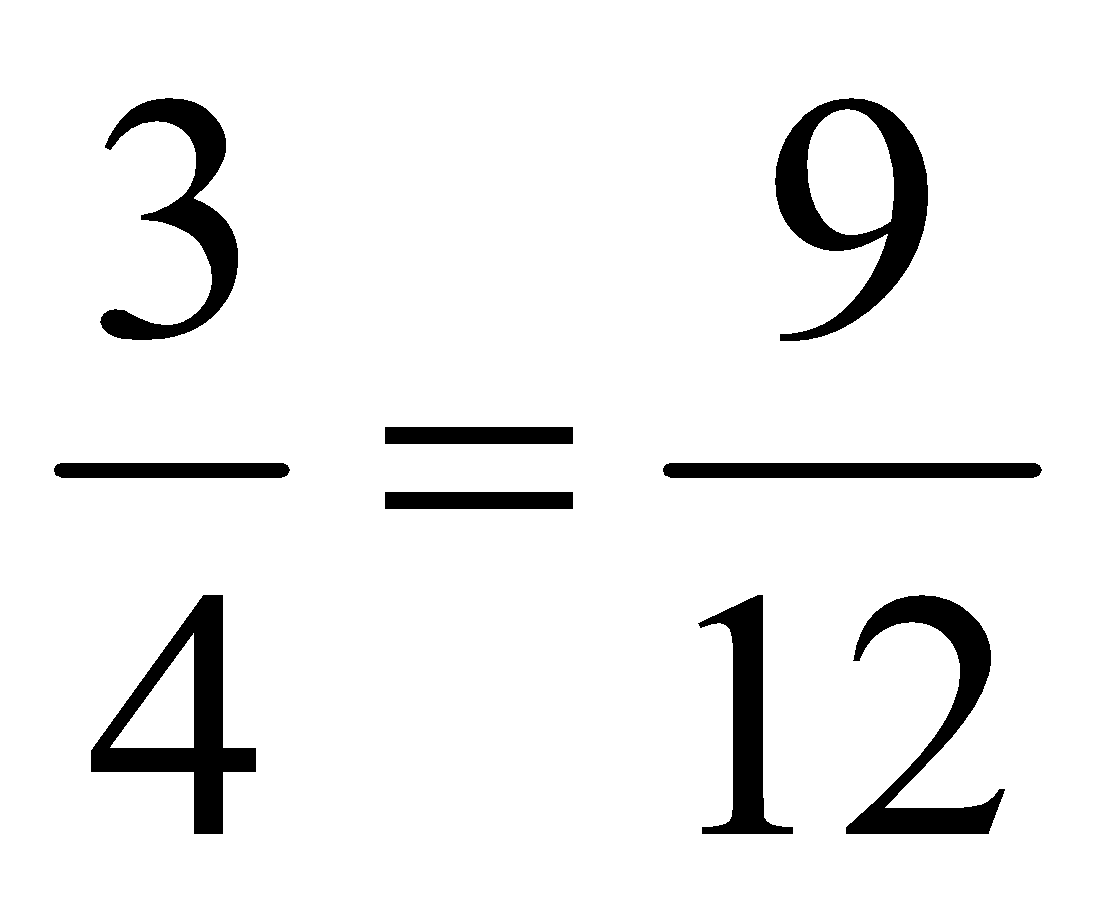INVARIANT PROPORTION or 3 : 4 :: 9 : 12.

These quantities of the same kind are said to be in ‘continued’ proportion when the ratio of the first to the second is equal to the ratio of the second to the third.

The second quantity is called the mean proportional between the first and the third, and the third quantity is called the third proportional to the first and second.

Then 9, 6 and 4 are in continued proportion for 9 : 6 :: 6 : 4.

Hence, 6 is the mean proportional between 9 and 4, and 4 is the third proportional to 9 and 6.

Mean proportion

a : b :: b : c ⇒ b2 = ac

question 4. Find the fourth proportional to the number 6, 8 and 15.

Solution: Let x be fourth proportional

∴ 6 : 8 :: 15 : x

∴ 6 × x = 8 × 15

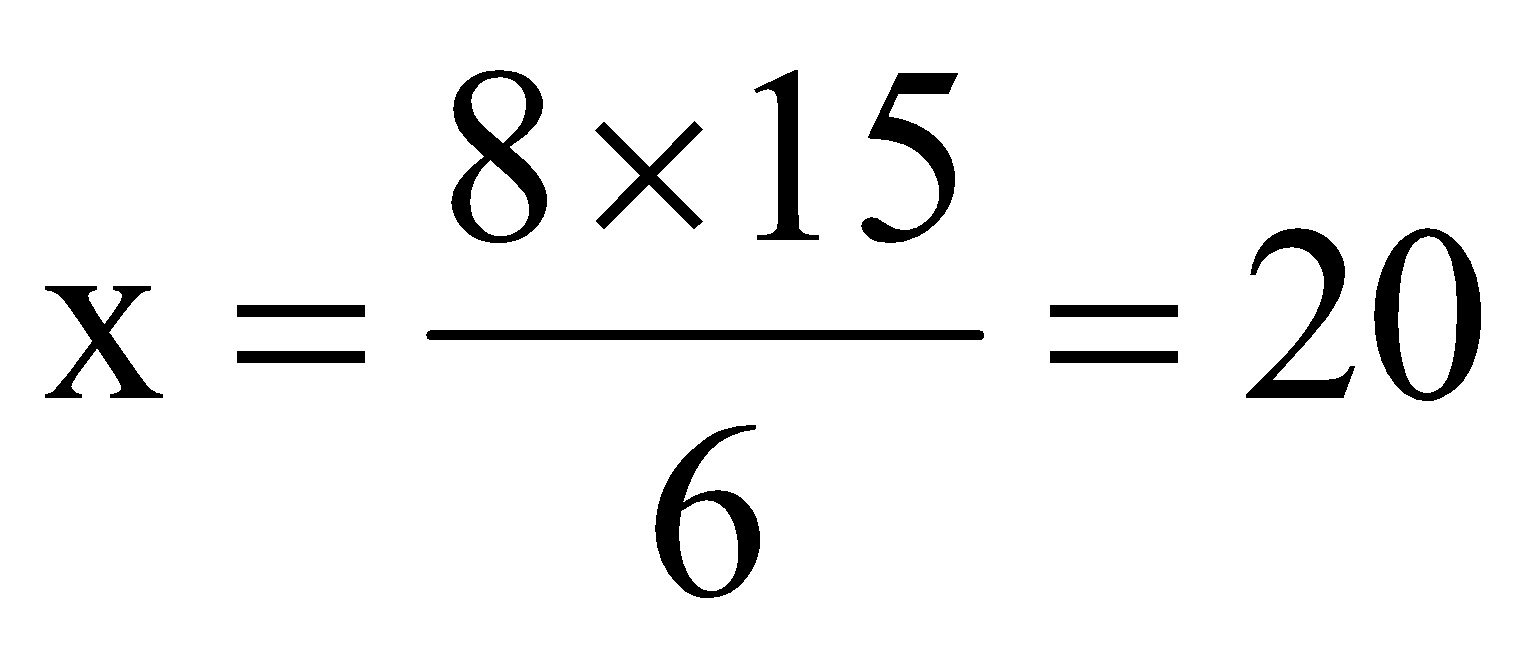
∴ INVARIANT PROPORTION

question 5. Find the third proportional to 15 and 20.

Solution: Here, we have to find a fourth proportional to 15, 20 and 20.

( INVARIANT PROPORTION it is continued proportion).

Let x be the fourth proportional.

We have 15 : 20 :: 20 : x

15 × x = 20 × 20

∴ x = INVARIANT PROPORTION

question 6. Find the mean proportional between 3 and 75.

Solution: Let x be the required mean proportion.

3 : x :: x : 75

∴ x2 = 3 × 75

x2 = 225

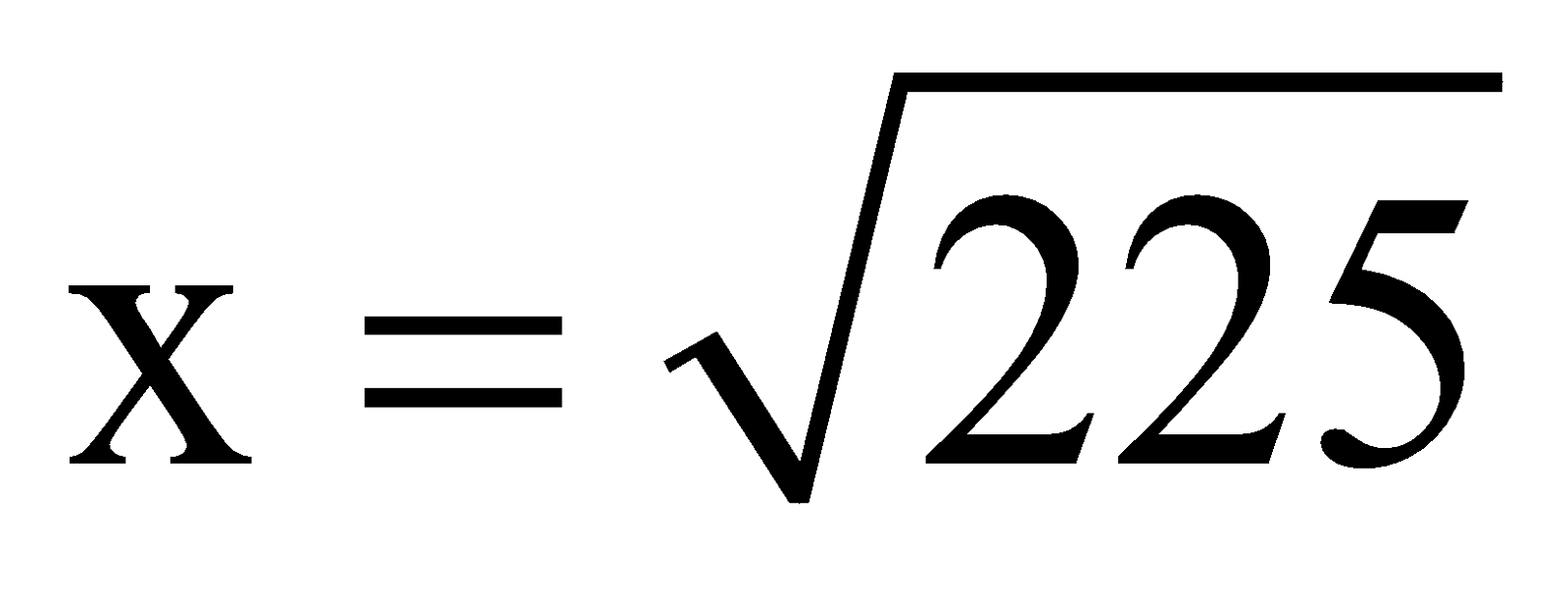
∴ INVARIANT PROPORTION

x = 15

DIRECT PROPORTION (DIRECT VARIATION):

The cost of articles varies directly as number of articles.
The distance covered by a moving object varies directly as its speed.
The work done varies directly as the number of men at work.

Rule: Two quantities a and b are in direct variation, the ratio of any two values of a is equal to the ratio of the corresponding values of b.

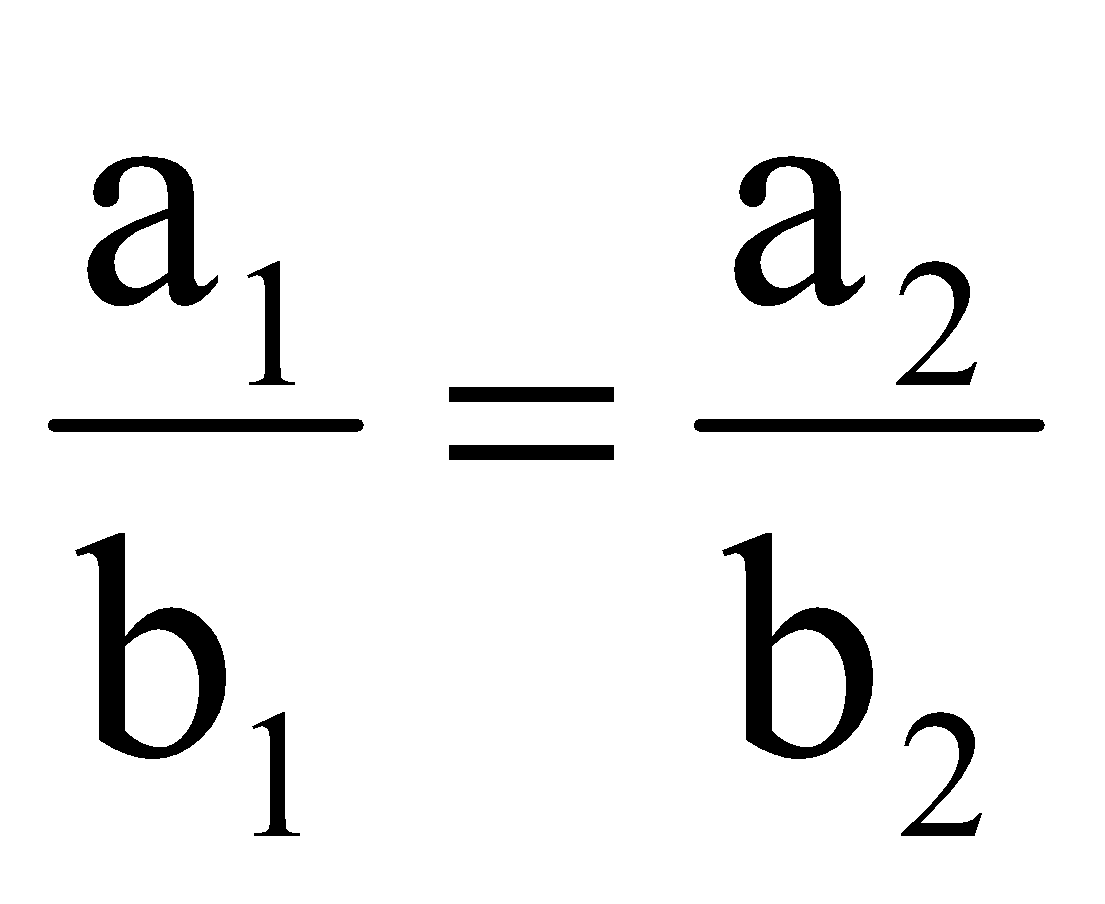
INVARIANT PROPORTION

∴ a1b2 = a2b1 ⇒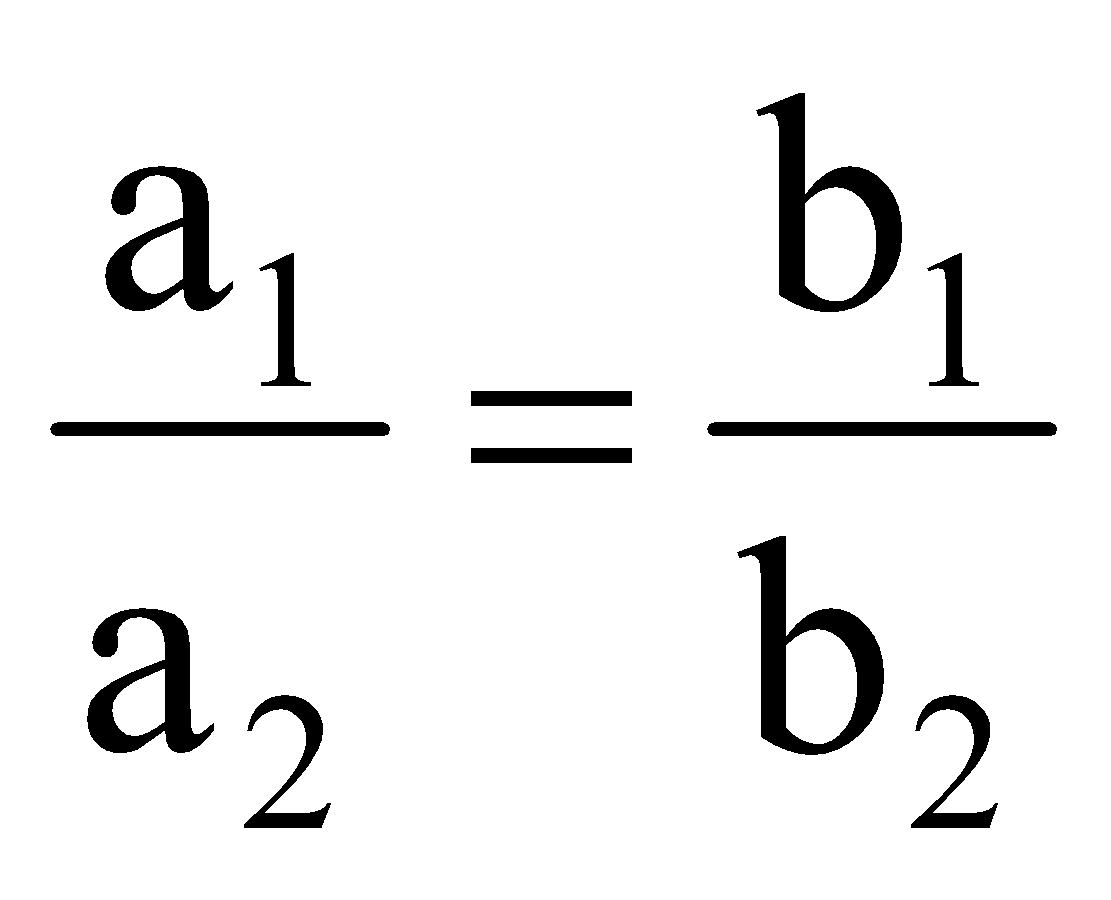

∴ a1 : a2 :: b1 : b2

question 1. If one score oranges cost Rs. 45, how many oranges can be brought for Rs. 72?

Solution: For Rs. 45, number of oranges brought = 20

For Rs. 1 number of oranges brought = 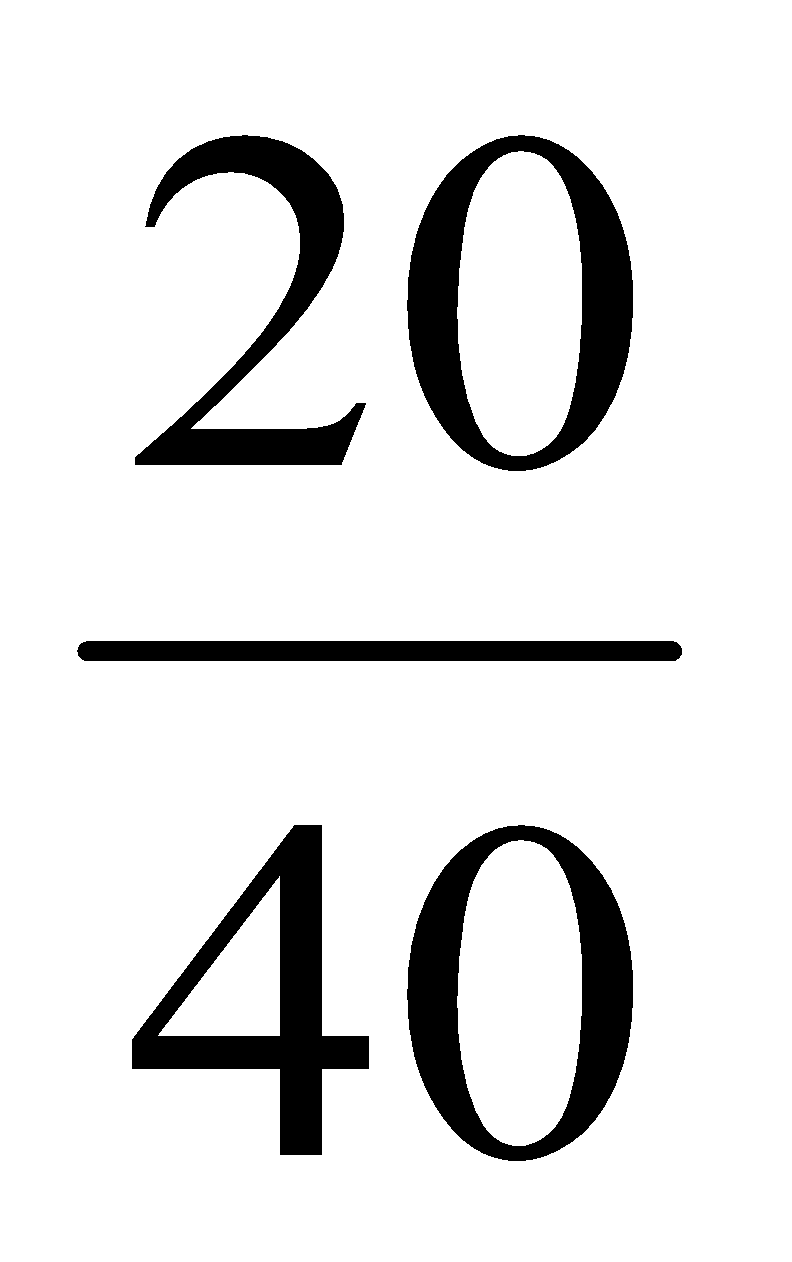INVARIANT PROPORTION

For Rs. 72 number of oranges brought = INVARIANT PROPORTION

Number of oranges = 32

question 2. A taxi charges a fare of Rs. 260 for a journey of 200 km. How much would it travel for Rs.279.50.

Solution: But taxi travels x km for Rs. 279.50.

Fare (Rs.)	260	279.50
Distance (km)	200	x

∴ Ratio of Rs = Ratio of distance

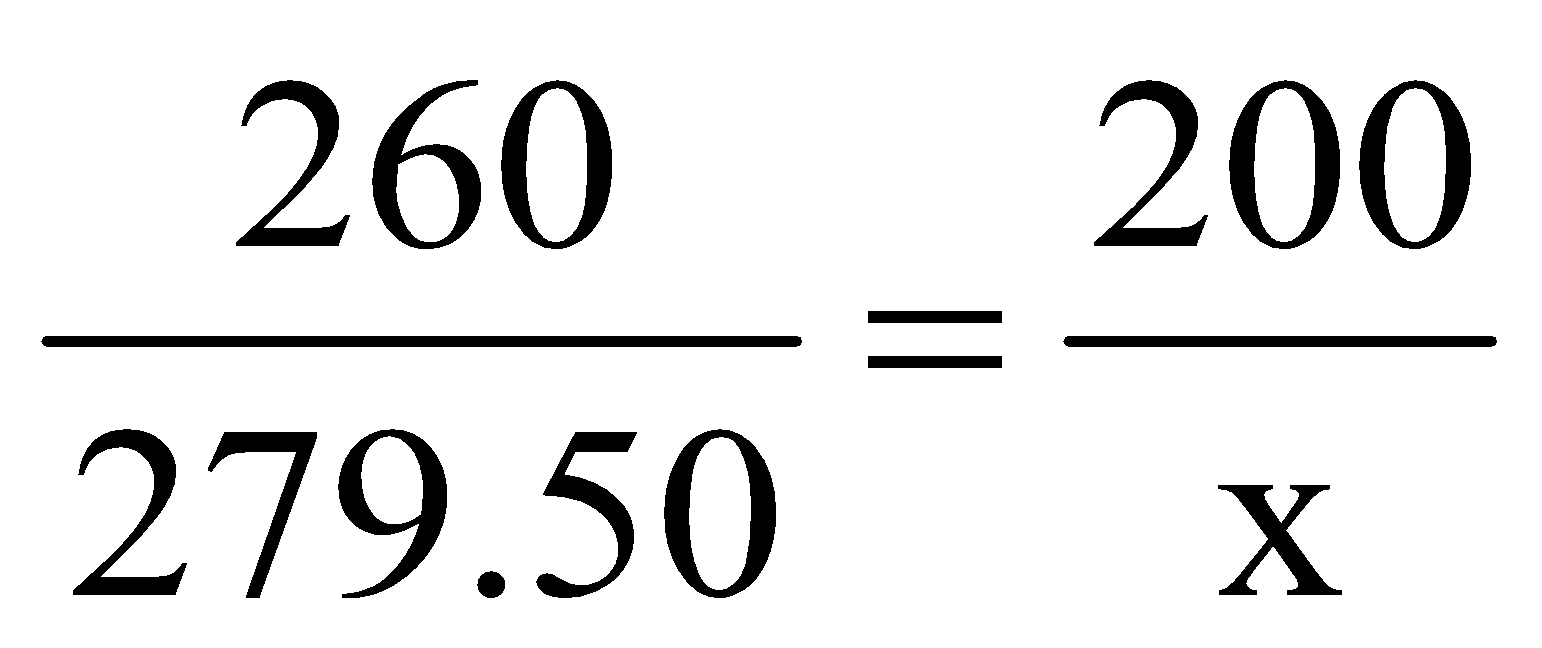
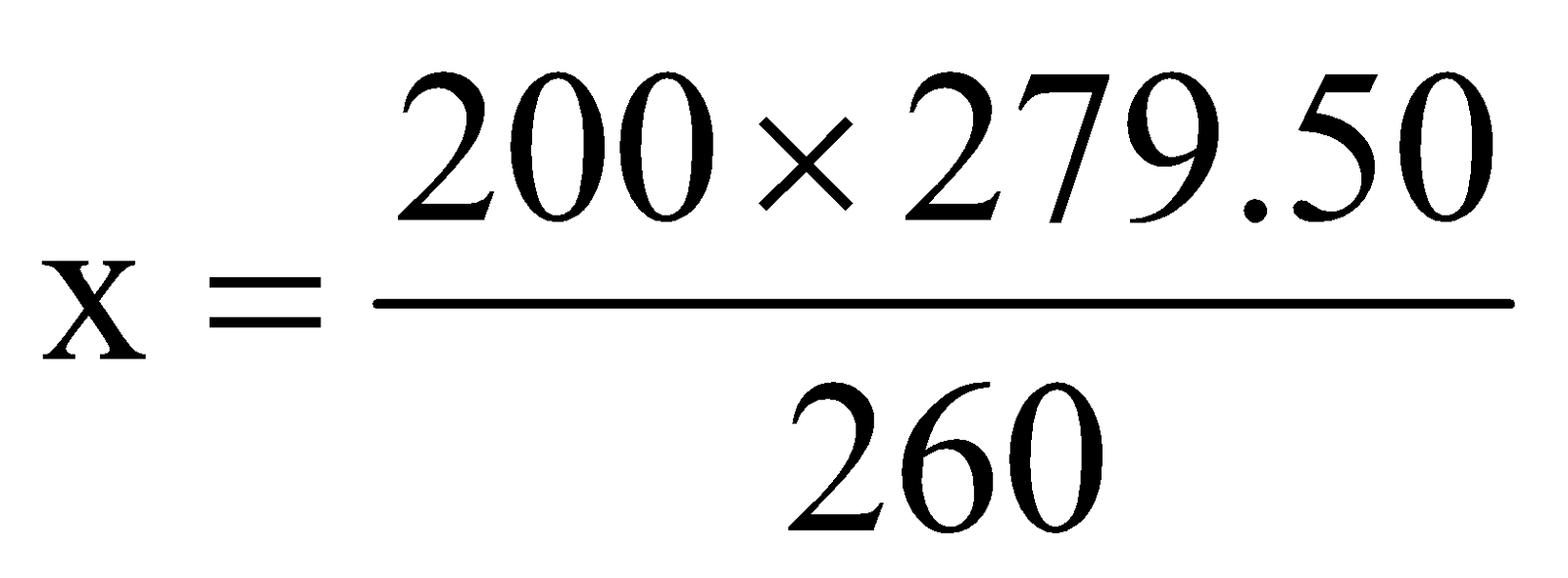
INVARIANT PROPORTION

⇒ x = 215

The taxi will come 215 km

question 3. If 3 men and 4 women earn Rs. 480 in a day. Find how much will 7 men and 11 women earn in a day?

Solution: Let men will earn x Rs.

Women will earn y Rs.

For men

Men	3	7
Rs.	480	x

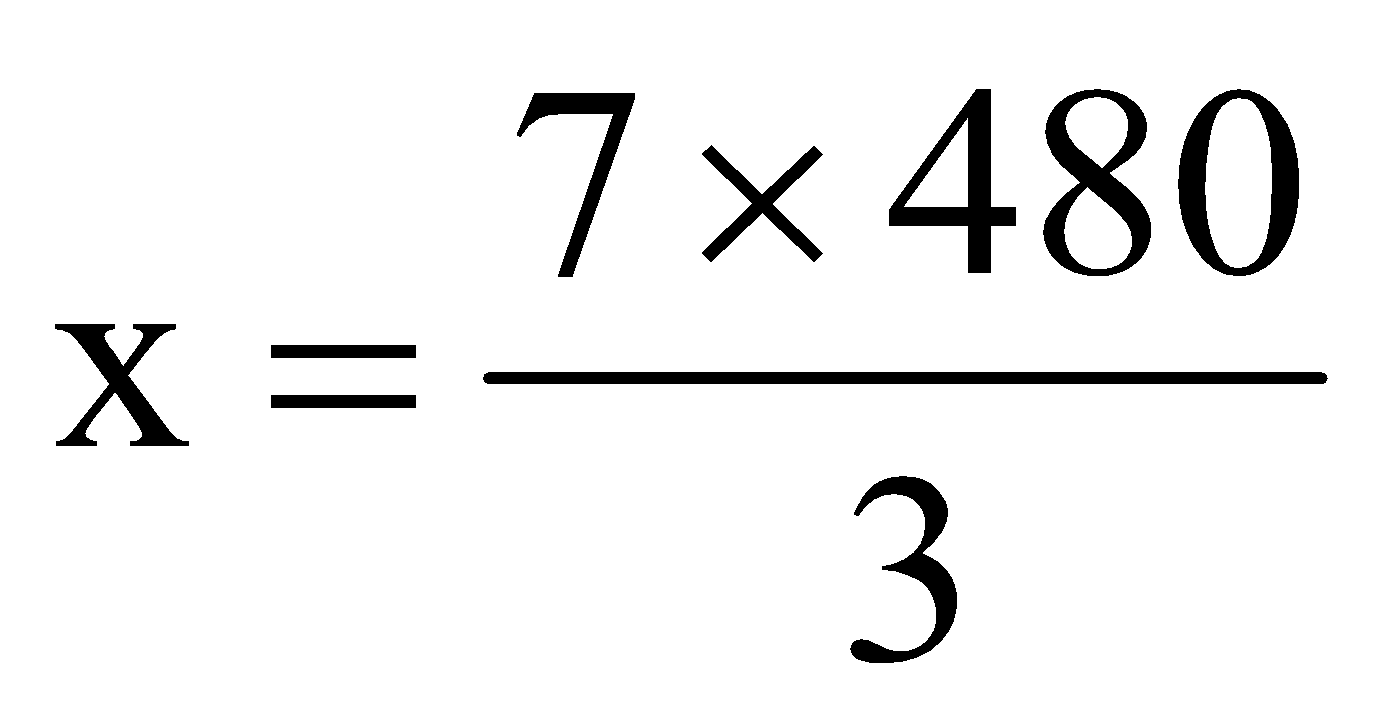
INVARIANT PROPORTION

x = 1120

Men will earn Rs. 1120 (1)

For women

Women	4	11
Rs.	480	y

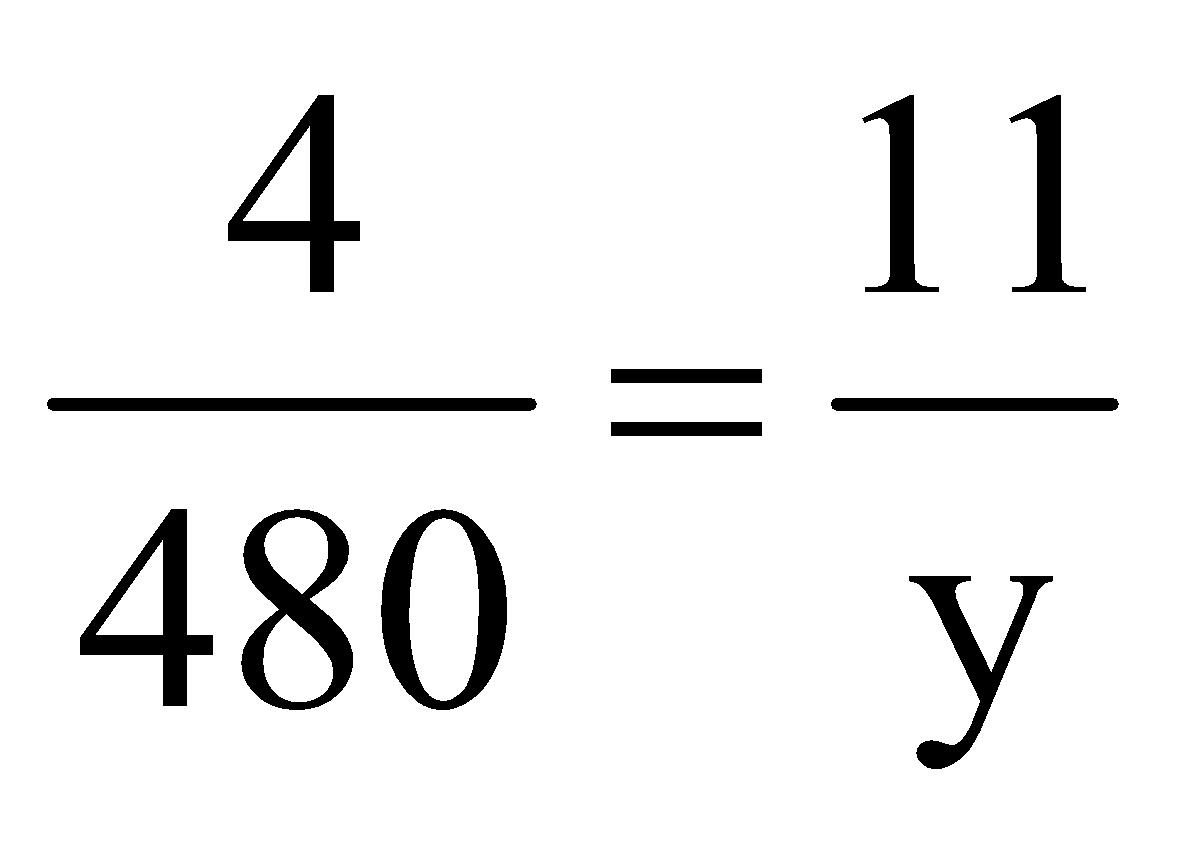
⇒ INVARIANT PROPORTION

∴ INVARIANT PROPORTION

y = 1320

Women will earn Rs. 1320.

Total money for 7 men and 11 women in day

= 1120 + 1320 = 2440

i.e. Rs. 2440

question 4. If the wages of 15 workers for 6 days are Rs. 9450. Find the wages of 19 workers for 5 days.

Solution:Let the wages be x.

First find relation between wages and workers.

Workers	15	19
Wages	9450	x

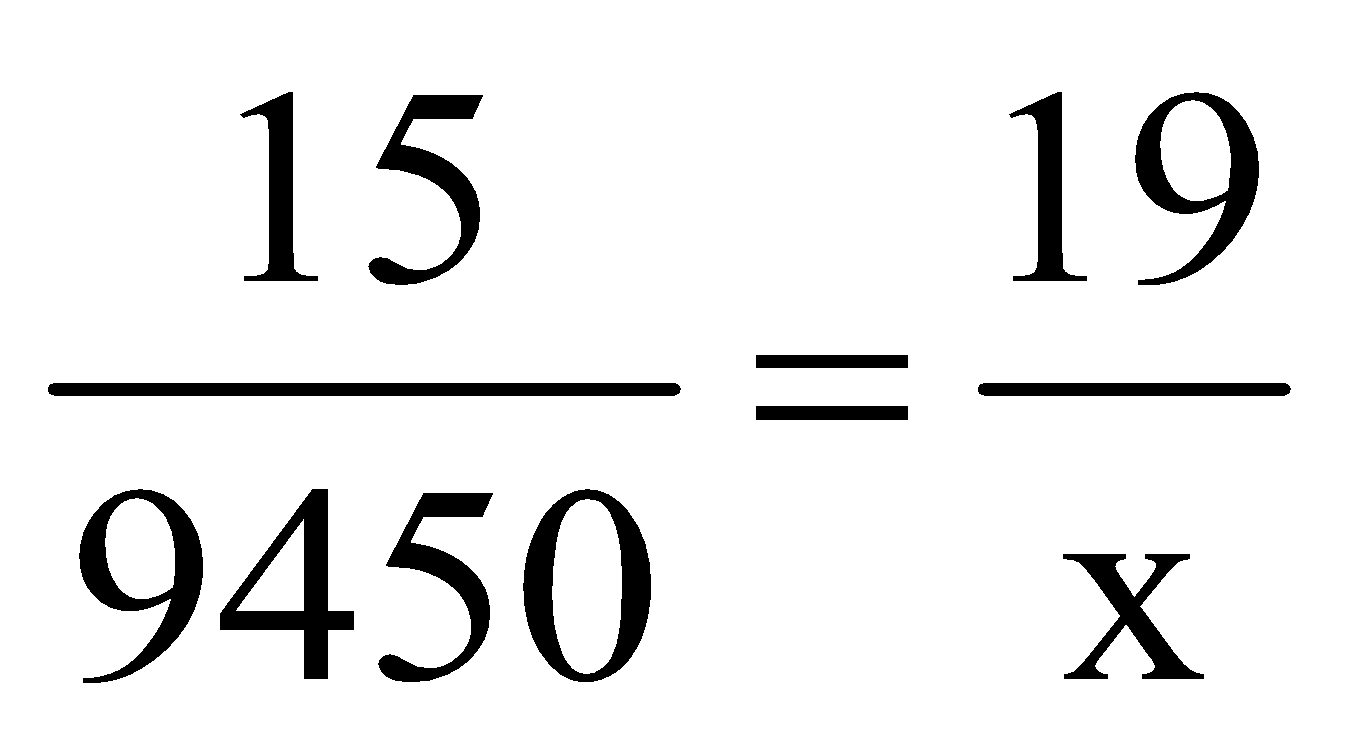
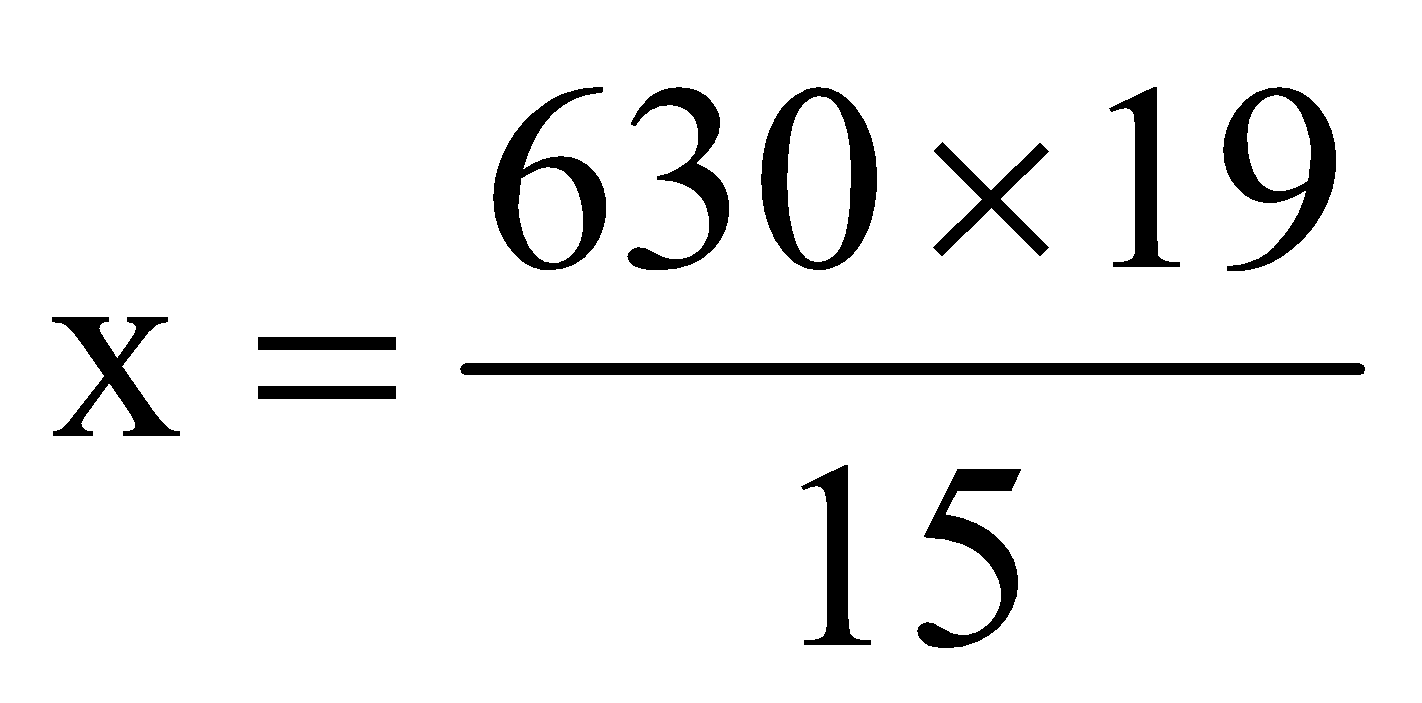
∴ INVARIANT PROPORTION

x = Rs. 11970

Now ratio between days wages

Days	6	5
Wages	11970	y

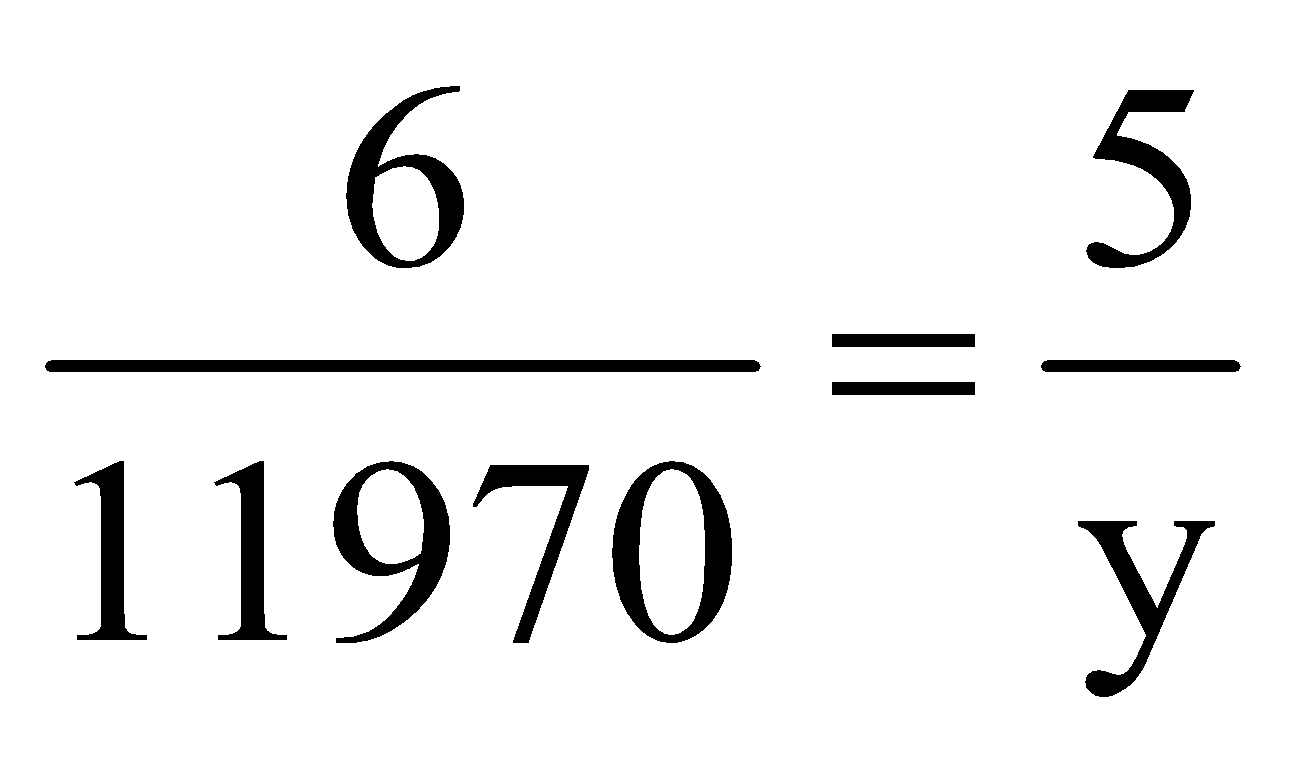
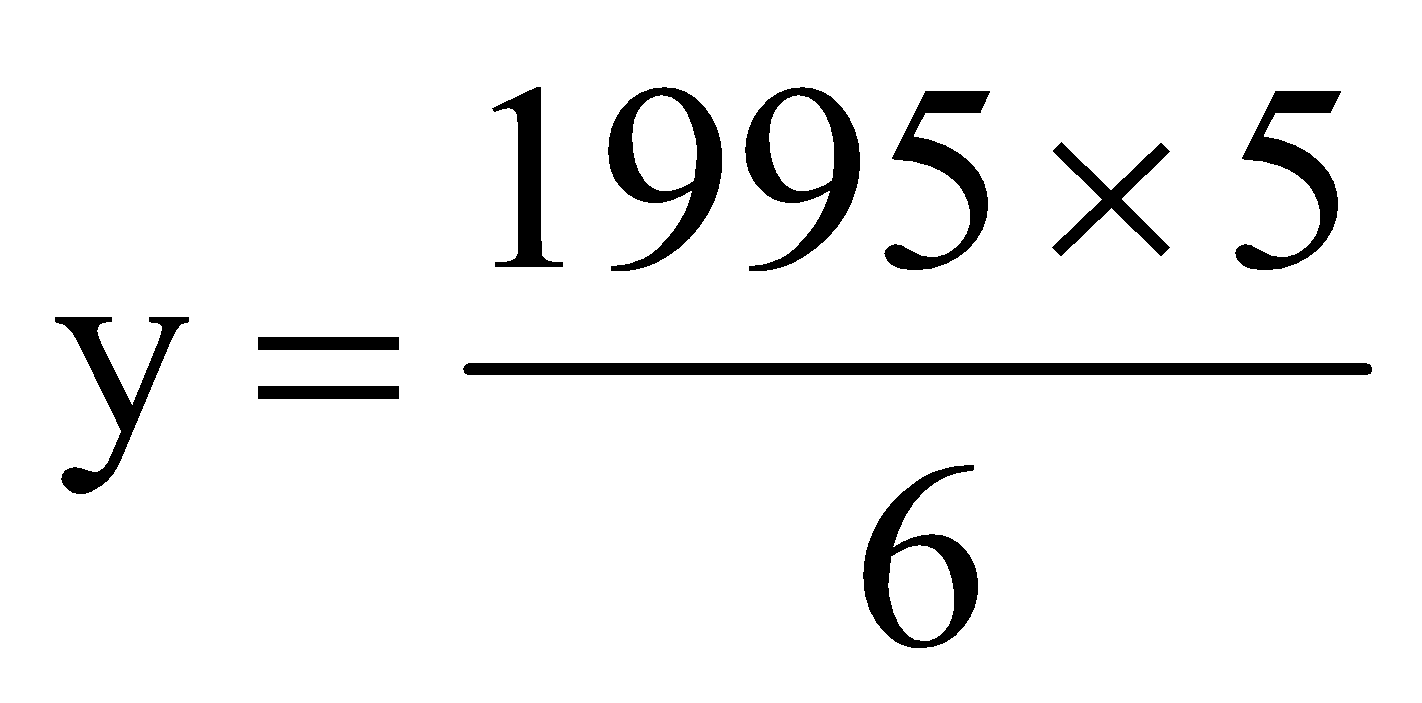
⇒ INVARIANT PROPORTION

y = Rs. 9975

Hence the wages of 19 workers for 5 day = Rs. 9975.

5. The cost of 16 packets of salt, each weighing 900 grams is Rs. 84. What will be the cost of 27 packets of salt, each weighing 1 kg?

Solution: Cost of 16 packets each weighing INVARIANT PROPORTION kg = Rs. 84

Cost of 16 packets, each weighing 1 kg = Rs. INVARIANT PROPORTION

Cost of 1 packet, each weighing 1 kg = Rs. 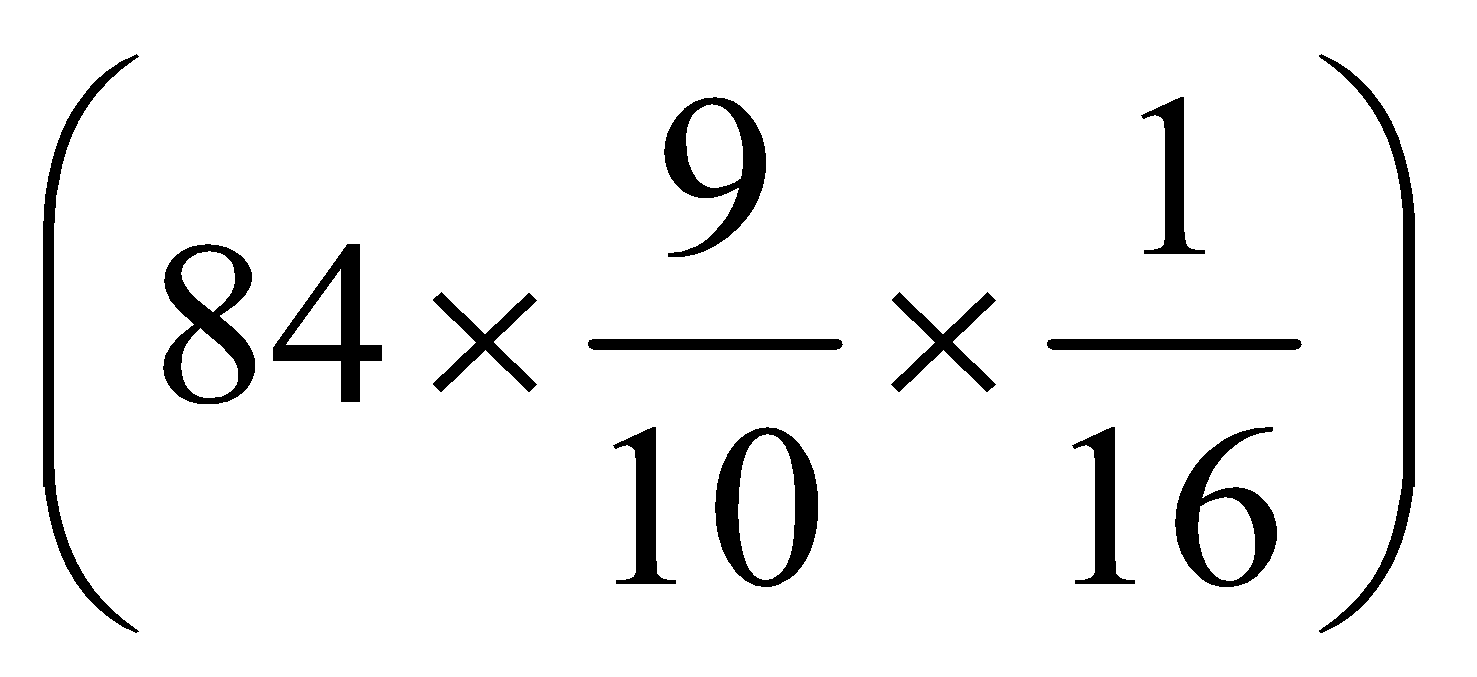INVARIANT PROPORTION

Cost of 27 packets, each weighing 1 kg = Rs. 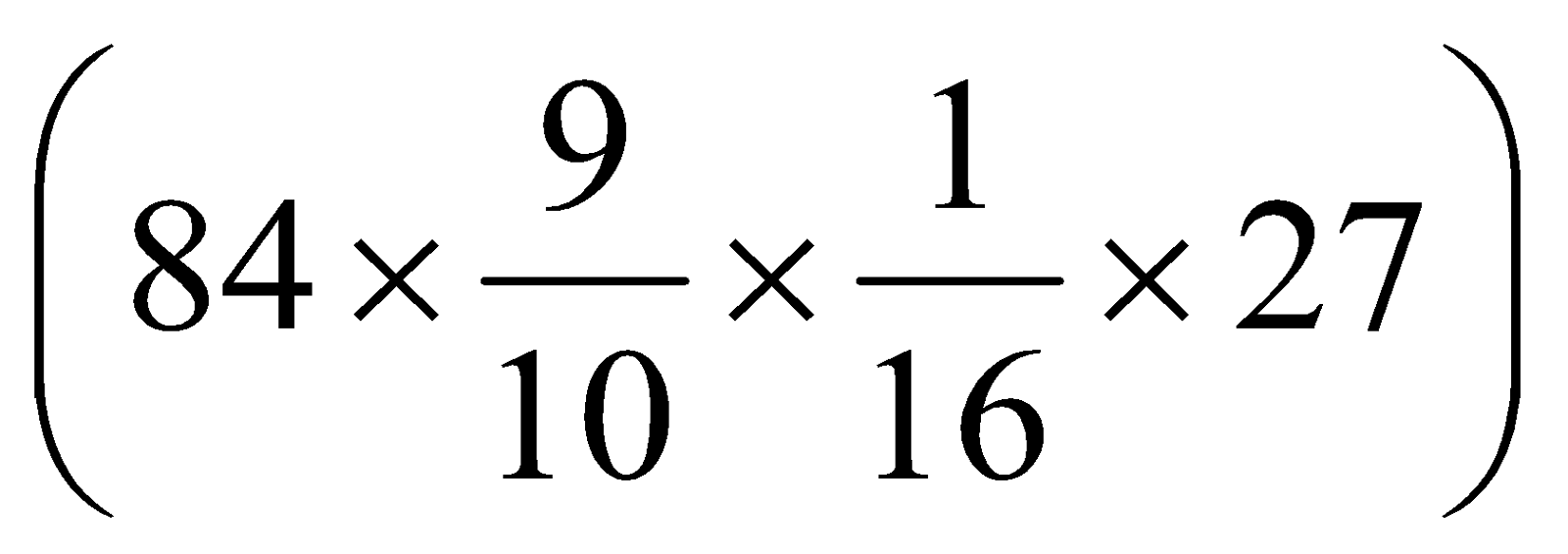INVARIANT PROPORTION

= Rs. INVARIANT PROPORTION = Rs. 157.50

Hence the cost of 27 packets, each weighing 1 kg is Rs. 157.50

INVERSE PROPORTION (INVERSE VARIATION):

Inversely Proportional questions are similar to directly proportional problems, but the difference is that when x increase y will decrease and vice versa – which is the inverse proportion relationship. The most common example of inverse proportion problems would be “the more men on a job the less time taken for the job to complete”

Again, the technique is to change the proportion problems into the form:

If x then y. If x is changed to a then what will be the value of y?

and then write the inverse relationship (take note of the "inverse" form):

x → y

(i) The time taken to finish a piece of work varies inversely as the number of men at work.

(ii) The speed varies inversely as the time taken to cover a distance.

Rule: If two quantities a and b vary inversely as each other, and b1, b2 are the values if b corresponding to the values a1, a2 of a respectively, then

a1b1 = k and a2b2 = k

∴ a1b1 = a2b2

⇒ a1 : a2 = b1 : b2 or a1 : a2 :: b1 : b2