Combination of Resistors

Many times we have to join two or more resistances to get the desirable resistance. There are two ways in which resistances be joined:

1. Resistances in series
2. Resistances in Parallel

Resistance in Series

A number of resistances are said to be connected in series if they are joined end to end and the same current flows through each one of them, when a potential difference is applied across the combination.

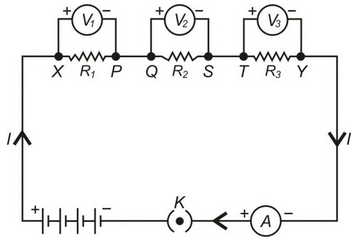
R ₁ , R ₂ , R ₃ – Resistances in series.

V – Total potential difference across XY.

V ₁ , V ₂ , V ₃ – Potential difference across R ₁ , R ₂ , R ₃ respectively.

I – Current flowing through combination.

So, V = V ₁ + V ₂ + V ₃ ... (i) [Potential difference gets divided among

resistances joined in series]

According to Ohm's Law:

V ₁ = IR ₁ ... (ii)

V ₂ = IR ₂ ... (iii)

V ₃ = IR ₃ ... (iv)

Let R is the resultant or equivalent resistance of the combination. Then

V = IR ... (v)

From (i), (ii), (iii), (iv) and (v) we get that:

IR = IR ₁ + IR ₂ + IR ₃

IR = I(R ₁ + R ₂ + R ₃ )

R = R ₁ + R ₂ + R3

THINGS TO REMEMBER IN SERIES CONNECTION:

1. When a number of resistances are connected in series, the equivalent or resultant resistance is equal to the sum of individual resistances and resultant resistance is greater than any individual resistance.

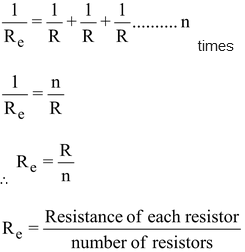
2. If n resistances each of value R are connected in series, the equivalent resistance Re is given by:

Re = R + R + R .......... n times

Re = nR

Re = Number of resistors × resistance of each resistor

3. Equal current flows through each resistance and it is also equal to the total current in the circuit. This is because there is no other path along which the current can flow.

4. The potential difference across the ends of the combination is distributed across the ends of each of the resistances. The potential difference across any one of the resistances is directly proportional to its resistance.

5. The equivalent resistance when used in place of the combination of resistances produces the same current with the same potential difference applied across its ends.

6. When two or more resistances are joined in series, the result is the same as increasing the length of the conductor. In both cases the resultant resistance is higher.

7. In a series combination, the equivalent resistance is greater than the greatest resistance in the combination.

RESISTANCES IN PARALLEL:

A number of resistors are said to be in a parallel connection if one end of each resistance is connected to one point and the other is connected to another point. The potential difference across each resistor is the same and is equal to the applied potential difference between the two points.

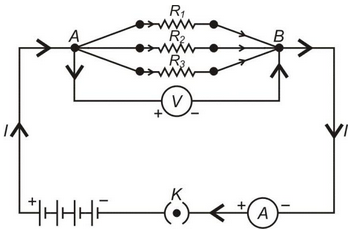
R ₁ , R ₂ , R ₃ – Three resistances in parallel connection.

V – Potential difference across A and B.

I – Total current flowing between A and B.

I ₁ , I ₂ , I ₃ – Current flowing through R ₁ , R _2, R ₃ respectively.

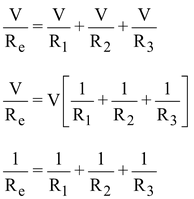
I = I ₁ + I ₂ + I ₃ ... (i) [In parallel connection, the current gets divided among the resistances]

The potential difference across R ₁ , R ₂ and R ₃ is same, therefore, according to Ohm's law:

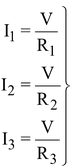... (ii)

Let Re be the equivalent resistance. Thus

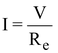... (iii)

From equation (i), (ii) and (iii) we get

THINGS TO REMEMBER IN PARALLEL CONNECTION:

• When a number of resistances are connected in parallel, the reciprocal of the equivalent or resultant resistance is equal to the sum of reciprocals of the individual resistances and is always smaller than the individual resistances. This is because there are a number of paths for the flow of electrons.
• If there are n resistances connected in parallel and each resistance has a value of R

• The potential difference across each resistance is the same and is equal to the total potential difference across the combination.
• The total current divides itself and different current flows through each resistor. The maximum current flows through the resistor having minimum resistance and vice versa.
• If an equivalent resistance Re is connected in place of combination, it produces the same current for the same potential difference applied across its ends.
• In a parallel combination, the equivalent resistance is lesser than the least of all the resistances.
• If two resistances R ₁ and R ₂ are connected in parallel then

• If there are n resistors each of resistance R – Let RS be the resultant resistance of series combination and Rp be the resultant resistance of parallel combination.

Then, RS = nR

Rp = R/n

∴

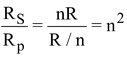
HEATING EFFECT OF ELECTRIC CURRENT:

When the ends of a conductor are connected to a battery, then free electrons move with drift velocity and electric current flows through the wire. These electrons collide continuously with the positive ions of the wire and thus the energy taken from the battery is dissipated. To maintain the electric current in the wire, energy is taken continuously from the battery. This energy is transferred to the ions of the wire by the electrons. This increases the thermal motion of the ions, as a result the temperature of the wire rises. The effect of electric current due to which heat is produced in a wire when current is passed through it is called heating effect of current or Joule heating. In 1841 Joule found that when current is passed through a conductor the heat produced across it is:

1. Directly proportional to the square of the current through the conductor i.e. H ∝ I 2
2. Directly proportional to the resistance of the conductor i.e. H ∝ R
3. Directly proportional to the time for which the current is passed i.e. H ∝ t
4. Combining the above three equations we have H ∝ I 2 Rt

Where J is called Joule's mechanical equivalent of heat and has a value of J = 4.18 J cal -1 . The above equation is called Joule's law of heating.

In some cases, heating is desirable, while in many cases, such as electric motors, generators or transformers, it is highly undesirable. Some of the devices in which heating effect of an electric current is desirable, are incandescent lamps, toasters, electric irons and stoves. The tungsten filament of an incandescent lamp operates at a temperature of 2700°C. Here, we see electrical energy being converted into both heat and light energy.