Types Of Half Cells
Share
Types Of Half Cells
Electrochemistry of Class 12
Types Of Half Cells
Gas Electrodes
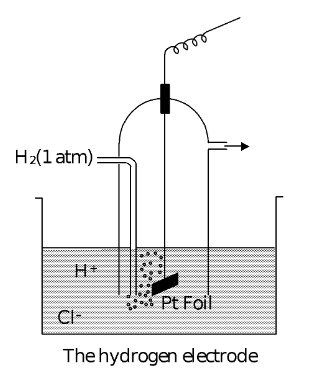
(1) Hydrogen Electrode
Hydrogen gas bubbling in a solution of an acid (say, HCl) forms an electrode of this type. Since hydrogen gas is non-conducting, platinum or some other metal, which is not attacked by the acid and easily comes into
equilibrium
with hydrogen, is used for making electrical
contact in the circuit.
|
The electrode is prepared electrochemically by depositing platinum on platinum metal. This gives a large surface area for the adsorption of gases. Thermochemical studies shows that hydrogen is adsorbed on platinum in atomic state. The reactions are
½H
2
(g)
H(Pt)
The net reaction is
½H
2
(g)
The electrode assembly is represented as (if the half cell is acting as cathode)
|
|
(2) Chlorine Electrode
In this electrode, chlorine gas at a given pressure is bubbled into a solution of HCl. The electrode acting as cathode is represented as
Cl−(aq)⏐Cl 2 (g)⏐Pt
and the electrode reaction is written as
½ Cl
2
(g) + e−
Cl−(aq)
(3) Oxygen Electrode
In this electrode, oxygen gas at a given pressure is bubbled through a solution containing hydroxyl OH− ions. The electrode reaction is written as
O
2
(g) + 2H
2
O + 4e−
4OH−(aq)
The electrode acting as cathode is represented as (aq)OH−⏐O 2 (g)⏐Pt
Metal−Metal Ion Electrodes
The electrodes used in the Daniel cell are the examples of metal−metal ion electrodes. Another example of this type is a silver−silver ion electrode which is represented as Ag |
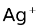. The anodic half−cell reaction is
Ag(s)
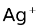(aq) + e−
[Note: Very active metals reacts directly with water and thus cannot be used for such electrodes]
A metal electrode may be made of an amalgam of the metal in mercury instead of the pure metal. Some of the irreproducible effects associated with solid surfaces are eliminated when amalgam electrodes are used. Amalgams offer the only route for the study of the electrochemistry of highly reactive metals in this pure state.
Redox Electrodes
A redox electrode consists of ions of two different oxidation states and a non−reactive metal, usually platinum. An example is Pt |
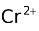(c
1
),
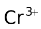(c
2
). The half cell reaction with this electrode as the anode is
.
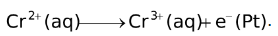Redox electrode can also be made with organic molecules that can exist in two different oxidation states. A biochemical system of hydroquinone(QH2) and quinone(Q) forms a redox electrode which is abbreviated as (for anode)
Pt | QH
2
, Q,
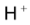
The half cell reaction is represented as
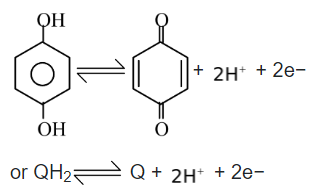
This electrode is called quinhydrone electrode because of the charged complex formed between quinone and hydroquinone.
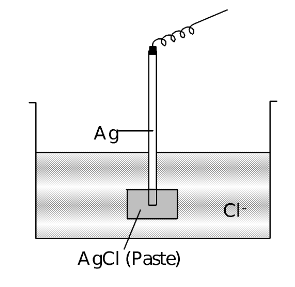
Metal-Insoluble Metal Salt −Anion Electrodes
An example of this type of electrode is Cl−⏐AgCl⏐Ag. In this electrode a solution of Cl− is taken and a rod of Ag coated with a paste of AgCl is dipped into this solution. The reaction that take place are:
AgCl
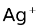+ Cl−…(i)
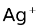+ e−→ Ag …(ii)
Net half reaction: AgCl + e−→ Ag + Cl−…(iii)
|
These electrodes are constructed for any metal with its insoluble metal salt dipped in a solution containing the common anion of the salt and not the common cation (obviously the anion in the solution should come from highly soluble electrolyte). Moreover, the cation in the solution should have a standard reduction potential less than that of the electrode under consideration . |
|
To understand the given electrode better, we would solve a problem by two different methods.
Example 5
Calculate the half cell potential of Cl−(c
1
)⏐AgCl⏐Ag electrode. Given the value of E° for Ag+ + e–
Ag and Ksp of AgCl.
Solution
Method – I
Let us first understand what is given and what is asked.
Given : Concentration of Cl– as c1
AgCl
Ag+ + Cl–…(i) KSP
Ag+ + e−
Ag…(ii) E°
Asked: E for AgCl + e–
Ag + Cl–…(iii)
We can see that the ΔG1, for the reaction (i) is zero as it is in equilibrium. ΔG 2 for the second reaction is –nFE while for the third reaction is –nFE′. Since ΔG is a thermodynamic quantity, it will follow the Hess’s law, according to which all thermodynamic quantities can be treated in the same manner as we treat the reaction. That is to say if reaction (iii) = (i) + (ii) then ΔG3 = ΔG 1 + ΔG 2.
ΔG
1
is zero, ΔG
3
= ΔG
2
. This implies that –nFE′ = –nFE. n is equal for reaction
(ii) and (iii).
∴ E′ = E
This means that the half cell potential of the third reaction is equal to that of the second one. Now to calculate the half cell potential of the second reaction,
Ag+ + e–→ Ag, we need its E° and concentration of Ag+
E° is given and [Ag+] can be calculated as
∴
Method- II
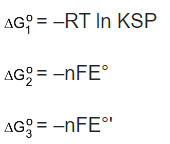
According to Hess’s law,
–nFE°′ = –RT ln KSP –nFE°
Using this equation, we can calculate the E°′ of the reaction (iii). Since we are given the [Cl−] as c1, we can use the half cell potential expression of the reaction (iii) which is,
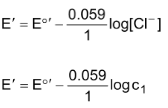
Note: Can we replace the half cell
(c1) Cl−⏐AgCl⏐Ag by Ag+ (KSP/c1) | Ag in half cells ?
(KSP)
The answer is yes, provided you want to calculate the emf of the cell. This is because the emf of the first half cell is given by
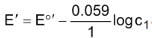and we have already proved that this is equal to the emf of the other half cell.
Another metal−insoluble salt−anion electrode is the calomel electrode which is used as a reference electrode. The calomel electrode is represented as Cl−(c) | Hg2Cl2 | Hg. The cathodic half cell reaction is ½Hg
2
Cl
2
(s) + e−
Hg(l) + Cl−(aq)
