

Thermodynamics Formula is a subfield of physics that studies the interactions between internal energy, work, and heat transmission. In thermodynamics, the system is defined as a quantity of matter or a system in space under observation. The environment, often known as the surroundings, is everything outside of the system. The boundary line is the theoretical or physical line dividing the system from its surroundings.
Zeroth Law of Thermodynamics
As per Zeroth law of Thermodynamics, if two thermodynamic systems are in thermal equilibrium with the third system, then all three systems are in thermal equilibrium with each other. We can take the example of the thermometer which is based on Zeroth law.First Law of Thermodynamics
The first law of thermodynamics defines that energy can neither be created nor destroyed, it can be only transformed from one form to another form. Mathematically, ΔQ = ΔU + ΔW Here, ΔQ is the heat supplied to the system, ΔU is the change in internal energy of the system, and ΔW is work done by the system. Also, ΔW = PΔV, where P is pressure and ΔV is the change in the volume of the system. Thus, ΔQ = ΔU + P ΔVAlso Check - Unit, Dimension & Vector Formula
Sign Conventions in Thermodynamics Work done on the system = Negative Work done by the system = Positive Heat supplied or added to the system = Positive Heat rejected or removed by the system = NegativeDownload PDF Thermodynamic Formula
Work done in different Thermodynamic processes Work done in isobaric (constant pressure) process, W = PΔV Work done in isochoric (constant volume) process, W = PΔV = P * 0 = 0 Work done in isothermal( constant temperature) process, W = -nRTln ( V 2/ V 1) = -2.303nRTlog( V 2/ V 1) Here, n = number of moles of gas R = Gas constant T = temperature of system Work done in adiabatic process,
Also Check - Transmission of Heat Formula
 Also, slope of adiabatic process =
( slope of the isothermal process)
Also, slope of adiabatic process =
( slope of the isothermal process)
Entropy
Entropy is defined as a measure of randomness or disorder of a system. Change in entropy of the system, ΔS = Q rev* T Where Q rev is the heat supplied reversibly and isothermally.Second Law of Thermodynamics
The second law of thermodynamics can be stated as follows Kelvin-Planck Statement: It is not possible to construct a machine which is working in a cycle has the sole effect of extracting heat from a single reservoir and performing a same amount of work. Clausius Statement: I t is impossible to design a machine that works on a cycle and produces no effect other than heat transfer from a cold body to a hot body. Carnot Cycle Carnot cycle is a theoretical cycle that is an ideal reversible closed thermodynamic cycle. It consists of the following four processes: Isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression. The theoretical engine based on this cycle is called as Carnot Engine and according to Carnot theorem, Any system working between a hot reservoir and a cold reservoir can never have higher efficiency than the Carnot engine operating between the same reservoirs. The efficiency of the Carnot Cycle is given by, = 1 -( T 2/ T 1) ( T 1 > T 2 ) Where T 1 is the hot reservoir (source) temperature and T 2 is the the sink temperature.Heat Engine
A heat engine is a device that uses a heated source as a reservoir and transfers heat from there to perform work. There is a rejection of some heat to the sink (cold body). The basic diagram of a heat engine is shown as,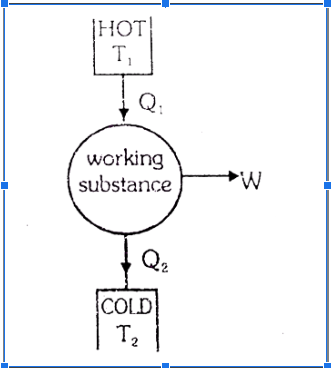 Here Q
1
is the heat extracted from the
hot reservoir and Q
2
is the heat
rejected to the the sink.
W is the work done by the heat engine.
Here Q
1
is the heat extracted from the
hot reservoir and Q
2
is the heat
rejected to the the sink.
W is the work done by the heat engine.

Refrigerator
It is basically a heat engine operated in the reverse direction. The basic diagram is shown as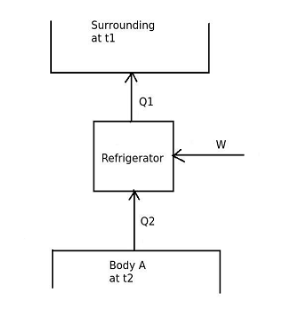 Work done on the system = W
Heat taken from sink = Q
2
Heat rejected to reservoir = Q
1
Now, Q
1
= Q
2
+ W
Work done on the system = W
Heat taken from sink = Q
2
Heat rejected to reservoir = Q
1
Now, Q
1
= Q
2
+ W

Specific Heats
There are two specific heats, one is specific heat at constant volume (C v ) and specific heat at constant pressure (C p ) Specific heat is that the quantity of heat essential to increase the temperature of 1 gram of any substance by 1 degree Centigrade. Specific heat, C = Q* m* T ’ Here, Q is heat gained or lost by the system. T is the change in the temperature of the system. Also C p is related to C v by the relation, C p - C v = R, where R is the universal gas constant.Thermodynamics Formula FAQs
What is internal energy?
Internal energy is the sum of all the energies possessed by the atoms or molecules of a substance.
The first law of thermodynamics is based on?
The first law of thermodynamics is based on the law of conservation of energy.
How are two specific heats related to each other?
The two specific heats are related as,
Cp/Cv =γ and Cp - Cv = R
What is the net work done in the isochoric process?
The net work done in the isochoric process is zero and there is no change in the volume of the system.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App











