Heat Radiation
Heat And Thermodynamics of Class 11
The process in which heat is transferred from one place to the other without any intervening medium is called radiation. All bodies at all temperatures and at all times radiate energy in the form of electromagnetic waves, called radiant energy. Emission rate is faster at higher temperatures. In this radiant energy, electromagnetic waves of wavelength ranging from 10-4 mm to 1 mm are called infrared radiation or heat radiation. According to prevost’s theory of exchange besides radiating heat radiation or thermal radiation all bodies also absorb part of the thermal radiation falling on them emitted by the surrounding bodies. If a body radiates more, what it absorbs, its temperature falls and vice versa.
Basic Definitions
(i) Perfectly Black Body
A body which absorbs all the radiations incident on it is called a perfectly black body.
(ii) Absorptive Power of a surface (a)
The ratio of the radiant energy absorbed by it in a given time to the total radiant energy incident on it in the same time is called the absorptive power (a) of the surface. Since it is a pure ratio it has no units and dimensions. The absorptive power of a perfectly black body is maximum and its value is unity.
a ≤ 1
(iii) Spectral Absorptive Power (aλ)
Absorptive power refers to all wavelengths (total radiant energy). However, any surface will have different values of absorptive powers for different wavelengths. A surface may be a good absorber for a wavelength λ1 and bad absorber for wavelength λ2, it means its absorptive power for wavelength λ1 is greater than the absorptive power for λ2.
Thus, spectral absorptive power aλ is defined as the ratio of the radiant energy of a given wavelength absorbed by a given surface in a given time to the total radiant energy of that wavelength incident in the same time on the same surface. Or we can say that it is absorptive power for that particular wavelength. It is now obvious that
a =
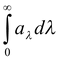 (5.43)
(5.43)
aλ ≤ 1
For perfectly black bodyaλ = 1
Example: 5.27
100 units of energy is incident on a surface. In this 20 units are of wavelength λ
1
, 30 units are of wavelength λ
2
and rest 50 units are other wavelengths. The total 60 units of energy is absorbed by the surface. In this 60 units 5 units are of λ
1
and 25 units are of λ
2
. Find a,
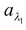 and
and
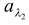 .
.
Solution
Total absorptive power a = 60/100 = 0.6
and spectral absorptive power for λ1 =
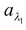 = 5/20 = 0.25
= 5/20 = 0.25
Spectral absorptive power for λ
2
=
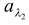 = 25/30 = 0.83
= 25/30 = 0.83
From this example it is clear that total absorption power of the surface is only 0.6 whereas
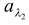 is 0.83 (> 0.6) i.e. the surface is good absorber of wavelength λ2.
is 0.83 (> 0.6) i.e. the surface is good absorber of wavelength λ2.
(iv) Emissive Power (E)
Radiant energy (total energy radiated in the form of electromagnetic radiation) emitted per second per unit area of the surface is called Radiant intensity of the surface. Radiant intensity of a surface depends on its nature and temperature. It has units W/m2. It is maximum for a perfectly black body.
(v) Emissivity (e)
Emissivity or relative emitance (e) has values between 0 and 1, depending on the nature of surface. It has no units and dimensions.
e = 1 for a perfectly black body.
Emissivity gives an idea about relative emittance with respect to a perfectly blackbody. e.g. if emissivity of a surface is 0.6, it means it will radiate 60% of the energy radiated by a perfectly black body under similar conditions.
(vi) Spectral Emissive Power (eλ)
This is emissive power of the surface for a particular wavelength λ.
Obviously,
e =
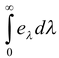 (5.44)
(5.44)
eλ is maximum for a perfectly black body.
(vii) Kirchhoff’s Law
The ratio of emissive power to absorptive power is same for all surfaces at the same temperature and is equal to the emissive power of a perfectly black body at that temperature. That is,

or e/a = constant (5.45)
Similarly,
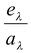 = constant (5.46)
= constant (5.46)
This implies that a good absorber is a good emitter also. In otherwords, a good absorber of a particular wavelength λ is a good emitter of that particular wavelength λ.
(viii) Stefan’s law
According to it the radiant energy emitted by a perfectly black body per unit area per second. (i.e. emissive power) is directly proportional to fourth power of its absolute temperature T, i.e.
E = σT4(5.47)
For any other surface
E = eσT4 (5.48)
where e is the emissivity of the surface, and
σ is the Stefan’s constant
σ = 5.67 × 10-8 Wm-2K-4.
If A is the surface area, then the rate of heat emitted by the body is
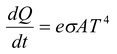 (5.49)
(5.49)
Application of Stefan’s Laws
(i) Cooling by radiation
If a body having temperature T is kept in an environment of temperature To (< T) , the body will lose energy at a rate
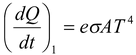
and absorb energy at a rate
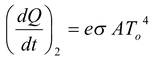
Thus, the net rate of loss of energy
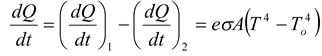 (5.50)
(5.50)
If m be the mass of body and c its specific heat, the rate of loss of heat at temperature T must be
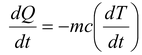 (5.51)
(5.51)
Equating (5.50)and (5.51)
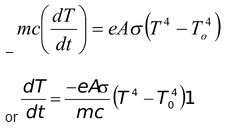 (5.52)
(5.52)
Thus, the rate of cooling (dT/dt) depends on A, m, c, T, To and e ( i.e. nature of radiating surface). Hence greater the emissivity faster will be the cooling.
(ii) Newton’s law of cooling
When the temperature difference between the body and its surrounding is not very large, i.e.T − To = ΔT
therefore, T4 – To4 = [(To + ΔT)4 – To
4
] = To
4
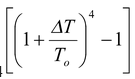
=
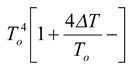 using binomial theorem
using binomial theorem
orT4 – To4 = 4To3 ΔT
Therefore equation (5.52) can be written as
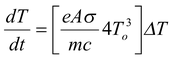 (5.53)
(5.53)
Since the term given in the bracket is constant, therefore, the rate of cooling is proportional to temperature difference between the body and its surroundings provided the temperature difference is not very large from the surrounding. This is called Newton’s Law of Cooling.
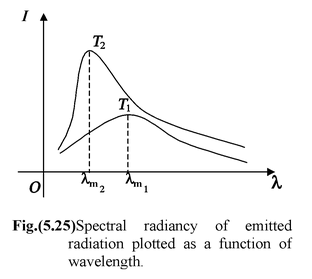
Distribution of Energy in the Spectrum of Black Body
At a given temperature energy (or intensity) is not uniformly distributed among different wavelengths. It first increases with wavelength, reaches a maximum at a particular wavelength (λm) and then decreases with increase in wavelength.
(iii) Wein’s Displacement Law
Products of wavelengths λm corresponding to maximum spectral radiancy and temperature T of the body in kelvin is constant.
i.e.λ m T = b = constant (5.54)
or λ m ∝ 1/T
where b is Wein’s constant having value of 2.89 × 10-3m-K
|
Graphically it can be shown as
T2 > T1
As the temperature of the body increases, the wavelength at which the radiant intensity is maximum shifts toward left. It is called Wein’s displacement law. In solar radiations λm = 4753 Å Hence temperature of sun,
T =
|
|
The area under the curve represents the radiant intensity of radiation at a particular temperature. Since total radiant energy is proportional to fourth power of T, area should also be proportional to fourth power of absolute temperature T.
∴ Area ∝ T 4
Example: 5.28
A sphere, a cube and a thin circular plate all made of the same material and having the same mass are initially heated to 200oC. Which of these objects will cool faster and which one slowest when left in air at room temperature?
Solution
When body cools by radiation, according to Stefan’s law,
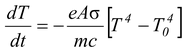
Here m, c, e, T and To are same for all bodies.
so dT/dt ∝ A where A is the surface area
Since for a given mass area of plate is maximum while of sphere is minimum the disc will cool fastest while sphere slowest.
Example: 5.29
A body which has a surface area 5 cm2 and a temperature of 727 oC radiates 300 J of energy each minute. What is its emissivity?
(Stefan-Boltzmann constant σ = 5.67 × 10-8 W/m 2 K4)
Solution
According to Stefan-Boltzmann law, energy radiated per second by a body
P = eσAT4
Here P = (300/60) J/s = 5 J/s, T = 273 + 727 = 1000 K
so e =
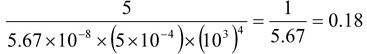
Example: 5.30
A solid copper sphere (density ρ and specific heat c) of radius r at an initial temperature
200 K is suspended inside a chamber whose walls are at almost 0 K. What is the time required for the temperature of the sphere to drop to 100 K?
Solution
According to Stefan’s law the rate of loss of energy due to radiation
P = eAσT4 (i)
Now if the rate of change of temperature of a body of mass m and specific heat c is (dΤ/dt) the rate of loss of heat will be
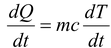 (ii)
(ii)
As equation (i) and (ii) represents the same quantity of energy
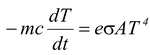
Note that the negative sign shows that temperature decreases with time.
Herem = (4/3) πr3ρ and A = 4πr 2
∴
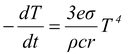
or
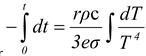
or t =
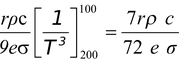 × 10-6 s
× 10-6 s
Example: 5.31
A body cools in 7 minutes from 60 o C to 40 o C. What will be its temperature after the next 7 minutes? The temperature of surroundings is 10 o C.
Solution
According to Newton’s law of cooling,
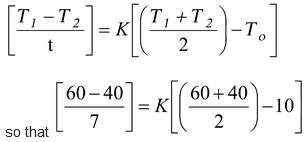
⇒ K = 1/14 (i)
Now if after cooling from 40 oC for 7 minutes the temperature of the body becomes T, according to Newton’s law of cooling
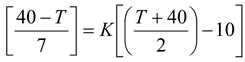
which in the light of equation (i), i.e., K = 1/14 gives
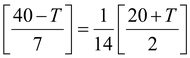
i.e.160 – 4Τ = 20 + Τ orT = 28 o C
Alternative
Solution
According to Newton’s law of cooling,
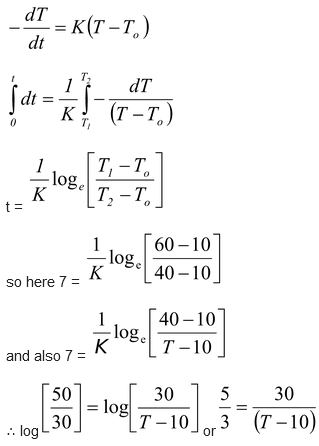
5Τ - 50 = 90 o rΤ = 28 o C

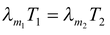
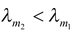
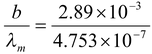 = 6080 K
= 6080 K