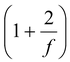Internal Energy of An Ideal Gas
Heat And Thermodynamics of Class 11
Internal Energy of an Ideal Gas
By internal energy of a system we mean energy of ‘disordered’ motion of molecules. Since intermolecular forces are zero in case of an ideal gas, potential energy for an ideal gas is zero. Therefore its total kinetic energy is its internal energy U. Kinetic energy may have three forms – translational (due to translatory motion of molecules), rotational and vibrational. For an ideal gas, the internal energy U of an ideal gas depends upon temperature T only and is directly proportional to it,
i.e.U ∝ T
Specific Heat and Heat Capacity
If a quantity of heat Q produces a change in temperature ΔT in a body, its heat capacity is defined as
Heat capacity C = Q/ΔT (5.13)
The SI unit of heat capacity is JK-1.
The quantity of heat Q required to produce a change in temperature ΔT is also proportional to the mass m of the sample.
Thus, Q = mc ΔΤ (5.14)
where c is called the specific heat of the substance.
Specific heat may be defined as the heat capacity per unit mass.
c = Heat capacity/mass (5.15)
It is sometimes convenient, especially in the case with gases, to deal with the number of moles n of a substance rather than its mass. Then,
Q = n Cm ΔT(5.16)
where Cm is the molar specific heat, measured in J/mol-K (or cal/mol-K)
Since n = m/M where M is the molar mass, then
Cm = Mc
The specific heat of a substance usually varies with temperature.
The specific heat changes abruptly when the substance transforms from solid to liquid, or from liquid to gas. It also depends on the conditions under which the heat is supplied. For example, the specific heat of a gas kept at constant pressure Cp is different from its specific heat at constant volume Cv. For air, Cv = 0.17 cal/g-K and Cp = 0.24 cal/g-K For solids and liquids the difference is generally small, and in practice Cp is usually measured.
CP, CV and γ of an ideal gas
Here we will learn the kinetic interpretation of the following formulae.
(i)Molar specific heat at constant volume
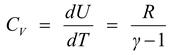
(ii)Molar specific heat at constant pressure CP = CV + R
(iii)Adiabatic exponent
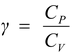
*Molar specific heat = Heat required to raise the temperature of 1 mole of a gas by 1 °C.
*In
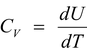 , U is the internal energy of 1 mole of the gas.
, U is the internal energy of 1 mole of the gas.
Degree of Freedom f
Degree of freedom (f) is defined as the number of possible independent ways in which a system can have energy. The independent motions can be translational, rotational or vibrational or any combination of them. A particle moving in a straight line can have only one degree of freedom. i.e., translational degree of freedom. Similarly a particle moving in a plane have two translational degrees of freedom and a particle free to move in space have three translational degrees of freedom.
Monatomic gas molecules can be considered as point masses moving in space and they will have only three translational degrees of freedom. However, this does not hold good with polyatomic gases. In a polyatomic molecule we have to take rotational motion of atoms about their centre of mass and the vibrational motion of the atoms relative to each other. Thus, we must write the molecular kinetic energy as
E = translational energy + rotational energy + vibrational energy
As the temperature of a gas increases, the different components of the molecular energy also increase. But each component increases in a different manner. Vibrational energy depends on the strength of the bonding of the atoms in the molecule. The stronger the ionic bonds, the more difficult it is to increase the vibrational energy. On the other hand, the rotational energy depends on the geometry (moment of inertia) of the molecule. But since vibrational energy come into picture only at high temperatures, vibrational degrees of freedom are not taken into account unless stated in the question.
(i)A monatomic gas has 3 degrees of freedom (all translational). Although a monatomic molecules can also rotate but due to its small moment of inertia rotational kinetic energy is insignificant.
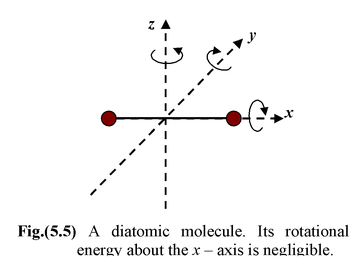
(ii)A diatomic gas such as H
2
, O
2
etc. are made up of two atoms joined rigidly to one another through a bond. This cannot only move bodily, but also rotate about any one of the three
co-ordinate axes. However, its moment of inertia about the axis joining two atoms is negligible.
|
Hence it can have only two rotational motions. Thus, a diatomic molecule has five degrees of freedom, three translational and two rotational. (iii)A nonlinear polyatomic gas molecule such as H 2 O, NH 3 etc. can rotate about any of three co-ordinate axes. Hence it has six degrees of freedom, three translational and three rotational. However, a linear polyatomic gas molecule like CO 2 has five degrees of freedom three translational and two rotational (like a diatomic molecule). |
|
Law of Equipartition of Energy
According to this law the energy of an ideal gas is equally distributed in each degree of freedom. The average kinetic energy per degree of freedom per molecule is 1/2 kT. The kinetic energy per degree of freedom per mole is 1/2RT . In general, the kinetic energy per molecule is 1/2fkT and that per mole is 1/2fRT.
Note that translational degrees of freedom for all the three types of gases are 3. Therefore, translational kinetic energy of an ideal gas molecule (whether it is monatomic, diatomic or polyatomic) is 3/2kT. This is in agreement with the result of kinetic theory of gases.
Because according to it –
Translational KE of one molecule of an ideal gas =
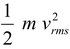
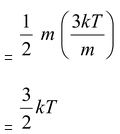
Similarly total internal energy (U) of one mole of a diatomic gas = 5/2 RT
In this 3/2RT is translational KE and 2/2 RT or simply RT is rotational KE.
Expressions of U, CP, CV and γ for a monatomic, diatomic and polyatomic gas
For one mole of an ideal gas
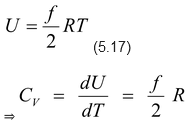
CP = CV + R =
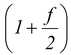 R(5.19)
R(5.19)
γ =
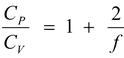 (5.20)
(5.20)
|
Type of Gas |
Degrees of Freedom f |
Internal Energy U |
CV =
|
CP =
|
γ =
|
|
Monatomic |
3 |
3/2 RT |
3/2 R |
5/2 R |
1.67 |
|
Diatomic |
5 |
5/2 RT |
5/2 R |
7/2 R |
1.4 |
|
Polyatomic |
6 |
3 RT |
3 R |
4 R |
1.33 |
Mixture of Gases
Following results are helpful for a mixture of gases.
Umix = U 1 + U 2 + …. (5.21)
Mmix =
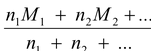 (5.22)
(5.22)
Pmix = P 1 + P2 + …. (5.23)
(CV)
mix
=
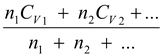 (5.24)
(5.24)
(CP)
mix
=
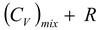 (5.25)
(5.25)
γ
mix
=
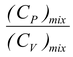 (5.26)
(5.26)
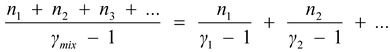 (5.27)
(5.27)
Example: 5.10
A vessel contains a mixture of 7 g of nitrogen and 11 g of carbon dioxide at temperature
T = 290 K. If pressure of the mixture P = 1 atm, calculate its density (R = 8.31 J/mol K).
Solution
As molecular weights of N2 and CO 2 are 28 and 44, and n = (m/M),
nN = 7/28 = 1/4 and nC = 11/44 = 1/4
son = nN + nC = 1/4 + 1/4 = 1/2
Now as according to gas equation PV = nRT,
V =
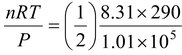 = 1.19 × 10
-2
m
3
= 1.19 × 10
-2
m
3
Mass of the gas is given by
m = 7 + 11 = 18 g = 18 × 10 -3 kg
∴ρ = (m/V) = (18 × 10 -3 )/(1.19 × 10 -2 ) = 1.5 kg/m 3
Example: 5.11
Two perfect gases at absolute temperatures T1 and T2 are mixed. There is no loss of energy. Find the temperature of the mixture if the masses of the molecules are m1 and m2 and the number of molecules in the gases are n 1 and n 2 .
Solution
According to the kinetic theory of gases, the kinetic energy of an ideal gas molecule at temperature T is given by KE = (3/2)kT. And as there is no force of attraction among the molecules of a perfect gas, PE of the molecule is zero. So the energy of a molecule of perfect gas,
E = KE + PE =
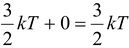
Now if T is the temperature of the mixture, by conservation of energy, i.e.
n 1 E 1 + n 2 E 2 = (n 1 + n 2 )E
we have n
1
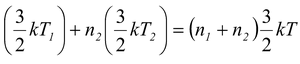
i.e.T =
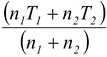
Example: 5.12
One mole of a monatomic gas is mixed with 3 moles of a diatomic gas. What is the molar specific heat of the mixture at constant volume? (R = 8.31 J/mol K)
Solution
For monatomic gas Cv = 3/2R while of diatomic, 5/2R , so by conservation of energy ,
Cv =
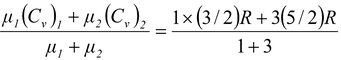
i.e.Cv =
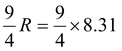 = 18.7 J/mol K
= 18.7 J/mol K

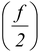 R
R
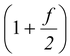 R
R