Thermodynamics
Heat And Thermodynamics of Class 11
Thermodynamics is concerned with the work done by a system and the heat it exchanges with its surroundings. We are concerned only with work done by a system on its surroundings or on the system by the surroundings. We are not concerned with internal work done by one part of a system on another.
Heat vs. Work
Heat is the energy transferred between two bodies as a consequence of a temperature difference between them. In contrast, work is a mode of energy transfer in which the point of application of a force moves through a displacement and is not associated with a temperature difference.
Both heat and work are “energy in transit” from one body to another during the operation of some process, once the process stops, heat and work have no meaning.
Mechanical Equivalent of Heat
It has been concluded from Joule’s experiment that the mechanical work required to produce a given change in temperature is in fixed proportion to the heat required for the same change in temperature. This constant factor is called the mechanical equivalent of heat.
1 calorie = 4.186 J (5.28)
Thus, a change in the state of a system produced by the addition of 1 calorie of heat may also be produced by the performance of 4.186 J of work on the system.
Thermodynamic Work
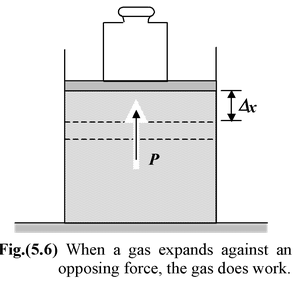
Figure(5.6) shows a gas confined to a cylinder by a weight on a movable piston. Our system is the gas, whereas the cylinder and the piston form the environment. If the piston is allowed to move upward, the gas expands and does work on it. To calculate the work done by the gas, we assume that the process is quasistatic. In a quasistatic process the thermodynamics variables (P, V, T, n, etc.) of the system and its surroundings change infinitely slowly. Thus, the system is always arbitrarily close to an equilibrium state, in which it has a well-defined volume, and the whole system is characterized by single value of the macroscopic variables. To ensure that the piston moves very slowly, there must be some force, for example, provided by a weight, directed opposite to that due to the pressure. If the piston were to move suddenly, the rapid expansion would involve turbulence and the pressure would not be uniquely defined.
|
|
|
When the piston rises by dx, the work dW done by the gas is dW = F dx = (PA) dx where A is the cross-sectional area of the piston. Since the change in volume of the gas is dV = A dx, the work may be expressed as
(Quasistatic) dW = P dV (5.29 a)
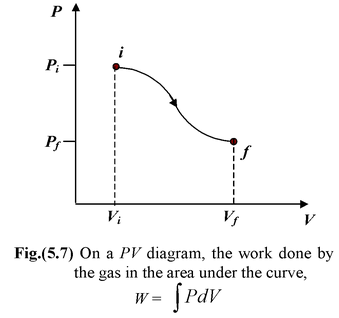
As a quasistatic process evolves, P and V are always uniquely defined. This allows us to depict the process on a PV diagram such as figure(5.7). When the system is taken quasistatically from the equilibrium state i to another equilibrium state f, the total work done by the system is
W =
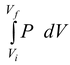 (5.29 b)
(5.29 b)
In figure the work is represented by the area under the curve. If Vf> Vi, the work done by the gas is positive. If the volume decreases, the work done by the gas is negative. This may be interpreted as positive work done on the gas by the environment. The work done depends not only on the initial and final states but also on the details of the process, that is, the thermodynamic path between the states. Therefore, we need to know how the pressure varies with the volume.