Friction
Laws Of Motion of Class 11
Whenever the surface of a body slides over that of another, each body exerts a force of friction on the other, parallel to the surfaces. The force of friction on each body is in a direction opposite to its motion relative to the other body.
The force of friction comes into action only when there is a relative motion between the two contact surfaces or when an attempt is made to have it.
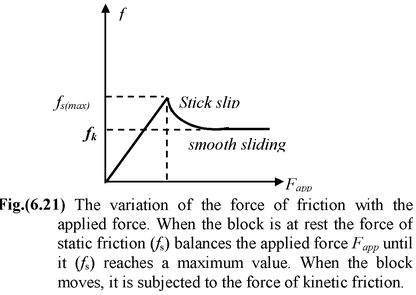
It is a self adjusting force, it can adjust its magnitude to any value between zero and the limiting (maximum) value i.e
0 ≤ f ≤ f max
The frictional force acting between any two surfaces at rest with respect to each other is called the force of static friction. And the frictional force acting between surfaces in relative motion with respect to each other is called the force of kinetic friction or sliding friction.
LAWS OF FRICTION
The limiting (or maximum) force of friction is proportional to the normal force that keeps the two surfaces in contact with each other, and is independent of the area of contact between the two surfaces. Mathematically,
fmax = µN(6.5)
PROPERTIES OF FRICTION1.If the body does not move, then the static frictional force fs and the external force F parallel to the surface are equal in magnitude and fs is directed opposite to F. If the external force F increases fs increases. 2.The maximum value of static friction is given by fs(max) = µsN (6.6) where µs = static coefficient of friction and N is the magnitude of the normal reaction. If the external force F exceeds fs(max) then the body slides on the surface. |
|
3.If the body begins to slide along the surface, the magnitude of the frictional force rapidly decreases to a constant value of fk given by
fk = µkN (6.7)
where µk is the coefficient of kinetic friction.
|
(a) |
(b) |
(c) |
|
(d) |
(e) |
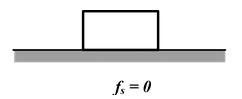
Fig.(6.22) (a)The friction force on a stationary block is zero.
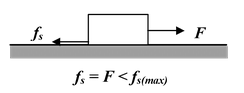
(b)As long as the external force is less than the maximum friction force, fs = F.
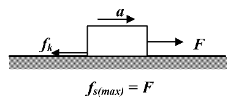
(c)At the limiting case fs(max) = F, the block is about to slide.
(d) As the value of F slightly increases beyond fs(max) , the block “breaks away” accelerating suddenly to the right.
(e) If the block is to move with a constant velocity, the applied force must be reduced, because μk < μs.
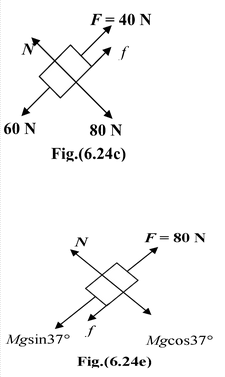
Example: 6.12
|
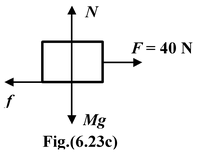
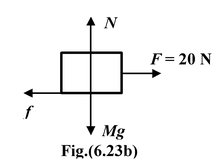
A block of mass M = 10 kg is placed at rest on a horizontal surface as shown in the figure. The coefficient of friction between the block and the surface is µs = 0.3 and μk = 0.2. It is pulled with a horizontal force F. Find the magnitude of the friction if (a) F = 20 N(b) F = 40 N |
|
Solution
|
The maximum value of friction force is fs(max) =µsN = µsMg orfs(max) = (0.3) (10) (10) = 30 N
(a)To keep the block stationary the magnitude of friction force should be
(b)fs(max) < F so the body moves and now force of friction f = μkN = 0.2(10)(g) = 20 N |
|
|
Note that in this case friction force is unable to keep the block stationary and the block accelerates with
a =
|
|
Note that friction force is not always equal to µsN. It is the limiting or maximum value of static friction. At any stage friction may attain any value between 0 and µsN.
0 ≤ f ≤ µsN(6.8)
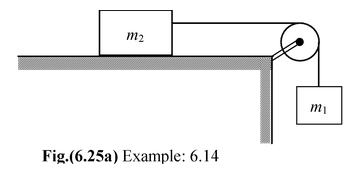
Example: 6.13
|
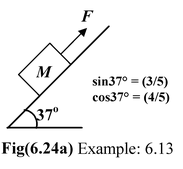
A block of mass, M = 10 kg, is placed at rest on an inclined plane and is being pulled upward with a force F parallel to the incline as shown in the figure. The coefficient of friction between the block and the incline is µS = 0.3. Find the magnitude and direction of the friction force acting on the block if (a) F = 40 N(b) F = 80 N |
|
Solution
|
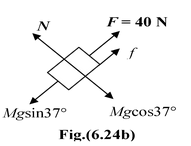
(a)Since Mg sin 37° > F therefore, the block has a tendency to slide downward in the absence of friction. Thus, the frictional force will act upward on the block to oppose the relative motion between the two. Now, to keep the block stationary, the force of friction should be f = Mg sin37° − F orf = 60 − 40 = 20 N |
|
|
|
The maximum value of friction is fmax = µsN = µsMg cos 37° orfmax = (0.3) (10) (10) (4/5) = 24 N Since f < fmax, therefore, the frictional force acting on the block is f = 20 N (upward)
|
|
|
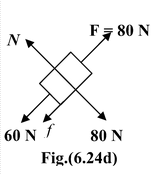
(b)Since Mgsin37° < F, therefore the block has a tendency to slide upward in the absence of friction The frictional force acts downward on block.
Now, to keep the block stationary the force of friction should be
f = F − Mg sin 37°
orf = 80 − 60 = 20 N
Since f < fmax therefore the force of friction acting on the block is f = 20 N (downward)
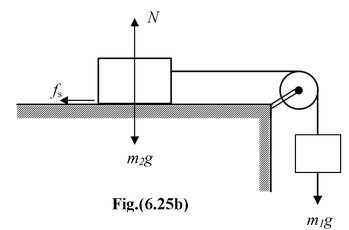
Example: 6.14
|
For the system shown in the figure, the coefficient of static and kinetic friction between the block m2 and the horizontal surface is µs and µk. If m 2 = 10 kg, µs= 0.4 and µk = 0.35 (a)find the maximum value of m1 so that the block m2 does not move. (b)And also, if m1 = 5 kg, find the acceleration of the system. |
|
Solution
|
(a)The force which accelerates the system is m1g, while the opposing force is fs. For maximum value of m1 under equilibrium condition. (m1g)max = fs(max) =µsm 2 g orm 1 (max) = µsm 2 hereµs = 0.4, m 2 = 10 kg Thus, m 1 (max) = (0.4) (10) = 4 kg |
|
(b)When m 1 = 5 kg, the system starts accelerating; m1 accelerates downward and m2 accelerates rightward. Let a be the acceleration of the system. m 2 is moving so fk will act
m 1 g – T = m 1 a
T - μkm
2
g = m
2
a ora =
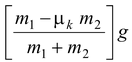
Putting m 1 = 5kg; m 2 = 10 kg; µk = 0.35; g = 10 m/s 2
We get, a = [5 - (0.35)(10)/5 + 10] x (10)= 1 m/s 2

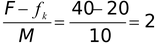 m/s
2
m/s
2