Unit Cell

Solid State of Class 12

A unit cell is the smallest repeating unit in space lattice which when repeated over and over again results in a crystal of the given substance. Unit cell may be also defined as a three dimensional group of lattice points that generates the whole lattice on repetition.

BRAVAIS LATTICES

The French crystallographer August Bravais in 1848 showed from geometrical consideration that there can be only 14 different ways in which similar points can be arranged in a three dimensional space. Thus the total no. of space lattices belonging to all the seven basic crystal system but together is only 14.

Types of unit cells

1. Simple unit cell having lattice points only at the corners is called simple, primitive or basic unit cell. A crystal lattice having primitive unit cell is called simple crystal lattice

2. Face centred cubic lattice (fcc) - A unit cell in which the lattice point is at the centre of each face as well as at the corner.

3. Body centred cubic lattice (bcc) - A unit cell having a lattice point at the centre of the body as well as at the corners.

Another type of unit cell, called end centred unit cell is possible for orthorhombic and monoclinic crystal types.

In an end centred there are lattice points in the face centres of only one set of faces in addition to the lattice pints at the corners of the unit cell

The various types of unit cells possible for different crystal classes (in all seven) are given below in tabular form

Crystals class	Axial distances	Angles	Possible types of unit cells	Examples
Cubic	a = b = c	α = β = γ = 90°	Primitive, Body centred face centred	Copper , KCl, NaCl zinc blende, diamond
Tetragonal	a = b ≠ c	α = β = γ = 90°	Primitive, body centred	SnO₂, White tin, TiO₂
Orthorhombic	a ≠ b ≠ c	α = β = γ = 90°	Primitive body centred, face centred end centred	Rhombic sulphur, KNO₃, CaCO₃
Hexagonal	a = b ≠ c	α = β = 90° γ = 120°	Primitive	Graphite, Mg, ZnO
Trigonal or Rhombohedral	a = b = c	α = β = γ ≠ 90°	Primitive	(CaCO₃) Calcite, HgS(Cinnabar)
Monoclinic	a ≠ b ≠ c	α = β = 90° γ ≠ 90°	Primitive and end centred	Monoclinic sulphur, Na₂SO₄.10H₂O
Triclinic	a ≠ b ≠ c	α ≠ β ≠ γ ≠ 90°	Primitive	K₂Cr₂O₇, CuSO₄.5H₂O

The Bravais space lattices associated with various crystal system are show in fig below

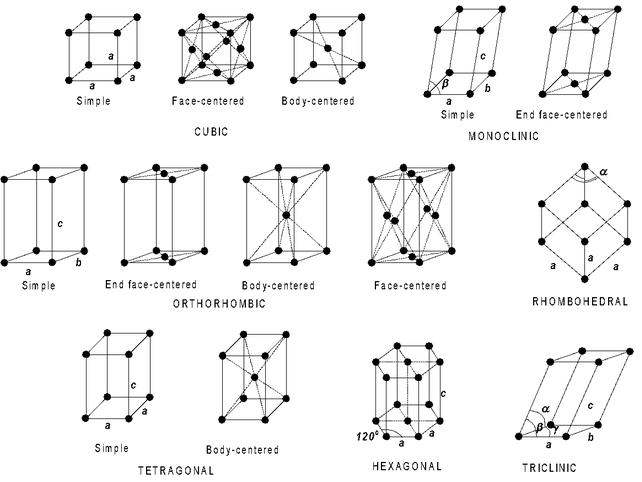
Unit Cell

CALCULATION OF NUMBER OF PARTICLES PER UNIT CELL

The no of atom in a unit cell can be calculated by keeping in view following points

1. An atom at the corners is shared by eight unit cells. Hence the contribution of an atom at the corner to a particular cell = 1/8

2. An atom at the face is shared by two unit cells. Hence the contribution of an atom at the face to a particular cell = 1/2

3. An atom at the edge centre is shared by four unit cells in the lattice and hence contributes only 1/4 to a particular unit cell.

4. An atom at the body centre of a unit cell belongs entirely to it, so its contribution = 1

The number of atoms per unit cell is in the same ratio as the stoichiometry of the compound. Hence it helps to predict the formula of the compound

SIMPLE CUBIC LATTICE

There are eight atoms at the corners. Each corner atom makes 1/8 contribution to the unit cell.

∴ No. of atoms present in the unit cell = 1/8 x 8 = 1

BODY CENTRED CUBIC (BCC)

BCC has 8 atoms at the corners and one atom, within the body. Each corner atom makes 1/8 contribution and the contribution of atom within the body = 1

∴ No of atoms present in bcc = 1/8 x 8(at corner) + 1(at the body centre)

= 1+1 =2