Close Packing In Crystals

Close Packing In Crystals

In order to understand the packing of the constituent particles in a crystal, it is assumed that these particles are hard spheres of identical size (eg those of metal). The packing of these spheres takes place in such a way that they occupy the maximum available space and hence the crystal has maximum density. This type of packing is called close packing.

TWO DIMENSIONAL PACKING

When the rows are combined touching each other, the crystal plane is obtained. The rows can be combined in two different ways

(i) The particles when placed in the adjacent rows, show a horizontal as well as vertical alignment and form squares. This type of packing is called square close packing

(ii) The particles in every next row are placed in the depressions between the particles of the first row. The particles in the third row will be vertically aligned with those in the first row. This type of packing gives a hexagonal pattern and is called hexagonal close packing

Square close packing (coordination no 4) Hexagonal close packing(coordination no 6)

THREE DIMENSIONAL PACKING

In two dimensional packing, a more efficient packing is given by hexagonal close packing. In order to develop three dimensional close packing let us retain the hexagonal close packing in the first layer. If the spheres in the second layer are just placed over the spheres in the first layer so that the spheres in the two layers are vertically aligned, its voids will come above the voids in the first layer. This is an inefficient way of filling the space.

When the second layer is placed in such a way that its spheres find place in the ‘b’ voids of the first layer, the ‘c’ voids will be left unoccupied. Since under this arrangement no sphere can be placed in them, (c voids), i.e. only half the triangular voids in the first layer are occupied by spheres in the second layer (i.e. either b or c)

There are two alternative ways in which spheres in the third layer can be arranged over the second layer

(1) When a third layer is placed over the second layer in such a way that the spheres cover the tetrahedral or ‘a’ voids; a three dimensional closest packing is obtained where the spheres in every third or alternate layers are vertically aligned (i.e. the third layer is directly above the first, the fourth above the second layer and so on) calling the first layer A and second layer as layer B, the arrangement is called ABAB …………. pattern or hexagonal close packing (hcp) as it has hexagonal symmetry.

(2) When a third layer is placed over the second layer in such a way that spheres cover the octahedral or ‘c’ voids, a layer different from layers A and B is produced. Let it be layer ‘C’. Continuing further a packing is obtained where the spheres in every fourth layer will be vertically aligned to the spheres present in the first layer. This pattern of stacking spheres is called ABCABC ……….. pattern or cubic close packing (ccp). It is similar to face centred cubic (fcc) packing as it has cubic symmetry

In both hcp and ccp methods of stacking, a sphere is in contact with 6 other spheres in its own layer. It directly touches 3 spheres in the layer above and three spheres in the layer below. Thus sphere has 12 close neighbours. The number of nearest neighbours in a packing is called coordination number. In close packing arrangement (hcp & ccp) each sphere has a coordination number of 12.

PACKING FRACTIONS

Both of the above patterns of packing (i.e. hcp & ccp) though different in form are equally efficient. They occupy the maximum possible space which is about 74% of the available volume. Hence they are called closest packing.

In addition to the above two types of arrangements a third type of arrangement found in metals is body centred cubic (bcc) in which space occupied is about 68%.

CALCULATION OF THE SPACE OCCUPIED

In simple cubic unit cell

Volume of the cube = a³= (2r)³ = 8r³

∴ Fraction of the space occupied = 4/3πr³/8r³ = 0.524

∴ % occupied = 52.4 %

But from the right angled triangle ACD

AD=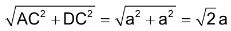

√2a = 4r or a = 4/√2r

∴ volume of cube = (4√2r)³  = 64/2√2r³

percentage of space occupied by sphere

=

In body centred cubic unit cell

Let ‘r’ be the radius of sphere and ‘a’ be the edge length of the cube

As the sphere at the centre touches the sphere at the corner. Therefore body diagonal

AD = 4r

Face diagonal AC =

In right angled triangle ACD =

∴Volume of the unit cell = a³ =

No. of spheres in bcc = 2

∴ volume of 2 spheres = 2×4/3πr³

∴ percentage of space occupied by spheres

=

Other Resourceful Topics

• Structure of Ionic Compounds
• Properties of Solids 
• Super Conductivity