Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
A quadrilateral is a closed shape and a type of polygon that has four sides, four vertices and four angles. It is formed by joining four non-collinear points. The sum of interior angles of quadrilaterals is always equal to 360 degrees.
What is the important formula of understanding quadrilaterals Class 8?
= p×p, p is side. = 1/2(d1×d2), d1 and d2 are diagonals. d1×d2, d1, and d2 are diagonals.
Why is it called quadrilateral?
A quadrilateral is a polygon having four sides, four angles, and four vertices. The word 'quadrilateral' is derived from the Latin words 'quadri,' which means four, and 'latus', which means side.
What type of quadrilateral has all sides equal?
Four sides of equal length - Rhombus and Square are the quadrilaterals with four sides of equal length.
CBSE Class 8 Maths Notes Chapter 3 Understanding Quadrilaterals
Here we have provided CBSE Class 8 Maths Notes Chapter 3 Understanding Quadrilaterals for the ease of students so that they can prepare better for their exams.
Neha Tanna23 Aug, 2024
Share
CBSE Class 8 Maths Notes Chapter 3:
Chapter 3 of CBSE Class 8 Maths, "Understanding Quadrilaterals," focuses on the properties and classifications of quadrilaterals. It begins by defining polygons and moves on to various types of quadrilaterals, such as parallelograms, rectangles, rhombuses, and squares.
The chapter covers the properties of angles, sides, and diagonals of these shapes, including important theorems. Special emphasis is placed on convex and concave polygons and the sum of interior angles. By the end, students understand how to identify different quadrilaterals based on their properties and solve problems related to their angles and sides.
CBSE Class 8 Maths Notes Chapter 3 Overview
Chapter 3 of CBSE Class 8 Maths, titled "Understanding Quadrilaterals," delves into the study of four-sided polygons and their properties. The chapter begins with an introduction to polygons, including their classification based on the number of sides. It further explores convex and concave polygons, emphasizing the difference between them.
The primary focus of the chapter is on quadrilaterals, which are polygons with four sides. Students learn about various types of quadrilaterals such as parallelograms, rectangles, squares, rhombuses, and trapeziums, each with distinct properties related to their sides, angles, and diagonals.
A significant part of the chapter is dedicated to understanding the sum of the interior and exterior angles of polygons, with the key formula being that the sum of the interior angles of a quadrilateral is always 360°.
CBSE Class 8 Maths Notes Chapter 3 PDF Download
In this, students can classify quadrilaterals, understand their geometric properties, and solve related problems using angle sum properties and other key theorems. Hence, here we have provided CBSE Class 8 Maths Notes Chapter 3 Understanding Quadrilaterals pdf -
CBSE Class 8 Maths Notes Chapter 3 Understanding Quadrilaterals
Here we have provided CBSE Class 8 Maths Notes Chapter 3 PDF -
The fundamental ideas of quadrilaterals, various quadrilateral types and their properties, various curves, polygons, and some quadrilateral theorems—such as the angle sum property of quadrilaterals—will all be covered in detail in the class 8 chapter "Understanding Quadrilaterals."
What are Quadrilaterals?
Quadrilaterals are one type of polygon which has four sides and four vertices and four angles along with 2 diagonals. There are various types of quadrilaterals.
Types of Quadrilaterals
The classification of quadrilaterals are dependent on the nature of sides or angles of a quadrilateral and they are as follows:
Trapezium
Kite
Parallelogram
Square
Rectangle
Rhombus
Revisiting Geometry
As is well known, geometry is a discipline of mathematics that examines various shapes, their characteristics, and the construction of lines, angles, and other polygons. Two basic categories for geometry are plane geometry (two dimensions) and solid geometry (three dimensions).
Introduction to Curves
When multiple points are linked without removing the pencil from the paper or retracing any piece, a curve is the geometric form that results. Essentially, it's a line that doesn't have to be straight.
The various types of curves are:
Open curve: An
open curve
is a curve in which there is
no path
from any of its point to the
same point
.
Closed curve: A
closed curve
is a curve that forms
a path
from any of its point to the
same point
.
A curve can be :
A closed curve:
An open curve:
Simple open and closed curves:
Polygons
A polygon is a basic closed curve composed solely of line segments.
Polygons come in many different forms, such as squares, rectangles, pentagons, etc.
A polygon's sides do not intersect with one another.
Classification of Polygons on the Basis of Number of Sides / Vertices
Polygons are categorised based on how many sides they have. The many polygon types are shown below according to how many sides they have:
When there are three sides, it is
triangle
When there are four sides, it is
quadrilateral
When there are fives sides, it is
pentagon
When there are six sides, it is
hexagon
When there are seven sides, it is
heptagon
When there are eight sides, it is
octagon
When there are nine sides, it is
nonagon
When there are ten sides, it is
decagon
Diagonals
A polygon's diagonal is the section of a line that joins two of its non-consecutive vertices.
Polygons on the Basis of Shape
Based on their shape, polygons can be categorised as convex or concave.
A polygon that has at least one interior angle greater than 90 degrees is said to be concave. At least some of the diagonals of concave polygons are located in their exterior.
Any polygon with all of its internal angles smaller than 180 degrees is said to be convex. Convex polygons don't have any diagonal segments on the outside.
Polygons on the Basis of Regularity
On the basis of regularity, polygons can also be divided into regular and irregular types.
A polygon is referred to as regular when it is both equilateral and equiangular. Every side and every angle in a regular polygon is equal. For instance: Square
An irregular polygon is one that is not regular, that is, it is not equilateral or equiangular. Rectangle, for instance
Angle Sum Property of a Polygon
The angle sum property of a polygon states that the total of a polygon's internal angles is equal to (n-2)×180∘, where n is the polygon's side count.
As we can see for the quadrilateral above, two triangles result from joining one of the diagonals.
The total interior angles of the quadrilateral, or 360∘ = (4−2)×180∘, are equal to the sum of all the internal angles of the two triangles.
Therefore, we can create (n – 2) non-overlapping triangles that will perfectly cover any polygon with n sides.
The
sum of the interior angles of the polygon
will be equal to the
sum of the interior angles of the triangles
=
(
n
−
2
)
×
180
∘
Sum of Measures of Exterior Angles of a Polygon
The
sum
of the measures of the
external angles
of any
polygon
is
360
∘
.
Properties of Parallelograms
The following are the important properties of parallelogram:
The opposite sides of a parallelogram are equal and congruent.
Diagonals of a parallelogram bisect each other.
The diagonals of parallelogram bisect each other and produce two congruent triangles
The opposite angles of a parallelogram are congruent.
Elements of a Parallelogram
There are
four sides
and
four angles
in a parallelogram.
The
opposite sides
and
opposite angles
of a parallelogram are
equal
.
In the parallelogram ABCD, the sides
¯
¯¯¯¯¯¯
¯
A
B
and
¯
¯¯¯¯¯¯¯
¯
C
D
are
opposite
sides and the sides
¯
¯¯¯¯¯¯
¯
A
B
and
¯
¯¯¯¯¯¯
¯
B
C
are
adjacent sides
.
Similarly,
∠
A
B
C
and
∠
A
D
C
are
opposite angles
and
∠
A
B
C
and
∠
B
C
D
are
adjacent angles
.
Angles of a Parallelogram
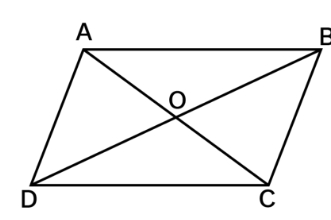The
opposite angles
of a parallelogram are
equal
.
In the parallelogram ABCD,
∠
A
B
C
=
∠
A
D
C
and
∠
D
A
B
=
∠
B
C
D
.
The
adjacent angles
in a parallelogram are
supplementary
.
∴
In the parallelogram ABCD,
∠
A
B
C
+
∠
B
C
D
=
∠
A
D
C
+
∠
D
A
B
=
180
∘
For example,
In the given parallelogram (RING), ∠R = 70°. Now, we have to find the remaining angles.
As we know, the opposite angles of a parallelogram are equal, we can write:
∠R = ∠N = 70°.
And we know, the adjacent angles of a parallelogram are supplementary, we get
∠R + ∠I = 180°
Hence, ∠I = 180° – 70° = 110°
Therefore, ∠I = ∠G = 110° [Since ∠I and ∠G are opposite angles]
Hence the angles of a parallelogram are ∠R = ∠N = 70° and ∠I = ∠G = 110°.
Diagonals of a Parallelogram
At the point of intersection, a parallelogram's diagonals split apart.
Given below is the parallelogram ABCD, where OA = OC and OB = OD.
Consider an example, if OE = 4cm and HL is five more than PE, find the measure of OH.
Given that, OE = 4 cm and hence, OP = 4cm [Since OE = OP]
Hence PE =OE + OP = 4cm + 4cm = 8 cm
Also given that, HL is 5 more than PE,
Hence, HL = 5 + 8 = 13 cm.
Therefore, OH = HL/2 = 13/2 = 6.5 cm
Therefore, the measurement of OH is 6.5 cm
Properties of Special Parallelograms
Rectangle
A rectangle is a parallelogram where all of the angles add up to 90 degrees.
Properties -
A rectangle has equal and parallel opposite sides.
A rectangle's diagonals are all the same length.
A rectangle's internal angles are all equal to ninety degrees.
At the intersection, the diagonals of a rectangle cut each other in half.
Square
A
square
is a
rectangle
with
equal sides
. All the properties of a rectangle are also true for a square.
In a square the diagonals: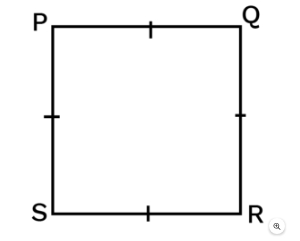
bisect one another
are of equal length
are perpendicular to one another
Rhombus
One of the unique instances of a parallelogram is a rhombus. Every side in a rhombus is equal, as are the sides that face each other.
Benefits of CBSE Class 8 Maths Notes Chapter 3
The benefits of CBSE Class 8 Maths Notes for Chapter 3 Understanding Quadrilaterals are:
Clear Conceptual Understanding
: These notes simplify complex concepts related to quadrilaterals, helping students grasp the properties of various four-sided polygons easily.
Quick Revision
: The notes provide a concise overview of the chapter, allowing students to revise quickly before exams or class tests.
Step-by-Step Explanation
: Each type of quadrilateral, along with its properties (such as angles, sides, and diagonals), is explained systematically, aiding in better comprehension.
Problem-Solving Skills
: By covering the angle sum property and key theorems, these notes enhance students' ability to solve geometry-related problems more efficiently.
Visual Learning
: Diagrams and geometric representations of quadrilaterals help in visualizing the concepts, making it easier to understand and remember.
Exam-Oriented Preparation
: These notes are aligned with the CBSE syllabus, focusing on important topics, ensuring that students are well-prepared for exams.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
The
opposite angles
of a parallelogram are
equal
.
In the parallelogram ABCD,
bisect one another
are of equal length
are perpendicular to one another
