Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Factorisation is the process of breaking down an algebraic expression or a number into simpler components, called factors, that when multiplied together give the original expression or number.
Why is factorisation important in algebra?
Factorisation simplifies algebraic expressions, making it easier to solve equations, simplify problems, and understand mathematical relationships. It is fundamental for solving quadratic equations and polynomial expressions.
What are common methods of factorisation?
Common methods include factoring out the greatest common factor (GCF), grouping terms, using special products (like the difference of squares and perfect squares), and factorising quadratics using various techniques.
How do you factorise a polynomial expression?
To factorise a polynomial, first identify and factor out the GCF if possible. Next, group terms with common factors and use methods like splitting the middle term or applying special factorisation formulas.
What is the greatest common factor (GCF)?
The GCF is the largest factor that is common to all terms in the expression. It is used to simplify the expression by dividing each term by the GCF and then factoring it out.
CBSE Class 8 Maths Notes Chapter 12 Factorisation PDF Download
Here we have provided CBSE Class 8 Maths Notes Chapter 12 Factorisation for the ease of students so that they can prepare better for their exams.
Ananya Gupta28 Aug, 2024
Share
CBSE Class 8 Maths Notes Chapter 12:
CBSE Class 8 Maths Notes Chapter 12 Factorisation introduces students to the process of breaking down algebraic expressions into simpler, more manageable components known as factors.
This chapter helps students understand how to identify and extract common factors, as well as how to factorise quadratic expressions and polynomials. By mastering these techniques, students can simplify mathematical problems, making them easier to solve.
These notes are designed to make the process of factorisation clear and accessible, helping students build a solid foundation for more advanced mathematical studies.
CBSE Class 8 Maths Notes Chapter 12 Factorisation Overview
These notes on CBSE Class 8 Maths Chapter 12 Factorisation have been prepared by subject experts of Physics Wallah. They provide a comprehensive overview of the chapter, covering essential concepts and methods to help students master the art of factorisation.
The notes simplify complex topics making it easier for students to understand how to break down algebraic expressions into factors. With clear explanations and practical examples these notes are an invaluable resource for students aiming to strengthen their foundation in mathematics.
CBSE Class 8 Maths Notes Chapter 12 Factorisation
Here are the notes for Class 8 students which are important for understanding CBSE Class 8 Maths Chapter 12: Factorisation. These notes provide a clear explanation of key factorisation techniques and concepts helping students break down algebraic expressions into simpler factors.
Mastering these concepts will enhance problem-solving skills and build a strong foundation for more advanced mathematical topics.
What are Factors?
Factors are components of an expression that, when multiplied together, result in the original expression. In factorisation, an expression is broken down into these simpler parts, which can be algebraic expressions, variables, or numbers.
By identifying and multiplying these factors, we can reconstruct the original expression, making factorisation a key technique in simplifying and solving algebraic problems.
Division of a monomial by another monomial
Division of a monomial by another monomial:
i) Division of 9x
2
by 3:
9x
2
÷ 3 = 3(3x
2
) / 3 = 3x
2
ii) Division of 6x
2
y by 2y:
6x
2
y÷2y = (6x
2
)y / 2y = 2y(3x
2
) / 2y = 3x
2
Long division method is used to divide a polynomial by a polynomial.
Example: Division of 3x
2
+ 3x – 5 by (x – 1) is shown below: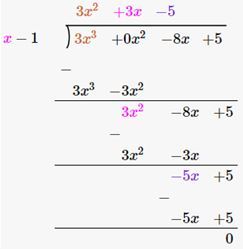
Factors of natural numbers
Every number can be expressed as a product of its prime factors, which is known as its prime factor form.
Example: Prime factor form of 42 is2 x 3 x 7, where 2, 3 and 7 are factors of 42.
Algebraic expressions
An algebraic expression is a mathematical phrase that includes variables, numbers, and operations such as addition, subtraction, multiplication, or division. Unlike constants, the values in an algebraic expression can vary depending on the values assigned to the variables.
For example: x + 1, p – q, 3x, 2x+3y, 5a/6b etc.
Factors of algebraic expressions and Factorisation
In algebra, a factor of an expression is a component that, when multiplied with other factors, gives the original expression. An irreducible factor is a factor that cannot be broken down any further into simpler components.
When factorising algebraic expressions, the goal is to express them in terms of these irreducible factors. This process simplifies the expression, making it easier to work with and solve. By identifying and using irreducible factors, you can rewrite algebraic expressions in their most simplified form.
Factorisation by common factors
To factorise an algebraic expression, the first step is to identify the highest common factor (HCF) among the terms. The HCF is the largest factor that divides all the terms of the expression. By factoring out this common factor, you can simplify the expression and express it as a product of simpler factors. This process makes it easier to handle and solve algebraic equations.
Example: Algebraic expression -2y
2
+ 8y can be written as 2y(-y+4), where 2y is the highest common factor in the expression.
Factorisation by regrouping terms
In cases where an algebraic expression does not have a common factor across all its terms, the factorisation process involves grouping terms that share common factors. By arranging the expression into groups where each group has a common factor, you can factor out the greatest common divisor from each group.
This approach simplifies the expression and often leads to further factorisation, breaking down the expression into more manageable parts. Grouping is a useful technique when dealing with complex algebraic expressions that do not lend themselves to straightforward factorisation.
Example:
= 12a + n – na – 12
= 12a-12+n-na
= 12(a-1)-n(a-1)
= (12-n)(a-1)
(12-n) and (a-1)are factors of the expression 12a+n-na-12
Method of Identities
Algebraic identities
The
algebraic equations
which are true for all values of variables in them are called algebraic identities.
Some of the identities are,
(a+b)
2
= a
2
+ 2ab + b
2
(a-b)
2
= a
2
– 2ab + b
2
(a+b)(a-b)= a
2
– b
2
Factorisation using algebraic identities
Algebraic identities can be used for factorisation
Example: (i)9x
2
+ 12xy + 4y
2
= ( 3x)
2
+ 2 x 3x x 2y+(2y)
2
= (3x+4y)
2
(ii)4a
2
– b
2
= (2a-b)(2a+b)
Visualisation of factorisation
The algebraic expression x
2
+ 8x + 16 can be written as (x+4)
2
. This can be visualised as shown below: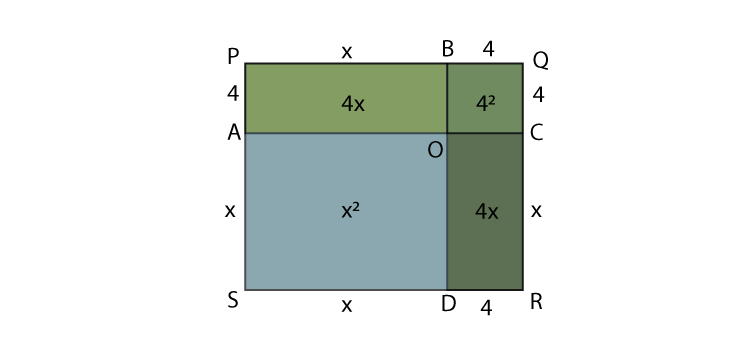
CBSE Class 8 Maths Notes Chapter 12 PDF Download
The PDF link for CBSE Class 8 Maths Notes Chapter 12 Factorisation is available below. These notes provide a thorough understanding of factorisation guiding students through various methods and techniques with clear examples.
Whether you're looking to revise key concepts or strengthen your problem-solving skills this PDF is a valuable resource for mastering factorisation. Download the PDF and ensure you're well-prepared for your exams.
Benefits of CBSE Class 8 Maths Notes Chapter 12 Factorisation
Enhanced Understanding of Concepts:
The notes provide a clear explanation of factorisation techniques, helping students grasp the fundamental concepts of breaking down algebraic expressions.
Simplified Learning:
Complex factorisation methods are presented in a simplified manner, making it easier for students to learn and apply these techniques effectively.
Improved Problem-Solving Skills:
With detailed examples and step-by-step solutions students can practice and improve their problem-solving abilities in algebraic expressions.
Foundation for Advanced Topics:
Mastering factorisation in Class 8 sets a solid foundation for more advanced algebraic concepts encountered in higher classes.
Comprehensive Coverage:
All essential topics within the chapter are covered thoroughly ensuring students have a complete understanding of factorisation.
Structured Learning:
The organized format of the notes facilitates structured learning allowing students to follow along easily and build their knowledge progressively.
Increased Confidence:
By practicing the techniques outlined in the notes students can gain confidence in their ability to handle algebraic expressions and solve related problems.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
