
KINETIC ENERGY
Work, Power and Energy of Class 9
KINETIC ENERGY
Energy of a body due to its motion is known as the kinetic energy of the body. If a body of mass m is moving with velocity v, then its kinetic energy =
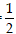 mv
2
.
mv
2
.
Examples :
- A speeding car
- A rolling stone
- A running athlete
- A flying air craft
Derivation of Kinetic Energy:
Let us now express the kinetic energy of an object in the form of an equation. Consider an object of mass, ‘m’ moving with a uniform velocity u on a perfectly frictionless surface.

Let it now be displaced through a distance s when a constant force, F acts on it, in the direction of its displacement.
So, work done = F × s … (i)
The work done on the object will cause a change in its velocity. Let its velocity change from u to v.
Let, a be the acceleration produced.
The relation connecting the initial velocity (u) and final velocity (v) of an object moving with a uniform acceleration (a) and the displacement (s) is
v 2 – u 2 = 2 as
This gives,
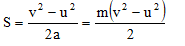 …(ii)
…(ii)
We know, F = m × a or
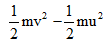 …(iii)
…(iii)
So, putting the values of ‘s’ and ‘F’ in equation (i)
W = m × a×
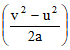
or
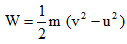
If the object is starting from its stationary position, that is u = 0, then,
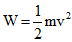
It is clear that the work done is equal to the change is the kinetic energy of an object.
If u=0 ,the work done will be
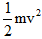
Thus, kinetic energy possessed by an object of mass m and moving with a uniform velocity, v is
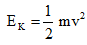
From this formula, it is clear that :
- The kinetic energy of a body is directly proportional to the mass of the body.
- The kinetic energy of a body is directly proportional to the square of velocity of the body.
Things to remember :
-
If the mass of a body is doubled, its kinetic energy also gets doubled and if the mass of a body is halved, its kinetic energy also gets halved. If the velocity of a body is doubled, its kinetic energy becomes 4 times. If the velocity of a body is halved, then its kinetic energy becomes 1/4
th
.
- Since the kinetic energy of a body depends on its mass and velocity, therefore heavy bodies moving with high velocities have more kinetic energy, than slow moving bodies of small mass.
Question 4. What is the work to be done to increase the velocity of a car from 30 km/h to 60 km/h. If mass of the car is 1500 kg.
Solution: Mass of car, m = 1500 kg.
Initial velocity, u = 30 km/h = 8.33 m/s.
Final velocity, v = 60 km/h = 16.67 m/s.
Work done,
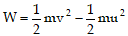
W =
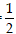 × 1500[(16.67)
2
- (8.33)
2
]
× 1500[(16.67)
2
- (8.33)
2
]
= 750(277.9 - 69.4)
W = 750 × 208.5 = 156375 J.
W = 1.56 × 10 5 J.
Question.5. Calculate the kinetic energy of a body of mass 2 kg moving with a velocity of 0.1 m/s.
Solution:
kinetic energy
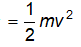
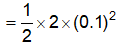
= 0.01 J
Question 6. An object of mass 15 kg is moving with a uniform velocity of 4 m/s. What is the kinetic energy possessed by the object?
Solution:
m = 15 kg
v = 4 m/s
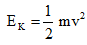
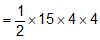
= 120 J





