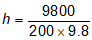POTENTIAL ENERGY
Work, Power and Energy of Class 9
If we lifts a football from the ground and place it on the top of a table, some work is done on the ball. Now, if this football falls down from the top of the table and let it hits another football lying on the ground, then the football lying on the ground in displaced from its original position. From this simple activity we canunderstand that a falling football is able to do work.
“We know, anything capable of doing work possess energy.” Therefore a football placed on the table also possess energy. This energy of the football lying on the top of the table is known as potential energy. Now the first question arises that from where this potential energy came in the football lying on the top of the table. Initially the work done by the child to rises the ball to the top of table from the ground the stored as energy. This stored energy is known as potential energy.
Definition of Potential Energy :
It is the energy possessed by the body due to its position or configuration. Configuration means the change in relative position of its parts or condition.
(i) Potential energy due to position : A body lying in an elevated position such as a stone lying on the roof of a building or water stored in a reservoir has got some potential energy. When allowed to fall, it is capable of doing some work. If it were raised higher, it could do more work and hence would have possessed more potential energy.
These are the examples of potential energy possessed by a body due to its position. This type of potential energyis also called gravitational potential energy.
(ii) Potential energy due to configuration or elastic potential energy or strain potential energy : Elastic potential energy is due to a change in the shape of the body.
The change in shape of a body can be brought about by compressing, stretching, bending or twisting.
(b) We can see more examples as :
- Water stored in dam has potential energy due to its position.
- A stone lying on the top of all hill or a mountain has potential energy due to its position.
- A stretched or compressed spring has potential energy due to this shape. When spring is stretched or compressed, work is done on it. This work done is stored as potential energy of the stretched or compressed spring.
- A wound spring of a watch has potential energy due to its shape.
- A stretched bow and arrow has potential energy due to its shape.
Some work has to be done to change the shape of a body (temporarily). This work gets stored is the deformed body in the form of elastic potential energy. When this deformed body is released it comes back to its original shape and size and the potential energy is given out in some other form. For example a wound up circular spring possesses elastic potential energy which drives a windup toy.
When we wind up the spring of a toy car using a winding key, then some work is done by us due to which the spring gets coiled more tightly. The work done in winding the spring gets stored up in the tightly coiled up spring in the form of elastic potential energy. When the wound up spring is slowly released, its potential energy is gradually converted into kinetic energy which turns the wheels of the toy car and makes it run.
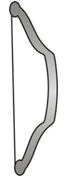
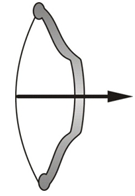
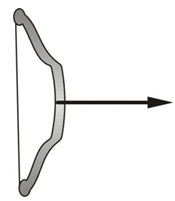
(b) A stretched bow possesses potential energy due to the relative position of different parts. When bow is pulled from position A to position B the energy spent in pulling the bow is converted into strain potential energy of the bow. This energy given is converted into kinetic energy when it is released (position C).
(A) (B) (C)
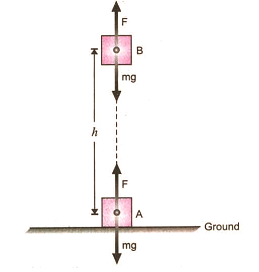
Potential energy of an object at a height
An object increases its energy when raised through a height. This is because work is done on it against gravity while it is being raised. The energy present in such an object is the gravitational potential energy.
The gravitational potential energy of an object at a point above the ground is defined as the work done in raising it from the ground to that point against gravity.
To arrive at an expression for the gravitational potential energy of an object at a height, consider a object of mass, m. Let it be raised through a height, h from the ground. A force is required to do this. The minimum force required to raise the object is equal to the weight of the object, mg.
The object gains energy equal to the work done on it. Let the work done on the object against gravity be. That is,
Work done, W = force x displacement
= mg×h
= m g h
Since work done on the object is equal to mgh,an energy equal to mgh units is gained by the object. This is the potential energy (Ep) of the object.
Ep = mgh
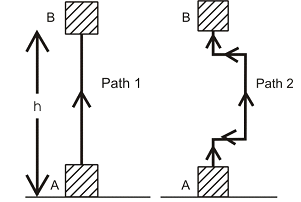
It is useful to note that the work done by gravity depends on the difference in vertical heights of the initial and final position of the object and not on the path along which the object moved. Figure below shows a case where a block is raised from position A to B by taking two different paths. Let the height, AB = h. In both the situations the work done on the object is mgh.
The potential energy of an object at a height depends on the ground level or the zero level you choose. An object in a given position can have a certain potential energy with respect to one level and a different value of potential energy with respect to another level.
Expression for Potential Energy of A body at a Certain Height:
The energy possessed by a body due to its position in the gravitational field of the earth is called gravitational potential energy.
Consider a block of mass m which is to be raised to a height ‘h’. The force required to lift the block must be equal to the gravitational force (i.e. weight of the block). Thus, Fg = mg. Let the applied force on the block be F = mg and the block is raised to the height h as shown in the figure.
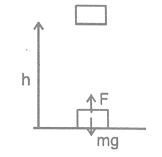
Work done by the applied force F is given by
W =
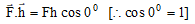
or W = Fh = mgh
Now, work done by the gravitational force on the block,
W =
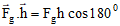
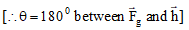
or
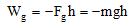
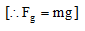
Work done against the gravitational force on the block is known as gravitational potential energy.
Ug= -(mgh) = mgh
Things to remember :
- Gravitational potential energy of a body on the surface of the earth (i.e. h = 0) is zero.
- Gravitational potential energy of a body increases if the body moves upward (i.e. h increases).
- Gravitational potential energy of a body deceases if the body moves downward (i.e. decreases).
- Gravitational potential energy depends only on the initial and final position of the body and not on the path followed by the body to go form initial position to final position. It means, the gravitational potential energy of body at height h will be same if it is either taken straight upward to height h or it is taken along a curved path to height h.
Question 7. Find the energy possessed by an object of mass 10 kg when it is at a height of 6 m above the ground given (g = 9.8 m/s 2 ).
Solution: m = 10 kg
h = 6m
g = 9.8 m/s 2
Potential energy = m × g × h = 588 J
Question 8. An object of mass 12 kg is at a certain height above the ground. If the potential energy of the object is 480 J, find the height at which the object is with respect to the ground. (g = 10 m/s 2 )
Solution: m = 12 kg
Ep= 480 J
Ep = m×g×h
480 J = 12 × 10 ×h
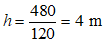
Question 9. A bag of wheat weighs 200 kg. To what height should it be raised so that its potential energy may be 9800 J? (g = 9.8 m/s)
Solution:
potential energy = 9800 J
m = 200 kg
g = 9.8 m/s
h = ?
potential energy = m ×g×h
9800 = 200 × 9.8 ×h