
NCERT Solutions for Class 8 Maths Chapter 3: NCERT Solutions for Class 8 Maths Chapter 3, "Understanding Quadrilaterals," help students learn about different types of quadrilaterals, like parallelograms, rhombuses, rectangles, and squares.
These solutions explain the properties of each shape with clear steps and diagrams, making it easy to understand. By using these solutions, students can improve their problem-solving skills and get better at identifying and analyzing quadrilaterals. These solutions are great for studying for exams and building a solid foundation in geometry.NCERT Solutions for Class 8 Maths Chapter 3 Overview
These solutions, prepared by subject experts of Physics Wallah, cover NCERT Solutions for Class 8 Maths Chapter 3, "Understanding Quadrilaterals." This chapter helps students learn about different types of quadrilaterals, such as parallelograms, rhombuses, rectangles, and squares, along with their properties. The solutions provide clear explanations and detailed diagrams to make the concepts easy to understand. By using these solutions, students can enhance their problem-solving skills and gain confidence in identifying and analyzing various quadrilaterals. These expertly prepared solutions are a valuable resource for exam preparation and building a strong foundation in geometry.NCERT Solutions for Class 8 Maths Chapter 3 PDF
The PDF link below has NCERT Solutions for Class 8 Maths Chapter 3, "Understanding Quadrilaterals." The explanations are clear and include step-by-step instructions and detailed diagrams to help you understand easily. This PDF is a helpful resource for improving your problem-solving skills, preparing for exams, and building a strong foundation in geometry.NCERT Solutions for Class 8 Maths Chapter 3 PDF
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals
Here we have provided NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals for the ease of students so that they can prepare better for their exams.NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.1 Page: 41
1. Given here are some figures.

Classify each of them on the basis of the following.
Simple curve (b) Simple closed curve (c) Polygon
(d) Convex polygon (e) Concave polygon
Solution: a) Simple curve: 1, 2, 5, 6 and 7 b) Simple closed curve: 1, 2, 5, 6 and 7 c) Polygon: 1 and 2 d) Convex polygon: 2 e) Concave polygon: 12. How many diagonals does each of the following have?
a) A convex quadrilateral (b) A regular hexagon (c) A triangle
Solution: a) A convex quadrilateral: 2. b) A regular hexagon: 9.
b) A regular hexagon: 9.
 c) A triangle: 0
c) A triangle: 0

3. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
Solution: Let ABCD be a convex quadrilateral.
From the figure, we infer that the quadrilateral ABCD is formed by two triangles,
i.e. ΔADC and ΔABC.
Since we know that sum of the interior angles of a triangle is 180°,
the sum of the measures of the angles is 180° + 180° = 360°
Let ABCD be a convex quadrilateral.
From the figure, we infer that the quadrilateral ABCD is formed by two triangles,
i.e. ΔADC and ΔABC.
Since we know that sum of the interior angles of a triangle is 180°,
the sum of the measures of the angles is 180° + 180° = 360°
 Let us take another quadrilateral ABCD which is not convex .
Join BC, such that it divides ABCD into two triangles ΔABC and ΔBCD. In ΔABC,
∠1 + ∠2 + ∠3 = 180° (angle sum property of triangle)
In ΔBCD,
∠4 + ∠5 + ∠6 = 180° (angle sum property of triangle)
∴, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 180° + 180°
⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
Thus, this property holds if the quadrilateral is not convex.
Let us take another quadrilateral ABCD which is not convex .
Join BC, such that it divides ABCD into two triangles ΔABC and ΔBCD. In ΔABC,
∠1 + ∠2 + ∠3 = 180° (angle sum property of triangle)
In ΔBCD,
∠4 + ∠5 + ∠6 = 180° (angle sum property of triangle)
∴, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 180° + 180°
⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
Thus, this property holds if the quadrilateral is not convex.
4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

What can you say about the angle sum of a convex polygon with number of sides? (a) 7 (b) 8 (c) 10 (d) n
Solution: The angle sum of a polygon having side n = (n-2)×180° a) 7 Here, n = 7 Thus, angle sum = (7-2)×180° = 5×180° = 900° b) 8 Here, n = 8 Thus, angle sum = (8-2)×180° = 6×180° = 1080° c) 10 Here, n = 10 Thus, angle sum = (10-2)×180° = 8×180° = 1440° d) n Here, n = n Thus, angle sum = (n-2)×180°5. What is a regular polygon?
State the name of a regular polygon of
(i) 3 sides (ii) 4 sides (iii) 6 sides
Solution: Regular polygon: A polygon having sides of equal length and angles of equal measures is called a regular polygon. A regular polygon is both equilateral and equiangular. (i) A regular polygon of 3 sides is called an equilateral triangle. (ii) A regular polygon of 4 sides is called a square. (iii) A regular polygon of 6 sides is called a regular hexagon.6. Find the angle measure of x in the following figures.
 Solution:
a) The figure has 4 sides. Hence, it is a quadrilateral. Sum of angles of the quadrilateral = 360°
⇒ 50° + 130° + 120° + x = 360°
⇒ 300° + x = 360°
⇒ x = 360° – 300° = 60°
b) The figure has 4 sides. Hence, it is a quadrilateral. Also, one side is perpendicular forming a right angle.
Sum of angles of the quadrilateral = 360°
⇒ 90° + 70° + 60° + x = 360°
⇒ 220° + x = 360°
⇒ x = 360° – 220° = 140°
c) The figure has 5 sides. Hence, it is a pentagon.
Solution:
a) The figure has 4 sides. Hence, it is a quadrilateral. Sum of angles of the quadrilateral = 360°
⇒ 50° + 130° + 120° + x = 360°
⇒ 300° + x = 360°
⇒ x = 360° – 300° = 60°
b) The figure has 4 sides. Hence, it is a quadrilateral. Also, one side is perpendicular forming a right angle.
Sum of angles of the quadrilateral = 360°
⇒ 90° + 70° + 60° + x = 360°
⇒ 220° + x = 360°
⇒ x = 360° – 220° = 140°
c) The figure has 5 sides. Hence, it is a pentagon.
 Sum of angles of the pentagon = 540° Two angles at the bottom are a linear pair.
∴, 180° – 70° = 110°
180° – 60° = 120°
⇒ 30° + 110° + 120° + x + x = 540°
⇒ 260° + 2x = 540°
⇒ 2x = 540° – 260° = 280°
⇒ 2x = 280°
= 140°
d) The figure has 5 equal sides. Hence, it is a regular pentagon. Thus, all its angles are equal.
5x = 540°
⇒ x = 540°/5
⇒ x = 108°
Sum of angles of the pentagon = 540° Two angles at the bottom are a linear pair.
∴, 180° – 70° = 110°
180° – 60° = 120°
⇒ 30° + 110° + 120° + x + x = 540°
⇒ 260° + 2x = 540°
⇒ 2x = 540° – 260° = 280°
⇒ 2x = 280°
= 140°
d) The figure has 5 equal sides. Hence, it is a regular pentagon. Thus, all its angles are equal.
5x = 540°
⇒ x = 540°/5
⇒ x = 108°
7.
 Solution:
a) Sum of all angles of triangle = 180°
One side of triangle = 180°- (90° + 30°) = 60°
x + 90° = 180° ⇒ x = 180° – 90° = 90°
y + 60° = 180° ⇒ y = 180° – 60° = 120°
z + 30° = 180° ⇒ z = 180° – 30° = 150°
x + y + z = 90° + 120° + 150° = 360°
b) Sum of all angles of quadrilateral = 360°
One side of quadrilateral = 360°- (60° + 80° + 120°) = 360° – 260° = 100°
x + 120° = 180° ⇒ x = 180° – 120° = 60°
y + 80° = 180° ⇒ y = 180° – 80° = 100°
z + 60° = 180° ⇒ z = 180° – 60° = 120°
w + 100° = 180° ⇒ w = 180° – 100° = 80°
x + y + z + w = 60° + 100° + 120° + 80° = 360°
Solution:
a) Sum of all angles of triangle = 180°
One side of triangle = 180°- (90° + 30°) = 60°
x + 90° = 180° ⇒ x = 180° – 90° = 90°
y + 60° = 180° ⇒ y = 180° – 60° = 120°
z + 30° = 180° ⇒ z = 180° – 30° = 150°
x + y + z = 90° + 120° + 150° = 360°
b) Sum of all angles of quadrilateral = 360°
One side of quadrilateral = 360°- (60° + 80° + 120°) = 360° – 260° = 100°
x + 120° = 180° ⇒ x = 180° – 120° = 60°
y + 80° = 180° ⇒ y = 180° – 80° = 100°
z + 60° = 180° ⇒ z = 180° – 60° = 120°
w + 100° = 180° ⇒ w = 180° – 100° = 80°
x + y + z + w = 60° + 100° + 120° + 80° = 360°
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.2 Page: 44
1. Find x in the following figures.
 Solution:
a)
Solution:
a)
 125° + m = 180° ⇒ m = 180° – 125° = 55° (Linear pair)
125° + n = 180° ⇒ n = 180° – 125° = 55° (Linear pair)
x = m + n (The exterior angle of a triangle is equal to the sum of the two opposite interior angles)
⇒ x = 55° + 55° = 110°
b)
125° + m = 180° ⇒ m = 180° – 125° = 55° (Linear pair)
125° + n = 180° ⇒ n = 180° – 125° = 55° (Linear pair)
x = m + n (The exterior angle of a triangle is equal to the sum of the two opposite interior angles)
⇒ x = 55° + 55° = 110°
b)
 Two interior angles are right angles = 90°
70° + m = 180° ⇒ m = 180° – 70° = 110° (Linear pair)
60° + n = 180° ⇒ n = 180° – 60° = 120° (Linear pair) The figure is having five sides and is a pentagon.
Thus, sum of the angles of a pentagon = 540°
⇒ 90° + 90° + 110° + 120° + y = 540°
⇒ 410° + y = 540° ⇒ y = 540° – 410° = 130°
x + y = 180° (Linear pair)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
Two interior angles are right angles = 90°
70° + m = 180° ⇒ m = 180° – 70° = 110° (Linear pair)
60° + n = 180° ⇒ n = 180° – 60° = 120° (Linear pair) The figure is having five sides and is a pentagon.
Thus, sum of the angles of a pentagon = 540°
⇒ 90° + 90° + 110° + 120° + y = 540°
⇒ 410° + y = 540° ⇒ y = 540° – 410° = 130°
x + y = 180° (Linear pair)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
2. Find the measure of each exterior angle of a regular polygon of
(i) 9 sides (ii) 15 sides
Solution: Sum of the angles of a regular polygon having side n = (n-2)×180° (i) Sum of the angles of a regular polygon having 9 sides = (9-2)×180°= 7×180° = 1260° Each interior angle=1260/9 = 140° Each exterior angle = 180° – 140° = 40° Or, Each exterior angle = Sum of exterior angles/Number of angles = 360/9 = 40° (ii) Sum of angles of a regular polygon having side 15 = (15-2)×180° = 13×180° = 2340° Each interior angle = 2340/15 = 156° Each exterior angle = 180° – 156° = 24° Or, Each exterior angle = sum of exterior angles/Number of angles = 360/15 = 24°3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Solution: Each exterior angle = sum of exterior angles/Number of angles 24°= 360/ Number of sides ⇒ Number of sides = 360/24 = 15 Thus, the regular polygon has 15 sides.4. How many sides does a regular polygon have if each of its interior angles is 165°?
Solution: Interior angle = 165° Exterior angle = 180° – 165° = 15° Number of sides = sum of exterior angles/exterior angles ⇒ Number of sides = 360/15 = 24 Thus, the regular polygon has 24 sides.5. a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
b) Can it be an interior angle of a regular polygon? Why?
Solution: a) Exterior angle = 22° Number of sides = sum of exterior angles/ exterior angle ⇒ Number of sides = 360/22 = 16.36 No, we can’t have a regular polygon with each exterior angle as 22° as it is not a divisor of 360. b) Interior angle = 22° Exterior angle = 180° – 22°= 158° No, we can’t have a regular polygon with each exterior angle as 158° as it is not a divisor of 360.6. a) What is the minimum interior angle possible for a regular polygon? Why?
b) What is the maximum exterior angle possible for a regular polygon?
Solution: a) An equilateral triangle is the regular polygon (with 3 sides) having the least possible minimum interior angle because a regular polygon can be constructed with minimum 3 sides. Since the sum of interior angles of a triangle = 180° Each interior angle = 180/3 = 60° b) An equilateral triangle is the regular polygon (with 3 sides) having the maximum exterior angle because the regular polygon with the least number of sides has the maximum exterior angle possible. Maximum exterior possible = 180 – 60° = 120°NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.3 Page: 50
1. Given a parallelogram ABCD. Complete each statement along with the definition or property used.
 (i) AD = …… (ii) ∠DCB = ……
(iii) OC = …… (iv) m ∠DAB + m ∠CDA = ……
Solution:
(i) AD = BC (Opposite sides of a parallelogram are equal)
(ii) ∠DCB = ∠DAB (Opposite angles of a parallelogram are equal)
(iii) OC = OA (Diagonals of a parallelogram are equal)
(iv) m ∠DAB + m ∠CDA = 180°
(i) AD = …… (ii) ∠DCB = ……
(iii) OC = …… (iv) m ∠DAB + m ∠CDA = ……
Solution:
(i) AD = BC (Opposite sides of a parallelogram are equal)
(ii) ∠DCB = ∠DAB (Opposite angles of a parallelogram are equal)
(iii) OC = OA (Diagonals of a parallelogram are equal)
(iv) m ∠DAB + m ∠CDA = 180°
2. Consider the following parallelograms. Find the values of the unknown x, y, z
 Solution:
(i)
Solution:
(i)
 y = 100° (opposite angles of a parallelogram)
x + 100° = 180° (adjacent angles of a parallelogram)
⇒ x = 180° – 100° = 80°
x = z = 80° (opposite angles of a parallelogram)
∴, x = 80°, y = 100° and z = 80°
y = 100° (opposite angles of a parallelogram)
x + 100° = 180° (adjacent angles of a parallelogram)
⇒ x = 180° – 100° = 80°
x = z = 80° (opposite angles of a parallelogram)
∴, x = 80°, y = 100° and z = 80°
 (ii)
50° + x = 180° ⇒ x = 180° – 50° = 130° (adjacent angles of a parallelogram) x = y = 130° (opposite angles of a parallelogram)
x = z = 130° (corresponding angle)
(iii)
(ii)
50° + x = 180° ⇒ x = 180° – 50° = 130° (adjacent angles of a parallelogram) x = y = 130° (opposite angles of a parallelogram)
x = z = 130° (corresponding angle)
(iii)
 x = 90° (vertical opposite angles)
x + y + 30° = 180° (angle sum property of a triangle)
⇒ 90° + y + 30° = 180°
⇒ y = 180° – 120° = 60°
also, y = z = 60° (alternate angles)
(iv)
x = 90° (vertical opposite angles)
x + y + 30° = 180° (angle sum property of a triangle)
⇒ 90° + y + 30° = 180°
⇒ y = 180° – 120° = 60°
also, y = z = 60° (alternate angles)
(iv)
 z = 80° (corresponding angle) z = y = 80° (alternate angles) x + y = 180° (adjacent angles)
⇒ x + 80° = 180° ⇒ x = 180° – 80° = 100°
(v)
z = 80° (corresponding angle) z = y = 80° (alternate angles) x + y = 180° (adjacent angles)
⇒ x + 80° = 180° ⇒ x = 180° – 80° = 100°
(v)
 x=28o
y = 112o z = 28o
x=28o
y = 112o z = 28o
3. Can a quadrilateral ABCD be a parallelogram if (i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii)∠A = 70° and ∠C = 65°?
Solution: (i) Yes, a quadrilateral ABCD can be a parallelogram if ∠D + ∠B = 180° but it should also fulfil some conditions, which are: (a) The sum of the adjacent angles should be 180°. (b) Opposite angles must be equal. (ii) No, opposite sides should be of the same length. Here, AD ≠ BC (iii) No, opposite angles should be of the same measures. ∠A ≠ ∠C4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Solution: ABCD is a figure of quadrilateral that is not a parallelogram but has exactly two opposite angles, that is, ∠B = ∠D of equal measure. It is not a parallelogram because ∠A ≠ ∠C.
ABCD is a figure of quadrilateral that is not a parallelogram but has exactly two opposite angles, that is, ∠B = ∠D of equal measure. It is not a parallelogram because ∠A ≠ ∠C.
5. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Solution: Let the measures of two adjacent angles ∠A and ∠B be 3x and 2x, respectively in parallelogram ABCD. ∠A + ∠B = 180° ⇒ 3x + 2x = 180° ⇒ 5x = 180° ⇒ x = 36° We know that opposite sides of a parallelogram are equal. ∠A = ∠C = 3x = 3 × 36° = 108° ∠B = ∠D = 2x = 2 × 36° = 72°6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Solution: Let ABCD be a parallelogram. Sum of adjacent angles of a parallelogram = 180° ∠A + ∠B = 180° ⇒ 2∠A = 180° ⇒ ∠A = 90° also, 90° + ∠B = 180° ⇒ ∠B = 180° – 90° = 90° ∠A = ∠C = 90° ∠B = ∠D = 907. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
 Solution:
y = 40° (alternate interior angle)
∠P = 70° (alternate interior angle)
∠P = ∠H = 70° (opposite angles of a parallelogram)
z = ∠H – 40°= 70° – 40° = 30°
∠H + x = 180°
⇒ 70° + x = 180°
⇒ x = 180° – 70° = 110°
Solution:
y = 40° (alternate interior angle)
∠P = 70° (alternate interior angle)
∠P = ∠H = 70° (opposite angles of a parallelogram)
z = ∠H – 40°= 70° – 40° = 30°
∠H + x = 180°
⇒ 70° + x = 180°
⇒ x = 180° – 70° = 110°
8. The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
 Solution:
(i) SG = NU and SN = GU (opposite sides of a parallelogram are equal) 3x = 18
x = 18/3
⇒ x =6
3y – 1 = 26
⇒ 3y = 26 + 1
⇒ y = 27/3=9
x = 6 and y = 9
(ii) 20 = y + 7 and 16 = x + y (diagonals of a parallelogram bisect each other) y + 7 = 20
⇒ y = 20 – 7 = 13 and,
x + y = 16
⇒ x + 13 = 16
⇒ x = 16 – 13 = 3
x = 3 and y = 13
Solution:
(i) SG = NU and SN = GU (opposite sides of a parallelogram are equal) 3x = 18
x = 18/3
⇒ x =6
3y – 1 = 26
⇒ 3y = 26 + 1
⇒ y = 27/3=9
x = 6 and y = 9
(ii) 20 = y + 7 and 16 = x + y (diagonals of a parallelogram bisect each other) y + 7 = 20
⇒ y = 20 – 7 = 13 and,
x + y = 16
⇒ x + 13 = 16
⇒ x = 16 – 13 = 3
x = 3 and y = 13
9. In the above figure both RISK and CLUE are parallelograms. Find the value of x.
 Solution:
∠K + ∠R = 180° (adjacent angles of a parallelogram are supplementary)
⇒ 120° + ∠R = 180°
⇒ ∠R = 180° – 120° = 60°
also, ∠R = ∠SIL (corresponding angles)
⇒ ∠SIL = 60°
also, ∠ECR = ∠L = 70° (corresponding angles) x + 60° + 70° = 180° (angle sum of a triangle)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
Solution:
∠K + ∠R = 180° (adjacent angles of a parallelogram are supplementary)
⇒ 120° + ∠R = 180°
⇒ ∠R = 180° – 120° = 60°
also, ∠R = ∠SIL (corresponding angles)
⇒ ∠SIL = 60°
also, ∠ECR = ∠L = 70° (corresponding angles) x + 60° + 70° = 180° (angle sum of a triangle)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
10. Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
 Solution:
When a transversal line intersects two lines in such a way that the sum of the adjacent angles on the same side of transversal is 180°, then the lines are parallel to each other. Here, ∠M + ∠L = 100° + 80° = 180°
Thus, MN || LK
As the quadrilateral KLMN has one pair of parallel lines, it is a trapezium. MN and LK are parallel lines.
Solution:
When a transversal line intersects two lines in such a way that the sum of the adjacent angles on the same side of transversal is 180°, then the lines are parallel to each other. Here, ∠M + ∠L = 100° + 80° = 180°
Thus, MN || LK
As the quadrilateral KLMN has one pair of parallel lines, it is a trapezium. MN and LK are parallel lines.
11. Find m∠C in Fig 3.33 if AB || DC.

12. Find the measure of ∠P and ∠S if SP || RQ ? in Fig 3.34. (If you find m∠R, is there more than one method to find m∠P?)
 Solution:
∠P + ∠Q = 180° (angles on the same side of transversal)
⇒ ∠P + 130° = 180°
⇒ ∠P = 180° – 130° = 50°
also, ∠R + ∠S = 180° (angles on the same side of transversal)
⇒ 90° + ∠S = 180°
⇒ ∠S = 180° – 90° = 90°
Thus, ∠P = 50° and ∠S = 90°
Yes, there are more than one method to find m∠P.
PQRS is a quadrilateral. Sum of measures of all angles is 360°.
Since, we know the measurement of ∠Q, ∠R and ∠S.
∠Q = 130°, ∠R = 90° and ∠S = 90°
∠P + 130° + 90° + 90° = 360°
⇒ ∠P + 310° = 360°
⇒ ∠P = 360° – 310° = 50°
Solution:
∠P + ∠Q = 180° (angles on the same side of transversal)
⇒ ∠P + 130° = 180°
⇒ ∠P = 180° – 130° = 50°
also, ∠R + ∠S = 180° (angles on the same side of transversal)
⇒ 90° + ∠S = 180°
⇒ ∠S = 180° – 90° = 90°
Thus, ∠P = 50° and ∠S = 90°
Yes, there are more than one method to find m∠P.
PQRS is a quadrilateral. Sum of measures of all angles is 360°.
Since, we know the measurement of ∠Q, ∠R and ∠S.
∠Q = 130°, ∠R = 90° and ∠S = 90°
∠P + 130° + 90° + 90° = 360°
⇒ ∠P + 310° = 360°
⇒ ∠P = 360° – 310° = 50°
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.4 Page: 55
1. State whether True or False.
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All squares are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
Solution: (a) False Because all squares are rectangles but all rectangles are not squares. (b) True (c) True (d) False Because all squares are parallelograms as opposite sides are parallel and opposite angles are equal. (e) False. Because, for example, the length of the sides of a kite are not of the same length. (f) True (g) True (h) True2. Identify all the quadrilaterals that have.
(a) four sides of equal length (b) four right angles
Solution: (a) Rhombus and square have all four sides of equal length. (b) Square and rectangle have four right angles.3. Explain how a square is
(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle
Solution (i) Square is a quadrilateral because it has four sides. (ii) Square is a parallelogram because it’s opposite sides are parallel and opposite angles are equal. (iii) Square is a rhombus because all the four sides are of equal length and diagonals bisect at right angles. (iv)Square is a rectangle because each interior angle, of the square, is 90°4. Name the quadrilaterals whose diagonals.
(i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal
Solution (i) Parallelogram, Rhombus, Square and Rectangle (ii) Rhombus and Square (iii)Rectangle and Square5. Explain why a rectangle is a convex quadrilateral.
Solution A rectangle is a convex quadrilateral because both of its diagonals lie inside the rectangle.6. ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).
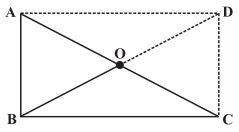 Solution
AD and DC are drawn so that AD || BC and AB || DC
AD = BC and AB = DC
ABCD is a rectangle as opposite sides are equal and parallel to each other and all the interior angles are of 90°.
In a rectangle, diagonals are of equal length and also bisect each other.
Hence, AO = OC = BO = OD
Thus, O is equidistant from A, B and C.
Solution
AD and DC are drawn so that AD || BC and AB || DC
AD = BC and AB = DC
ABCD is a rectangle as opposite sides are equal and parallel to each other and all the interior angles are of 90°.
In a rectangle, diagonals are of equal length and also bisect each other.
Hence, AO = OC = BO = OD
Thus, O is equidistant from A, B and C.
Benefits of NCERT Solutions for Class 8 Maths Chapter 3
- Clear Understanding : The solutions provide step-by-step explanations, helping students understand the properties and types of quadrilaterals thoroughly.
- Concept Reinforcement : By working through these solutions, students can reinforce their understanding of important concepts such as the angle sum property, properties of special quadrilaterals, and the characteristics of different types of quadrilaterals.
- Problem-Solving Skills : The solutions include various problems that enhance students' problem-solving skills, teaching them how to approach and solve different types of questions effectively.
- Exam Preparation : These solutions are aligned with the NCERT curriculum and help students prepare for exams by providing practice with a range of questions that are likely to appear in their tests.
- Self-Study Aid : The detailed explanations make these solutions an excellent resource for self-study, enabling students to learn at their own pace and clarify any doubts independently.
- Confidence Building : Regular practice with these solutions builds students' confidence in their mathematical abilities, ensuring they are well-prepared for both classroom assessments and standardized exams.
- Strong Foundation : Understanding quadrilaterals is a fundamental part of geometry, and mastering these concepts provides a strong foundation for more advanced mathematical studies in higher classes.
NCERT Solutions for Class 8 Maths Chapter 3 FAQs
What is a quadrilateral?
What are the types of quadrilaterals?
What is the angle sum property of a quadrilateral?
Why is understanding quadrilaterals important?
What are the diagonals of a quadrilateral?









